Bipyramid

"Dipyramid" redirects here. For the mountain, see Dipyramid (Alaska).

In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar and a bipyramid is usually symmetric, meaning the two pyramids are mirror images across their common base plane. When each apex (pl. apices, the off-base vertices) of the bipyramid is on a line perpendicular to the base and passing through its center, it is a right bipyramid;^[a] otherwise it is oblique. When the base is a regular polygon, the bipyramid is also called regular.

Definition and properties

The triangular bipyramid, square bipyramid, and pentagonal bipyramid.

A bipyramid is a polyhedron constructed by fusing two pyramids which share the same polygonal base;^[1] a pyramid is in turn constructed by connecting each vertex of its base to a single new vertex (the apex) not lying in the plane of the base, for an n-gonal base forming n triangular faces in addition to the base face. An n-gonal bipyramid thus has 2n faces, 3n edges, and n + 2 vertices. More generally, a right pyramid is a pyramid where the apices are on the perpendicular line through the centroid of an arbitrary polygon or the incenter of a tangential polygon, depending on the source.^[a] Likewise, a right bipyramid is a polyhedron constructed by attaching two symmetrical right bipyramid bases; bipyramids whose apices are not on this line are called oblique bipyramids.^[2]

When the two pyramids are mirror images, the bipyramid is called symmetric. It is called regular if its base is a regular polygon.^[1] When the base is a regular polygon and the apices are on the perpendicular line through its center (a regular right bipyramid) then all of its faces are isosceles triangles; sometimes the name bipyramid refers specifically to symmetric regular right bipyramids,^[3] Examples of such bipyramids are the triangular bipyramid, octahedron (square bipyramid) and pentagonal bipyramid. If all their edges are equal in length, these shapes consist of equilateral triangle faces, making them deltahedra;^[4][5] the triangular bipyramid and the pentagonal bipyramid are Johnson solids, and the regular octahedron is a Platonic solid.^[6]

The octahedron is dual to the cube

The symmetric regular right bipyramids have prismatic symmetry, with dihedral symmetry group D_nh of order 4n: they are unchanged when rotated ⁠1/n⁠ of a turn around the axis of symmetry, reflected across any plane passing through both apices and a base vertex or both apices and the center of a base edge, or reflected across the mirror plane.^[7] Because their faces are transitive under these symmetry transformations, they are isohedral.^[8][9] They are the dual polyhedra of prisms and the prisms are the dual of bipyramids as well; the bipyramids vertices correspond to the faces of the prism, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other, and vice versa.^[10] The prisms share the same symmetry as the bipyramids.^[11] The regular octahedron is more symmetric still, as its base vertices and apices are indistinguishable and can be exchanged by reflections or rotations; the regular octahedron and its dual, the cube, have octahedral symmetry.^[12]

The volume of a symmetric bipyramid is $${\displaystyle {\frac {2}{3}}Bh,}$$ where B is the area of the base and h the perpendicular distance from the base plane to either apex. In the case of a regular n-sided polygon with side length s and whose altitude is h, the volume of such a bipyramid is: $${\displaystyle {\frac {n}{6}}hs^{2}\cot {\frac {\pi }{n}}.}$$

Related and other types of bipyramid

A concave tetragonal bipyramid

An asymmetric hexagonal bipyramid

Concave bipyramids

A concave bipyramid has a concave polygon base, and one example is a concave tetragonal bipyramid or an irregular concave octahedron. A bipyramid with an arbitrary polygonal base could be considered a right bipyramid if the apices are on a line perpendicular to the base passing through the base's centroid.

Asymmetric bipyramids

An asymmetric bipyramid has apices which are not mirrored across the base plane; for a right bipyramid this only happens if each apex is a different distance from the base.

The dual of an asymmetric right n-gonal bipyramid is an n-gonal frustum.

A regular asymmetric right n-gonal bipyramid has symmetry group C_nv, of order 2n.

Scalene triangle bipyramids

Example: ditetragonal bipyramid (2n = 2×4)

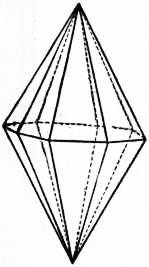
An isotoxal right (symmetric) di-n-gonal bipyramid is a right (symmetric) 2n-gonal bipyramid with an isotoxal flat polygon base: its 2n basal vertices are coplanar, but alternate in two radii.

All its faces are congruent scalene triangles, and it is isohedral. It can be seen as another type of a right symmetric di-n-gonal scalenohedron, with an isotoxal flat polygon base.

An isotoxal right (symmetric) di-n-gonal bipyramid has n two-fold rotation axes through opposite basal vertices, n reflection planes through opposite apical edges, an n-fold rotation axis through apices, a reflection plane through base, and an n-fold rotation-reflection axis through apices,^[13] representing symmetry group D_nh, [n,2], (*22n), of order 4n. (The reflection about the base plane corresponds to the 0° rotation-reflection. If n is even, then there is an inversion symmetry about the center, corresponding to the 180° rotation-reflection.)

Example with 2n = 2×3:

An isotoxal right (symmetric) ditrigonal bipyramid has three similar vertical planes of symmetry, intersecting in a (vertical) 3-fold rotation axis; perpendicular to them is a fourth plane of symmetry (horizontal); at the intersection of the three vertical planes with the horizontal plane are three similar (horizontal) 2-fold rotation axes; there is no center of inversion symmetry,^[14] but there is a center of symmetry: the intersection point of the four axes.

Example with 2n = 2×4:

An isotoxal right (symmetric) ditetragonal bipyramid has four vertical planes of symmetry of two kinds, intersecting in a (vertical) 4-fold rotation axis; perpendicular to them is a fifth plane of symmetry (horizontal); at the intersection of the four vertical planes with the horizontal plane are four (horizontal) 2-fold rotation axes of two kinds, each perpendicular to a plane of symmetry; two vertical planes bisect the angles between two horizontal axes; and there is a centre of inversion symmetry.^[15]

Double example:

• The bipyramid with isotoxal 2×2-gon base vertices U, U', V, V' and right symmetric apices A, A'$${\displaystyle {\begin{alignedat}{5}U&=(1,0,0),&\quad V&=(0,2,0),&\quad A&=(0,0,1),\\U'&=(-1,0,0),&\quad V'&=(0,-2,0),&\quad A'&=(0,0,-1),\end{alignedat}}}$$ has its faces isosceles. Indeed:
  • Upper apical edge lengths:$${\displaystyle {\begin{aligned}{\overline {AU}}&={\overline {AU'}}={\sqrt {2}}\,,\\[2pt]{\overline {AV}}&={\overline {AV'}}={\sqrt {5}}\,;\end{aligned}}}$$
  • Base edge lengths: $${\displaystyle {\overline {UV}}={\overline {VU'}}={\overline {U'V'}}={\overline {V'U}}={\sqrt {5}}\,;}$$
  • Lower apical edge lengths (equal to upper edge lengths):$${\displaystyle {\begin{aligned}{\overline {A'U}}&={\overline {A'U'}}={\sqrt {2}}\,,\\[2pt]{\overline {A'V}}&={\overline {A'V'}}={\sqrt {5}}\,.\end{aligned}}}$$

• The bipyramid with same base vertices, but with right symmetric apices $${\displaystyle {\begin{aligned}A&=(0,0,2),\\A'&=(0,0,-2),\end{aligned}}}$$ also has its faces isosceles. Indeed:
  • Upper apical edge lengths:$${\displaystyle {\begin{aligned}{\overline {AU}}&={\overline {AU'}}={\sqrt {5}}\,,\\[2pt]{\overline {AV}}&={\overline {AV'}}=2{\sqrt {2}}\,;\end{aligned}}}$$
  • Base edge length (equal to previous example): $${\displaystyle {\overline {UV}}={\overline {VU'}}={\overline {U'V'}}={\overline {V'U}}={\sqrt {5}}\,;}$$
  • Lower apical edge lengths (equal to upper edge lengths):$${\displaystyle {\begin{aligned}{\overline {A'U}}&={\overline {A'U'}}={\sqrt {5}}\,,\\[2pt]{\overline {A'V}}&={\overline {A'V'}}=2{\sqrt {2}}\,.\end{aligned}}}$$

Examples of rhombic bipyramids

In crystallography, isotoxal right (symmetric) didigonal^[b] (8-faced), ditrigonal (12-faced), ditetragonal (16-faced), and dihexagonal (24-faced) bipyramids exist.^[13][16]

Scalenohedra

Example: ditrigonal scalenohedron (2n = 2×3)

A scalenohedron is similar to a bipyramid; the difference is that the scalenohedra has a zig-zag pattern in the middle edges.^[17]

It has two apices and 2n basal vertices, 4n faces, and 6n edges; it is topologically identical to a 2n-gonal bipyramid, but its 2n basal vertices alternate in two rings above and below the center.^[16]

All its faces are congruent scalene triangles, and it is isohedral. It can be seen as another type of a right symmetric di-n-gonal bipyramid, with a regular zigzag skew polygon base.

A regular right symmetric di-n-gonal scalenohedron has n two-fold rotation axes through opposite basal mid-edges, n reflection planes through opposite apical edges, an n-fold rotation axis through apices, and a 2n-fold rotation-reflection axis through apices (about which 1n rotations-reflections globally preserve the solid),^[13] representing symmetry group D_nv = D_nd, [2⁺,2n], (2*n), of order 4n. (If n is odd, then there is an inversion symmetry about the center, corresponding to the 180° rotation-reflection.)

Example with 2n = 2×3:

A regular right symmetric ditrigonal scalenohedron has three similar vertical planes of symmetry inclined to one another at 60° and intersecting in a (vertical) 3-fold rotation axis, three similar horizontal 2-fold rotation axes, each perpendicular to a plane of symmetry, a center of inversion symmetry,^[18] and a vertical 6-fold rotation-reflection axis.

Example with 2n = 2×2:

A regular right symmetric didigonal scalenohedron has only one vertical and two horizontal 2-fold rotation axes, two vertical planes of symmetry, which bisect the angles between the horizontal pair of axes, and a vertical 4-fold rotation-reflection axis;^[19] it has no center of inversion symmetry.

Examples of disphenoids and of an 8-faced scalenohedron

For at most two particular values of ${\displaystyle z_{A}=|z_{A'}|,}$ the faces of such a scalenohedron may be isosceles.

Double example:

• The scalenohedron with regular zigzag skew 2×2-gon base vertices U, U', V, V' and right symmetric apices A, A'$${\displaystyle {\begin{alignedat}{5}U&=(3,0,2),&\quad V&=(0,3,-2),&\quad A&=(0,0,3),\\U'&=(-3,0,2),&\quad V'&=(0,-3,-2),&\quad A'&=(0,0,-3),\end{alignedat}}}$$ has its faces isosceles. Indeed:
  • Upper apical edge lengths:$${\displaystyle {\begin{aligned}{\overline {AU}}&={\overline {AU'}}={\sqrt {10}}\,,\\[2pt]{\overline {AV}}&={\overline {AV'}}={\sqrt {34}}\,;\end{aligned}}}$$
  • Base edge length:$${\displaystyle {\overline {UV}}={\overline {VU'}}={\overline {U'V'}}={\overline {V'U}}={\sqrt {34}}\,;}$$
  • Lower apical edge lengths (equal to upper edge lengths swapped):$${\displaystyle {\begin{aligned}{\overline {A'U}}&={\overline {A'U'}}={\sqrt {34}}\,,\\[2pt]{\overline {A'V}}&={\overline {A'V'}}={\sqrt {10}}\,.\end{aligned}}}$$

• The scalenohedron with same base vertices, but with right symmetric apices$${\displaystyle {\begin{aligned}A&=(0,0,7),\\A'&=(0,0,-7),\end{aligned}}}$$ also has its faces isosceles. Indeed:
  • Upper apical edge lengths:$${\displaystyle {\begin{aligned}{\overline {AU}}&={\overline {AU'}}={\sqrt {34}}\,,\\[2pt]{\overline {AV}}&={\overline {AV'}}=3{\sqrt {10}}\,;\end{aligned}}}$$
  • Base edge length (equal to previous example): $${\displaystyle {\overline {UV}}={\overline {VU'}}={\overline {U'V'}}={\overline {V'U}}={\sqrt {34}}\,;}$$
  • Lower apical edge lengths (equal to upper edge lengths swapped):$${\displaystyle {\begin{aligned}{\overline {A'U}}&={\overline {A'U'}}=3{\sqrt {10}}\,,\\[2pt]{\overline {A'V}}&={\overline {A'V'}}={\sqrt {34}}\,.\end{aligned}}}$$

In crystallography, regular right symmetric didigonal (8-faced) and ditrigonal (12-faced) scalenohedra exist.^[13][16]

The smallest geometric scalenohedra have eight faces, and are topologically identical to the regular octahedron. In this case (2n = 2×2), in crystallography, a regular right symmetric didigonal (8-faced) scalenohedron is called a tetragonal scalenohedron.^[13][16]

Let us temporarily focus on the regular right symmetric 8-faced scalenohedra with h = r, i.e. $${\displaystyle z_{A}=|z_{A'}|=x_{U}=|x_{U'}|=y_{V}=|y_{V'}|.}$$ Their two apices can be represented as A, A' and their four basal vertices as U, U', V, V': $${\displaystyle {\begin{alignedat}{5}U&=(1,0,z),&\quad V&=(0,1,-z),&\quad A&=(0,0,1),\\U'&=(-1,0,z),&\quad V'&=(0,-1,-z),&\quad A'&=(0,0,-1),\end{alignedat}}}$$ where z is a parameter between 0 and 1.

At z = 0, it is a regular octahedron; at z = 1, it has four pairs of coplanar faces, and merging these into four congruent isosceles triangles makes it a disphenoid; for z > 1, it is concave.

Example: geometric variations with regular right symmetric 8-faced scalenohedra:

z = 0.1	z = 0.25	z = 0.5	z = 0.95	z = 1.5

If the 2n-gon base is both isotoxal in-out and zigzag skew, then not all faces of the isotoxal right symmetric scalenohedron are congruent.

Example with five different edge lengths:

• The scalenohedron with isotoxal in-out zigzag skew 2×2-gon base vertices U, U', V, V' and right symmetric apices A, A' $${\displaystyle {\begin{alignedat}{5}U&=(1,0,1),&\quad V&=(0,2,-1),&\quad A&=(0,0,3),\\U'&=(-1,0,1),&\quad V'&=(0,-2,-1),&\quad A'&=(0,0,-3),\end{alignedat}}}$$ has congruent scalene upper faces, and congruent scalene lower faces, but not all its faces are congruent. Indeed:
  • Upper apical edge lengths:$${\displaystyle {\begin{aligned}{\overline {AU}}&={\overline {AU'}}={\sqrt {5}}\,,\\[2pt]{\overline {AV}}&={\overline {AV'}}=2{\sqrt {5}}\,;\end{aligned}}}$$
  • Base edge length:$${\displaystyle {\overline {UV}}={\overline {VU'}}={\overline {U'V'}}={\overline {V'U}}=3;}$$
  • Lower apical edge lengths:$${\displaystyle {\begin{aligned}{\overline {A'U}}&={\overline {A'U'}}={\sqrt {17}}\,,\\[2pt]{\overline {A'V}}&={\overline {A'V'}}=2{\sqrt {2}}\,.\end{aligned}}}$$

For some particular values of z_A = |z_A'|, half the faces of such a scalenohedron may be isosceles or equilateral.

Example with three different edge lengths:

• The scalenohedron with isotoxal in-out zigzag skew 2×2-gon base vertices U, U', V, V' and right symmetric apices A, A' $${\displaystyle {\begin{alignedat}{5}U&=(3,0,2),&\quad V&=\left(0,{\sqrt {65}},-2\right),&\quad A&=(0,0,7),\\U'&=(-3,0,2),&\quad V'&=\left(0,-{\sqrt {65}},-2\right),&\quad A'&=(0,0,-7),\end{alignedat}}}$$ has congruent scalene upper faces, and congruent equilateral lower faces; thus not all its faces are congruent. Indeed:
  • Upper apical edge lengths:$${\displaystyle {\begin{aligned}{\overline {AU}}&={\overline {AU'}}={\sqrt {34}}\,,\\[2pt]{\overline {AV}}&={\overline {AV'}}={\sqrt {146}}\,;\end{aligned}}}$$
  • Base edge length:$${\displaystyle {\overline {UV}}={\overline {VU'}}={\overline {U'V'}}={\overline {V'U}}=3{\sqrt {10}}\,;}$$
  • Lower apical edge length(s): $${\displaystyle {\begin{aligned}{\overline {A'U}}&={\overline {A'U'}}=3{\sqrt {10}}\,,\\[2pt]{\overline {A'V}}&={\overline {A'V'}}=3{\sqrt {10}}\,.\end{aligned}}}$$

Star bipyramids

A star bipyramid has a star polygon base, and is self-intersecting.^[20]

A regular right symmetric star bipyramid has congruent isosceles triangle faces, and is isohedral.

A p/q-bipyramid has Coxeter diagram .

Example star bipyramids:

Base	5/2-gon	7/2-gon	7/3-gon	8/3-gon
Image

4-polytopes with bipyramidal cells

The dual of the rectification of each convex regular 4-polytopes is a cell-transitive 4-polytope with bipyramidal cells. In the following:

• A is the apex vertex of the bipyramid;
• E is an equator vertex;
• EE is the distance between adjacent vertices on the equator (equal to 1);
• AE is the apex-to-equator edge length;
• AA is the distance between the apices.

The bipyramid 4-polytope will have V_A vertices where the apices of N_A bipyramids meet. It will have V_E vertices where the type E vertices of N_E bipyramids meet.

• ⁠${\displaystyle N_{\overline {AE}}}$⁠ bipyramids meet along each type AE edge.
• ⁠${\displaystyle N_{\overline {EE}}}$⁠ bipyramids meet along each type EE edge.
• ⁠${\displaystyle C_{\overline {AE}}}$⁠ is the cosine of the dihedral angle along an AE edge.
• ⁠${\displaystyle C_{\overline {EE}}}$⁠ is the cosine of the dihedral angle along an EE edge.

As cells must fit around an edge, $${\displaystyle {\begin{aligned}N_{\overline {EE}}\arccos C_{\overline {EE}}&\leq 2\pi ,\\[4pt]N_{\overline {AE}}\arccos C_{\overline {AE}}&\leq 2\pi .\end{aligned}}}$$

4-polytopes with bipyramidal cells

4-polytope properties									Bipyramid properties
Dual of rectified polytope	Coxeter diagram	Cells	VA	VE	NA	NE	⁠${\displaystyle N_{\overline {\!AE}}}$⁠	⁠${\displaystyle N_{\overline {\!EE}}}$⁠	Bipyramid cell	Coxeter diagram	AA	AE[c]	⁠${\displaystyle C_{\overline {AE}}}$⁠	⁠${\displaystyle C_{\overline {EE}}}$⁠
R. 5-cell		10	5	5	4	6	3	3	Triangular		${\textstyle {\frac {2}{3}}}$	0.667	${\textstyle -{\frac {1}{7}}}$	${\textstyle -{\frac {1}{7}}}$
R. tesseract		32	16	8	4	12	3	4	Triangular		${\textstyle {\frac {\sqrt {2}}{3}}}$	0.624	${\textstyle -{\frac {2}{5}}}$	${\textstyle -{\frac {1}{5}}}$
R. 24-cell		96	24	24	8	12	4	3	Triangular		${\textstyle {\frac {2{\sqrt {2}}}{3}}}$	0.745	${\textstyle {\frac {1}{11}}}$	${\textstyle -{\frac {5}{11}}}$
R. 120-cell		1200	600	120	4	30	3	5	Triangular		${\textstyle {\frac {{\sqrt {5}}-1}{3}}}$	0.613	${\textstyle -{\frac {10+9{\sqrt {5}}}{61}}}$	${\textstyle -{\frac {7-12{\sqrt {5}}}{61}}}$
R. 16-cell		24 [d]	8	16	6	6	3	3	Square		${\textstyle {\sqrt {2}}}$	1	${\textstyle -{\frac {1}{3}}}$	${\textstyle -{\frac {1}{3}}}$
R. cubic honeycomb		∞	∞	∞	6	12	3	4	Square		${\textstyle 1}$	0.866	${\textstyle -{\frac {1}{2}}}$	${\textstyle 0}$
R. 600-cell		720	120	600	12	6	3	3	Pentagonal		${\textstyle {\frac {5+3{\sqrt {5}}}{5}}}$	1.447	${\textstyle -{\frac {11+4{\sqrt {5}}}{41}}}$	${\textstyle -{\frac {11+4{\sqrt {5}}}{41}}}$

Other dimensions

A rhombus is a 2-dimensional analog of a right symmetric bipyramid

A generalized n-dimensional "bipyramid" is any n-polytope constructed from an (n − 1)-polytope base lying in a hyperplane, with every base vertex connected by an edge to two apex vertices. If the (n − 1)-polytope is a regular polytope and the apices are equidistant from its center along the line perpendicular to the base hyperplane, it will have identical pyramidal facets.

A 2-dimensional analog of a right symmetric bipyramid is formed by joining two congruent isosceles triangles base-to-base to form a rhombus. More generally, a kite is a 2-dimensional analog of a (possibly asymmetric) right bipyramid, and any quadrilateral is a 2-dimensional analog of a general bipyramid.

See also

• Trapezohedron

Notes

1. The center of a regular polygon is unambiguous, but for irregular polygons sources disagree. Some sources only allow a right pyramid to have a regular polygon as a base. Others define a right pyramid as having its apices on a line perpendicular to the base and passing through its centroid. Polya (1954) restricts right pyramids to those with a tangential polygon for a base, with the apices on a line perpendicular to the base and passing through the incenter.
2. The smallest geometric di-n-gonal bipyramids have eight faces, and are topologically identical to the regular octahedron. In this case (2n = 2×2):
   an isotoxal right (symmetric) didigonal bipyramid is called a rhombic bipyramid,^[13][16] although all its faces are scalene triangles, because its flat polygon base is a rhombus.
3. Given numerically due to more complex form.
4. The rectified 16-cell is the regular 24-cell and vertices are all equivalent – octahedra are regular bipyramids.

Citations

1. Aarts, J. M. (2008). Plane and Solid Geometry. Springer. p. 303. doi:10.1007/978-0-387-78241-6. ISBN 978-0-387-78241-6.
2. Polya, G. (1954). Mathematics and Plausible Reasoning: Induction and analogy in mathematics. Princeton University Press. p. 138. ISBN 0-691-02509-6.
3. Montroll, John (2009). Origami Polyhedra Design. A K Peters. p. 6. ISBN 9781439871065.
4. Trigg, Charles W. (1978). "An infinite class of deltahedra". Mathematics Magazine. 51 (1): 55–57. doi:10.1080/0025570X.1978.11976675. JSTOR 2689647. MR 1572246.
5. Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. p. 62. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
6. Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. ISBN 978-0-521-55432-9.
7. Flusser, Jan; Suk, Tomas; Zitofa, Barbara (2017). 2D and 3D Image Analysis by Moments. John & Sons Wiley. p. 126. ISBN 978-1-119-03935-8.
8. Chang, Ch.; Patzer, A. B. C.; Sülzle, D.; Hauer, H. "Onion-Like Inorganic Fullerenes from a Polyhedral Perspective". In Sattler, Klaus D. (ed.). 21st Century Nanoscience: A Handbook. Taylor & Francis. p. 15-4.
9. McLean, K. Robin (1990). "Dungeons, dragons, and dice". The Mathematical Gazette. 74 (469): 243–256. doi:10.2307/3619822. JSTOR 3619822. S2CID 195047512.
10. Sibley, Thomas Q. (2015). Thinking Geometrically: A Survey of Geometries. Mathematical Association of American. p. 53. ISBN 978-1-939512-08-6.
11. King, Robert B. (1994). "Polyhedral Dynamics". In Bonchev, Danail D.; Mekenyan, O.G. (eds.). Graph Theoretical Approaches to Chemical Reactivity. Springer. doi:10.1007/978-94-011-1202-4. ISBN 978-94-011-1202-4.
12. Armstrong, M. A. (1988). Group and Symmetry. Undergraduate Texts in Mathematics. Springer. p. 39. doi:10.1007/978-1-4757-4034-9. ISBN 978-1-4757-4034-9.
13. "Crystal Form, Zones, Crystal Habit". Tulane.edu. Retrieved 16 September 2017.
14. Spencer 1911, 6. Hexagonal system, rhombohedral division, ditrigonal bipyramidal class, p. 581 (p. 603 on Wikisource).
15. Spencer 1911, 2. Tegragonal system, holosymmetric class, fig. 46, p. 577 (p. 599 on Wikisource).
16. "The 48 Special Crystal Forms". 18 September 2013. Archived from the original on 18 September 2013. Retrieved 18 November 2020.
17. Klein, Cornelis; Philpotts, Anthony R. (2013). Earth Materials: Introduction to Mineralogy and Petrology. Cambridge University Press. p. 108. ISBN 978-0-521-14521-3.
18. Spencer 1911, 6. Hexagonal system, rhombohedral division, holosymmetric class, fig. 68, p. 580 (p. 602 on Wikisource).
19. Spencer 1911, p. 2. Tetragonal system, scalenohedral class, fig. 51, p. 577 (p. 599 on Wikisource).
20. Rankin, John R. (1988). "Classes of polyhedra defined by jet graphics". Computers & Graphics. 12 (2): 239–254. doi:10.1016/0097-8493(88)90036-2.

Works Cited

• Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 4: Duals of the Archimedean polyhedra, prisms and antiprisms
• Spencer, Leonard James (1911). "Crystallography" . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 07 (11th ed.). Cambridge University Press. pp. 569–591.

External links

• Weisstein, Eric W. "Dipyramid". MathWorld.
• Weisstein, Eric W. "Isohedron". MathWorld.
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
  • VRML models (George Hart) <3> <4> <5> <6> <7> <8> <9> <10>
    • Conway Notation for Polyhedra Try: "dPn", where n = 3, 4, 5, 6, ... Example: "dP4" is an octahedron.