Apeirogonal antiprism

In geometry, an apeirogonal antiprism or infinite antiprism^[1] is the arithmetic limit of the family of antiprisms; it can be considered an infinite polyhedron or a tiling of the plane.

Uniform apeirogonal antiprism
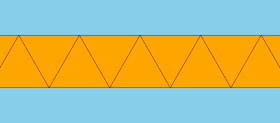Type	Semiregular tiling
Vertex configuration	3.3.3.∞
Schläfli symbol	sr{2,∞} or ${\displaystyle s{\begin{Bmatrix}\infty \\2\end{Bmatrix}}}$
Wythoff symbol	| 2 2 ∞
Coxeter diagram
Symmetry	[∞,2+], (∞22)
Rotation symmetry	[∞,2]+, (∞22)
Bowers acronym	Azap
Dual	Apeirogonal deltohedron
Properties	Vertex-transitive

If the sides are equilateral triangles, it is a uniform tiling. In general, it can have two sets of alternating congruent isosceles triangles, surrounded by two half-planes.

Related tilings and polyhedra

The apeirogonal antiprism is the arithmetic limit of the family of antiprisms sr{2, p} or p.3.3.3, as p tends to infinity, thereby turning the antiprism into a Euclidean tiling.

• 
  The apeirogonal antiprism can be constructed by applying an alternation operation to an apeirogonal prism.
• 
  The dual tiling of an apeirogonal antiprism is an apeirogonal deltohedron.

Similarly to the uniform polyhedra and the uniform tilings, eight uniform tilings may be based from the regular apeirogonal tiling. The rectified and cantellated forms are duplicated, and as two times infinity is also infinity, the truncated and omnitruncated forms are also duplicated, therefore reducing the number of unique forms to four: the apeirogonal tiling, the apeirogonal hosohedron, the apeirogonal prism, and the apeirogonal antiprism.

Order-2 regular or uniform apeirogonal tilings

(∞ 2 2)	Wythoff symbol	Schläfli symbol	Coxeter diagram	Vertex config.	Tiling image	Tiling name
Parent	2 | ∞ 2	{∞,2}		∞.∞		Apeirogonal dihedron
Truncated	2 2 | ∞	t{∞,2}		2.∞.∞
Rectified	2 | ∞ 2	r{∞,2}		2.∞.2.∞
Birectified (dual)	∞ | 2 2	{2,∞}		2∞		Apeirogonal hosohedron
Bitruncated	2 ∞ | 2	t{2,∞}		4.4.∞		Apeirogonal prism
Cantellated	∞ 2 | 2	rr{∞,2}
Omnitruncated (Cantitruncated)	∞ 2 2 |	tr{∞,2}		4.4.∞
Snub	| ∞ 2 2	sr{∞,2}		3.3.3.∞		Apeirogonal antiprism