Loading AI tools
Partition of a sphere's surface into polygons From Wikipedia, the free encyclopedia
In geometry, a spherical polyhedron or spherical tiling is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. A polyhedron whose vertices are equidistant from its center can be conveniently studied by projecting its edges onto the sphere to obtain a corresponding spherical polyhedron.


The most familiar spherical polyhedron is the soccer ball, thought of as a spherical truncated icosahedron. The next most popular spherical polyhedron is the beach ball, thought of as a hosohedron.
Some "improper" polyhedra, such as hosohedra and their duals, dihedra, exist as spherical polyhedra, but their flat-faced analogs are degenerate. The example hexagonal beach ball, {2, 6}, is a hosohedron, and {6, 2} is its dual dihedron.
During the 10th Century, the Islamic scholar Abū al-Wafā' Būzjānī (Abu'l Wafa) studied spherical polyhedra as part of a work on the geometry needed by craftspeople and architects.[1]
The work of Buckminster Fuller on geodesic domes in the mid 20th century triggered a boom in the study of spherical polyhedra.[2] At roughly the same time, Coxeter used them to enumerate all but one of the uniform polyhedra, through the construction of kaleidoscopes (Wythoff construction).[3]
All regular polyhedra, semiregular polyhedra, and their duals can be projected onto the sphere as tilings:
| Schläfli symbol |
{p,q} | t{p,q} | r{p,q} | t{q,p} | {q,p} | rr{p,q} | tr{p,q} | sr{p,q} |
|---|---|---|---|---|---|---|---|---|
| Vertex config. |
pq | q.2p.2p | p.q.p.q | p.2q.2q | qp | q.4.p.4 | 4.2q.2p | 3.3.q.3.p |
| Tetrahedral symmetry (3 3 2) |
 33 |
 3.6.6 |
 3.3.3.3 |
 3.6.6 |
 33 |
 3.4.3.4 |
 4.6.6 |
 3.3.3.3.3 |
 V3.6.6 |
 V3.3.3.3 |
 V3.6.6 |
 V3.4.3.4 |
 V4.6.6 |
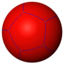 V3.3.3.3.3 | |||
| Octahedral symmetry (4 3 2) |
 43 |
 3.8.8 |
 3.4.3.4 |
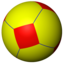 4.6.6 |
 34 |
 3.4.4.4 |
 4.6.8 |
 3.3.3.3.4 |
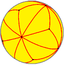 V3.8.8 |
 V3.4.3.4 |
 V4.6.6 |
 V3.4.4.4 |
 V4.6.8 |
 V3.3.3.3.4 | |||
| Icosahedral symmetry (5 3 2) |
 53 |
 3.10.10 |
 3.5.3.5 |
 5.6.6 |
 35 |
 3.4.5.4 |
 4.6.10 |
 3.3.3.3.5 |
 V3.10.10 |
 V3.5.3.5 |
 V5.6.6 |
 V3.4.5.4 |
 V4.6.10 |
 V3.3.3.3.5 | |||
| Dihedral example (p=6) (2 2 6) |
 62 |
 2.12.12 |
 2.6.2.6 |
 6.4.4 |
 26 |
 2.4.6.4 |
 4.4.12 |
 3.3.3.6 |

| n | 2 | 3 | 4 | 5 | 6 | 7 | ... |
|---|---|---|---|---|---|---|---|
| n-Prism (2 2 p) |
 |
 |
 |
 |
 |
 |
... |
| n-Bipyramid (2 2 p) |
 |
 |
 |
 |
 |
 |
... |
| n-Antiprism |  |
 |
 |
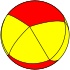 |
 |
 |
... |
| n-Trapezohedron |  |
 |
 |
 |
 |
 |
... |
Spherical tilings allow cases that polyhedra do not, namely hosohedra: figures as {2,n}, and dihedra: figures as {n,2}. Generally, regular hosohedra and regular dihedra are used.
| Space | Spherical | Euclidean | |||||
|---|---|---|---|---|---|---|---|
| Tiling name |
Henagonal hosohedron |
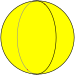
Digonal hosohedron |
Trigonal hosohedron |
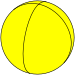
Square hosohedron |
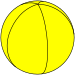
Pentagonal hosohedron |
... | Apeirogonal hosohedron |
| Tiling image |
 |
 |
 |
 |
 |
... | |
| Schläfli symbol |
{2,1} | {2,2} | {2,3} | {2,4} | {2,5} | ... | {2,∞} |
| Coxeter diagram |
... | ||||||
| Faces and edges |
1 | 2 | 3 | 4 | 5 | ... | ∞ |
| Vertices | 2 | 2 | 2 | 2 | 2 | ... | 2 |
| Vertex config. |
2 | 2.2 | 23 | 24 | 25 | ... | 2∞ |
| Space | Spherical | Euclidean | |||||
|---|---|---|---|---|---|---|---|
| Tiling name |
Monogonal dihedron |
Digonal dihedron |
Trigonal dihedron |
Square dihedron |
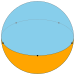
Pentagonal dihedron |
... | Apeirogonal dihedron |
| Tiling image |
 |
 |
 |
 |
 |
... | |
| Schläfli symbol |
{1,2} | {2,2} | {3,2} | {4,2} | {5,2} | ... | {∞,2} |
| Coxeter diagram |
... | ||||||
| Faces | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | ... | 2 {∞} |
| Edges and vertices |
1 | 2 | 3 | 4 | 5 | ... | ∞ |
| Vertex config. |
1.1 | 2.2 | 3.3 | 4.4 | 5.5 | ... | ∞.∞ |
Spherical polyhedra having at least one inversive symmetry are related to projective polyhedra[4] (tessellations of the real projective plane) – just as the sphere has a 2-to-1 covering map of the projective plane, projective polyhedra correspond under 2-fold cover to spherical polyhedra that are symmetric under reflection through the origin.
The best-known examples of projective polyhedra are the regular projective polyhedra, the quotients of the centrally symmetric Platonic solids, as well as two infinite classes of even dihedra and hosohedra:[5]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.