Loading AI tools
There are many relations among the uniform polyhedra.[1][2][3] Some are obtained by truncating the vertices of the regular or quasi-regular polyhedron. Others share the same vertices and edges as other polyhedron. The grouping below exhibit some of these relations.
| Polyhedron | |
| Class | Number and properties |
|---|---|
| Platonic solids |
(5, convex, regular) |
| Archimedean solids |
(13, convex, uniform) |
| Kepler–Poinsot polyhedra |
(4, regular, non-convex) |
| Uniform polyhedra |
(75, uniform) |
| Prismatoid: prisms, antiprisms etc. |
(4 infinite uniform classes) |
| Polyhedra tilings | (11 regular, in the plane) |
| Quasi-regular polyhedra |
(8) |
| Johnson solids | (92, convex, non-uniform) |
| Bipyramids | (infinite) |
| Pyramids | (infinite) |
| Stellations | Stellations |
| Polyhedral compounds | (5 regular) |
| Deltahedra | (Deltahedra, equilateral triangle faces) |
| Snub polyhedra |
(12 uniform, not mirror image) |
| Zonohedron | (Zonohedra, faces have 180°symmetry) |
| Dual polyhedron | |
| Self-dual polyhedron | (infinite) |
| Catalan solid | (13, Archimedean dual) |
The relations can be made apparent by examining the vertex figures obtained by listing the faces adjacent to each vertex (remember that for uniform polyhedra all vertices are the same, that is vertex-transitive). For example, the cube has vertex figure 4.4.4, which is to say, three adjacent square faces. The possible faces are
- 3 - equilateral triangle
- 4 - square
- 5 - regular pentagon
- 6 - regular hexagon
- 8 - regular octagon
- 10 - regular decagon
- 5/2 - pentagram
- 8/3 - octagram
- 10/3 - decagram
Some faces will appear with reverse orientation which is written here as
- -3 - a triangle with reverse orientation (often written as 3/2)
Others pass through the origin which we write as
- 6* - hexagon passing through the origin
The Wythoff symbol relates the polyhedron to spherical triangles. Wythoff symbols are written p|q r, p q|r, p q r| where the spherical triangle has angles π/p,π/q,π/r, the bar indicates the position of the vertices in relation to the triangle.

Johnson (2000) classified uniform polyhedra according to the following:
- Regular (regular polygonal vertex figures): pq, Wythoff symbol q|p 2
- Quasi-regular (rectangular or ditrigonal vertex figures): p.q.p.q 2|p q, or p.q.p.q.p.q, Wythoff symbol 3|p q
- Versi-regular (orthodiagonal vertex figures), p.q*.-p.q*, Wythoff symbol q q|p
- Truncated regular (isosceles triangular vertex figures): p.p.q, Wythoff symbol q 2|p
- Versi-quasi-regular (dipteroidal vertex figures), p.q.p.r Wythoff symbol q r|p
- Quasi-quasi-regular (trapezoidal vertex figures): p*.q.p*.-r q.r|p or p.q*.-p.q* p q r|
- Truncated quasi-regular (scalene triangular vertex figures), p.q.r Wythoff symbol p q r|
- Snub quasi-regular (pentagonal, hexagonal, or octagonal vertex figures), Wythoff symbol p q r|
- Prisms (truncated hosohedra),
- Antiprisms and crossed antiprisms (snub dihedra)
The format of each figure follows the same basic pattern
- image of polyhedron
- name of polyhedron
- alternate names (in brackets)
- Wythoff symbol
- Numbering systems: W - number used by Wenninger in polyhedra models, U - uniform indexing, K - Kaleido indexing, C - numbering used in Coxeter et al. 'Uniform Polyhedra'.
- Number of vertices V, edges E, Faces F and number of faces by type.
- Euler characteristic χ = V - E + F
The vertex figures are on the left, followed by the Point groups in three dimensions#The seven remaining point groups, either tetrahedral Td, octahedral Oh or icosahedral Ih.
Regular polyhedra and their truncated forms
Column A lists all the regular polyhedra, column B list their truncated forms. Regular polyhedra all have vertex figures pr: p.p.p etc. and Wythoff symbol p|q r. The truncated forms have vertex figure q.q.r (where q=2p and r) and Wythoff p q|r.
| vertex figure | group | A: regular: p.p.p | B: truncated regular: p.p.r |
| Td |
|
| |
 3.3.3.3 |
Oh |
|
|
 4.4.4 |
Oh |
|
|
| Ih |
|
| |
 5.5.5 |
Ih |
|
|
| Ih |
|
| |
 3.3.3.3.3 |
Ih |
|
|
| Ih |
|
||
| Ih |
|
In addition there are three quasi-truncated forms. These also class as truncated-regular polyhedra.
| vertex figures | Group Oh | Group Ih | Group Ih |
|
|
|
|
Truncated forms of quasi-regular polyhedra
Column A lists some quasi-regular polyhedra, column B lists normal truncated forms, column C shows quasi-truncated forms, column D shows a different method of truncation. These truncated forms all have a vertex figure p.q.r and a Wythoff symbol p q r|.
| vertex figure | group | A: quasi-regular: p.q.p.q | B: truncated quasi-regular: p.q.r | C: truncated quasi-regular: p.q.r | D: truncated quasi-regular: p.q.r |
 3.4.3.4 |
Oh |
|
|
|
|
 3.5.3.5 |
Ih |
|
|
|
|
|
Ih |
|
|
|||
 3.5/2.3.5/2 |
Ih |
|
Regular
These are all mentioned elsewhere, but this table shows some relations. They are all regular apart from the tetrahemihexahedron which is versi-regular.
| vertex figure | V | E | group | regular | regular/versi-regular |
 3.3.3.3 3.4*.-3.4* |
6 | 12 | Oh |
|
|
| 12 | 30 | Ih |
|
| |
| 12 | 30 | Ih |
|
|
Quasi-regular and versi-regular
Rectangular vertex figures, or crossed rectangles first column are quasi-regular second and third columns are hemihedra with faces passing through the origin, called versi-regular by some authors.
| vertex figure | V | E | group | quasi-regular: p.q.p.q | versi-regular: p.s*.-p.s* | versi-regular: q.s*.-q.s* |
 3.4.3.4 |
12 | 24 | Oh |
|
|
|
 3.5.3.5 |
30 | 60 | Ih |
|
|
|

3.5/2.3.5/2 |
30 | 60 | Ih |
|
|
|
 5.5/2.5.5/2 |
30 | 60 | Ih |
|
|
|
Ditrigonal regular and versi-regular
Ditrigonal (that is di(2) -tri(3)-ogonal) vertex figures are the 3-fold analog of a rectangle. These are all quasi-regular as all edges are isomorphic. The compound of 5-cubes shares the same set of edges and vertices. The cross forms have a non-orientable vertex figure so the "-" notation has not been used and the "*" faces pass near rather than through the origin.
| vertex figure | V | E | group | ditrigonal | crossed-ditrigonal | crossed-ditrigonal |

5/2.3.5/2.3.5/2.3 |
20 | 60 | Ih |
|
|
|
versi-quasi-regular and quasi-quasi-regular
Group III: trapezoid or crossed trapezoid vertex figures. The first column include the convex rhombic polyhedra, created by inserting two squares into the vertex figures of the Cuboctahedron and Icosidodecahedron.
| vertex figure | V | E | group | trapezoid: p.q.r.q | crossed-trapezoid: p.s*.-r.s* | crossed-trapezoid: q.s*.-q.s* |
 3.4.4.4 |
24 | 48 | Oh |
|
|
|
 3.8/3.4.8/3 |
24 | 48 | Oh |
|
|
|
 3.4.5.4 |
60 | 120 | Ih |
|
|
|

5/2.4.5.4 |
60 | 120 | Ih |
|
|
|
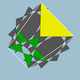 3.10/3.5/2.10/3 |
60 | 120 | Ih |
|
|
|
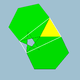
3.6.5/2.6 |
60 | 120 | Ih |
|
|
|
 3.10/3.5.10/3 |
60 | 120 | Ih |
|
|
|
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.