Winkel

Dieser Artikel erläutert den Begriff ebener Winkel in der Geometrie; für weitere Bedeutungen siehe Winkel (Begriffsklärung).

Ein Winkel ist in der Geometrie ein Teil der Ebene, der von zwei in der Ebene liegenden Strahlen (Halbgeraden) mit gemeinsamem Anfangspunkt begrenzt wird.

Winkel

Der gemeinsame Anfangspunkt der beiden Strahlen wird Scheitelpunkt des Winkels, Winkelscheitel oder kurz Scheitel genannt; die Strahlen heißen Schenkel des Winkels oder Winkelschenkel. Ein Winkel kann durch drei Punkte festgelegt werden, von denen einer den Scheitel des Winkels bildet und die beiden anderen auf je einem Schenkel des Winkels liegen.

Die physikalische Größe, die die relative Lage der Strahlen zueinander beschreibt, wird als Winkelweite oder Winkelabstand (Winkeldistanz) bezeichnet, üblicherweise auch verkürzend als Winkel, wenn eine Unterscheidung von dem geometrischen Objekt nicht notwendig ist, beispielsweise in der Physik. Die Größe des Winkels wird mit einem Winkelmaß angegeben.

Die Winkelweite kann auch als Maß einer ebenen Drehung definiert werden.

Zur Unterscheidung vom Raumwinkel wird der hier definierte Winkel auch als ebener Winkel bezeichnet.

Definition

In der Geometrie sind zur Definition des Winkels als Objekt verschiedene Ansätze möglich. Dabei lassen sich zwei Typen unterscheiden:

• Der ungerichtete Winkel, der durch eine vorzeichenlose Winkelweite gekennzeichnet ist.
• Der gerichtete Winkel, der über eine Orientierung verfügt, und als Drehwinkel oder Winkelabstand gemessen wird.

Darstellung als Strahlenpaar

Die eingangs angeführte Definition zweier von einem Punkt ausgehenden Strahlen ist in die Anwendungen wie etwa die Koordinatensysteme und deren Achsen eingebunden.

Darstellung als Halbgeradenpaar

Darstellung als Halbgeradenpaar

Der Winkel ist ein geometrisches Gebilde bestehend aus zwei Halbgeraden mit demselben Ursprung.

Sind ${\displaystyle f}$, ${\displaystyle g}$ zwei Geraden, die sich in einem Punkt ${\displaystyle S}$ schneiden, so teilt der Punkt ${\displaystyle S}$ die Geraden ${\displaystyle f}$, ${\displaystyle g}$ in Halbgeraden. Je eine Halbgerade von ${\displaystyle f}$ und ${\displaystyle g}$ (die Schenkel) zusammen mit ${\displaystyle S}$ (dem Scheitel) bilden einen Winkel.

Über die „ursprünglichen“ Geraden ermöglicht diese Darstellung etwa Betrachtungen über die verschiedenen Winkelpaare.

Darstellung als Teil der Ebene

Darstellung als Teil der Ebene

Der Winkel (besser: das Winkelfeld) ist ein Teilbereich der Zeichenebene, der von zwei Halbstrahlen oder Halbgeraden begrenzt wird. Diese bilden den Rand, und der Rest des Winkelfeldes das Innere. Diese Definition wird im Schulunterricht verwendet und betont das „Körperhafte“ des Gebildes und dient – über die Festlegung eines Innen- und Außenraums – der Einführung in die Dreiecksgeometrie: Das Dreieck lässt sich als Schnittmenge zweier Winkel mit einem gemeinsamen Schenkel definieren.

Ad hoc ist bei diesen drei Ansätzen der Winkel ein ungerichteter Winkel, erst eine zusätzliche Auszeichnung einer der beiden Halbstrahlen oder Halbgeraden als die „erste“ ermöglicht die Angabe eines gerichteten Winkels.

Darstellung als Drehung

Drehwinkel

Man kann auch sagen, dass ein Winkel durch eine Drehung eines Strahls oder einer Halbgeraden in einer Ebene um seinen bzw. ihren Anfangspunkt entsteht.

Da der Strahl auf zwei verschiedene Möglichkeiten gedreht werden kann, muss zusätzlich die Drehrichtung angegeben werden:

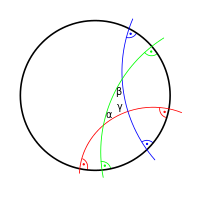
• Linksdrehung: gegen den Uhrzeigersinn, auch mathematisch positiver Drehsinn genannt (Winkel ist positiv) – im Bild grün dargestellt.
• Rechtsdrehung: mit dem Uhrzeigersinn, auch mathematisch negativer Drehsinn genannt (Winkel ist negativ) – im Bild violett dargestellt.

In der Mathematik ist es üblich, die Drehung gegen den Uhrzeigersinn – also im mathematisch positiven Drehsinn – auszuführen. Wenn die Drehung andersherum erfolgen soll, sollte dies ausdrücklich angegeben werden.

In der Geodäsie (Vermessungswesen) wird der Winkel im Uhrzeigersinn, also rechtsdrehend von 0 gon bis 400 gon gezählt. Da in der Geodäsie per Definition keine negativen Winkel existieren, ist der Drehsinn positiv. Analog zur Uhr, auch hier wird von 0 bis 24 h positiv, rechtsdrehend gezählt. Alle geodätischen Messinstrumente werden zur Richtungs- oder Winkelmessung rechtsherum gedreht.

Bezeichnung von Winkeln

Die Angabe eines Winkels erfolgt nach DIN 1302 oder ISO 80000-2.

• Winkel werden meistens mit kleinen griechischen Buchstaben, z. B. ${\displaystyle \alpha }$ oder ${\displaystyle \beta }$, bezeichnet.
• Ein Winkel ${\displaystyle \angle fg}$ ist ein Winkel zwischen zwei Halbstrahlen, Geraden, Kanten und ähnlichem. Er wird dann von ${\displaystyle f}$ ausgehend Richtung ${\displaystyle g}$ gezählt.
• Alternativ kann man die drei Punkte angeben, die den Winkel definieren, wobei der Scheitelpunkt immer in der Mitte steht, z. B. Winkel ABC, ${\displaystyle \angle ABC}$ oder veraltet ${\displaystyle {\widehat {ABC}}}$. Dies bezeichnet den Winkel zwischen ${\displaystyle [BA]}$ und ${\displaystyle [BC]}$, wobei ${\displaystyle [BA]}$ im mathematisch positiven Drehsinn auf ${\displaystyle [BC]}$ gedreht wird.
• Im englischen Sprachraum ist auch nur die Angabe des Scheitels ${\displaystyle \angle B}$ bzw. ${\displaystyle {\hat {B}}}$ üblich.

Für den Formelsatz steht das Zeichen »∠« (HTML ∠/∠, TeX \angle, Unicode U+2220) zur Verfügung, für den gerichteten Winkel auch »∡« (TeX \measuredangle, U+2221 measured angle, keine HTML-Entität), die sich beide im Unicode-Block Mathematische Operatoren finden. Das liegende Winkelzeichen entspricht den angloamerikanischen Gewohnheiten, im europäischen Formelsatz ist ein Zeichen üblich, das dem amerikanischen »∢« U+2222 für den Raumwinkel zum Verwechseln ähnlich sieht. »∠« findet auch für Neigung und Winkligkeit (Lagetoleranz, DIN EN ISO 1101) Verwendung. Speziell für den rechten Winkel verwendet man alternativ einen Winkel ohne Zusatz »∟«, einen Winkel mit Bogen und Punkt »⦝« oder einen Winkel mit Bogen »⊾«, in der Technik auch einen Winkel mit Quadrat »⦜« oder das Zeichen für Orthogonalität ${\displaystyle \perp }$.

∠

ungerichteter Winkel
bzw. Winkel allgemein

∡

gerichteter Winkel

∢

Raumwinkel

∟ ⦝ ⊾ ⦜${\displaystyle \perp }$

alternative Kennzeichnung des rechten Winkels

Winkelmaße und Maßeinheiten für Winkel

Ausführliche Informationen bietet der Hauptartikel Winkelmaß, Umrechnungen sind bei den einzelnen Maßen zu finden.

Winkelmaß	Maßeinheit	1 Vollwinkel =	Einheitenzeichen
—	Vollwinkel	1
Bogenmaß	Radiant	2π	rad
Gradmaß	Grad (Bogenminute, Bogensekunde)	360	° (′, ″)
Geodätisches Winkelmaß	Gon (veraltet: Neugrad)	400	gon (veraltet: g)
Zeitmaß	Stunden, Minuten, Sekunden	24	h, m, s
—	Nautischer Strich	32	¯
—	Artilleristischer Strich (Schweiz: Artilleriepromille)	6400	mil (A‰)
—	Prozent, Promille	nichtlinear	%, ‰

Weitere Formen der Angabe eines Winkels:

• Der Tangens der Winkelweite des Steigungswinkels (auch Steigungsmaß genannt, entspricht der Maßangabe in Prozent)
• Ein Paar ${\displaystyle (x;y)}$ mit Cosinus und Sinus (entspricht den kartesischen Koordinaten des Punktes auf dem Einheitskreis)

Arten von Winkeln

Winkel nach Größe

	[°]	[rad] (mit ${\displaystyle \pi }$)	[rad] (mit ${\displaystyle \tau }$)	[${\displaystyle \mathrm {gon} }$]
Nullwinkel	${\displaystyle \alpha =0^{\circ }}$	${\displaystyle \alpha =0}$	${\displaystyle \alpha =0}$	${\displaystyle \alpha =0\,\mathrm {gon} }$
spitzer Winkel < ${\displaystyle {\tfrac {1}{4}}}$ Vollwinkel	${\displaystyle \alpha <90^{\circ }}$	${\displaystyle \alpha <{\frac {\pi }{2}}}$	${\displaystyle \alpha <{\frac {\tau }{4}}}$	${\displaystyle \alpha <100\,\mathrm {gon} }$
rechter Winkel = ${\displaystyle {\tfrac {1}{4}}}$ Vollwinkel	${\displaystyle \alpha =90^{\circ }}$	${\displaystyle \alpha ={\frac {\pi }{2}}}$	${\displaystyle \alpha ={\frac {\tau }{4}}}$	${\displaystyle \alpha =100\,\mathrm {gon} }$
stumpfer Winkel > ${\displaystyle {\tfrac {1}{4}}}$ Vollwinkel und < ${\displaystyle {\tfrac {1}{2}}}$ Vollwinkel	${\displaystyle 90^{\circ }<\alpha <180^{\circ }}$	${\displaystyle {\frac {\pi }{2}}<\alpha <\pi }$	${\displaystyle {\frac {\tau }{4}}<\alpha <{\frac {\tau }{2}}}$	${\displaystyle 100\,\mathrm {gon} <\alpha <200\,\mathrm {gon} }$
gestreckter Winkel = ${\displaystyle {\tfrac {1}{2}}}$ Vollwinkel	${\displaystyle \alpha =180^{\circ }}$	${\displaystyle \alpha =\pi }$	${\displaystyle \alpha ={\frac {\tau }{2}}}$	${\displaystyle \alpha =200\,\mathrm {gon} }$
überstumpfer (erhabener) Winkel > ${\displaystyle {\tfrac {1}{2}}}$ Vollwinkel und < 1 Vollwinkel	${\displaystyle 180^{\circ }<\alpha <360^{\circ }}$	${\displaystyle \pi <\alpha <2\pi }$	${\displaystyle {\frac {\tau }{2}}<\alpha <\tau }$	${\displaystyle 200\,\mathrm {gon} <\alpha <400\,\mathrm {gon} }$
voller Winkel, Vollwinkel (Vollkreis)	${\displaystyle \alpha =360^{\circ }}$	${\displaystyle \alpha =2\pi }$	${\displaystyle \alpha =\tau }$	${\displaystyle \alpha =400\,\mathrm {gon} }$

Der Vollwinkel ist in Deutschland, Österreich und der Schweiz eine gesetzliche Einheit im Messwesen, er besitzt kein Einheitenzeichen.

Schnittwinkel

Zwischen zwei sich schneidenden Geraden existieren vier Winkel. Jeweils zwei nebeneinander liegende summieren sich dabei zu 180°. Der rechte Winkel hat die Besonderheit, dass diese beiden Winkel genau gleich sind. Jeweils zwei gegenüberliegende Winkel sind gleich. Der Vollwinkel hat die Besonderheit, dass zwei der Winkel null sind.

Zwei Geraden oder Strecken, die sich im rechten Winkel schneiden, nennt man zueinander orthogonal. In einer Zeichnung wird der rechte Winkel durch einen Viertelkreis mit Punkt oder durch ein Quadrat dargestellt.

Spezielle Winkelpaare

Komplement- oder Komplementärwinkel

Die Geometrie kennt besondere Bezeichnungen für Paare von Winkeln, die zueinander in einer besonderen Beziehung stehen. Die für solche Winkel geltenden Gesetze helfen bei der Untersuchung komplexerer geometrischer Objekte.

Komplementwinkel oder Komplementärwinkel

Zwei Winkel heißen Komplementwinkel oder Komplementärwinkel, wenn sie sich zu einem rechten Winkel (90°) ergänzen.

Supplementwinkel oder Ergänzungswinkel

Supplement- oder Ergänzungswinkel

Nebenwinkel

Zwei Winkel heißen Supplementwinkel (auch: Supplementärwinkel), Supplement, Ergänzungswinkel oder kurz E-Winkel, wenn sie sich zu 180° ergänzen.

Nebenwinkel

Schneiden sich zwei Geraden, so bezeichnet man ein Paar benachbarter Winkel als Nebenwinkel.

Nebenwinkel ergänzen sich zu 180°.

Sie sind also Supplementwinkel.

Scheitelwinkel oder Gegenwinkel

Scheitelwinkel

Schneiden sich zwei Geraden, so bezeichnet man das Paar gegenüberliegender Winkel als Scheitelwinkel oder Gegenwinkel.

Scheitelwinkel sind immer gleich groß.

Die Bezeichnung Scheitelwinkel kommt daher, dass die beiden Winkel durch Punktspiegelung am Scheitelpunkt aufeinander abgebildet werden.

Stufenwinkel oder F-Winkel

→ Hauptartikel: Stufenwinkelsatz

Stufen- oder F-Winkel

Schneidet eine Gerade ${\displaystyle g}$ zwei Geraden ${\displaystyle h}$ und ${\displaystyle h'}$, so heißen die Winkel, die auf derselben Seite von ${\displaystyle g}$ und auf einander entsprechenden Seiten von ${\displaystyle h}$ bzw. ${\displaystyle h'}$ liegen, Stufen- oder F-Winkel.^[1] Für den Fall, dass die Geraden ${\displaystyle h}$ und ${\displaystyle h'}$ parallel sind, gilt:

Stufenwinkel an Parallelen sind gleich groß.

Aus der Winkelgleichheit kann umgekehrt auf die Parallelität von Geraden geschlossen werden: Wird ein Geradenpaar ${\displaystyle h}$, ${\displaystyle h'}$ von einer weiteren Geraden ${\displaystyle g}$ so geschnitten, dass die Schnittwinkel auf derselben Seite von ${\displaystyle g}$ und auf einander entsprechenden Seiten von ${\displaystyle h}$ und ${\displaystyle h'}$ gleich groß sind, so sind die Geraden ${\displaystyle h}$ und ${\displaystyle h'}$ parallel.

Wechselwinkel oder Z-Winkel

Wechsel- oder Z-Winkel

Schneidet eine Gerade ${\displaystyle g}$ zwei Geraden ${\displaystyle h}$ und ${\displaystyle h'}$, so heißen die Winkel, die auf unterschiedlichen Seiten von ${\displaystyle g}$ und entgegengesetzten Seiten von ${\displaystyle h}$ bzw. ${\displaystyle h'}$ liegen, Wechsel- oder Z-Winkel.^[1] Für den Fall, dass die Geraden ${\displaystyle h}$ und ${\displaystyle h'}$ parallel sind, gilt:

Wechselwinkel an Parallelen sind gleich groß.

Aus der Winkelgleichheit kann umgekehrt auf die Parallelität von Geraden geschlossen werden: Wird ein Geradenpaar ${\displaystyle h}$, ${\displaystyle h'}$ von einer weiteren Geraden ${\displaystyle g}$ so geschnitten, dass die Schnittwinkel auf unterschiedlichen Seiten von ${\displaystyle g}$ und unterschiedlichen Seiten von ${\displaystyle h}$ bzw. ${\displaystyle h'}$ gleich groß sind, so sind die Geraden ${\displaystyle h}$ und ${\displaystyle h'}$ parallel.

Nachbarwinkel oder E-Winkel

Nachbar- oder E-Winkel

Schneidet eine Gerade ${\displaystyle g}$ zwei weitere parallele Geraden ${\displaystyle h}$ und ${\displaystyle h'}$, so bezeichnet man die Winkel, die auf derselben Seite von ${\displaystyle g}$, aber auf unterschiedlichen Seiten von ${\displaystyle h}$ und ${\displaystyle h'}$ liegen, als Nachbar- oder E-Winkel.^[1]

Nachbarwinkel ergänzen sich zu 180°.

Aus der Ergänzung der Winkel zu 180° kann umgekehrt auf die Parallelität von Geraden geschlossen werden: Wird ein Geradenpaar ${\displaystyle h}$, ${\displaystyle h'}$ von einer weiteren Geraden ${\displaystyle g}$ so geschnitten, dass sich die Schnittwinkel, die auf derselben Seite von ${\displaystyle g}$, aber jeweils auf unterschiedlichen Seiten von ${\displaystyle h}$ und ${\displaystyle h'}$ liegen, zu 180° ergänzen, so sind die Geraden ${\displaystyle h}$ und ${\displaystyle h'}$ parallel.

Die Eigenschaft, dass sich Nachbarwinkel zu 180° ergänzen, folgt direkt aus dem Parallelenaxiom der euklidischen Geometrie. Die oben genannten Eigenschaften von Stufen- und Wechselwinkeln lassen sich aus der Betrachtung von Neben- und Scheitelwinkeln von Nachbarwinkeln herleiten.

Normalwinkel

Normalwinkel a)

Normalwinkel b)

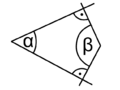Winkel, deren Schenkel paarweise aufeinander normal stehen werden Normalwinkel genannt. Sie sind gleich groß oder ergänzen sich zu 180°.^[2] Vergleiche nebenstehende Abbildungen.

Winkel nach Dimensionen

Zweidimensionale Winkel

Der einfachste Fall für Winkel sind die in diesem Artikel ausführlich beschriebenen Winkel in der zweidimensionalen euklidischen Ebene. Sie sind meistens die intuitive und umgangssprachliche Vorstellung, wenn von Winkeln die Rede ist.

Dreidimensionale Winkel

Im dreidimensionalen euklidischen Raum existieren ebenfalls Winkel, die der klassischen Vorstellung von Winkeln entsprechen. Das können zum Beispiel die Innenwinkel der Seitenflächen (Polygone) von Polyedern sein.

→ Hauptartikel: Diederwinkel

Diederwinkel zwischen zwei Flächen. Die Strecken, die den Winkel einschließen, entstehen, wenn diese Flächen orthogonal von einer Ebene geschnitten werden.

Dazu kommen die Neigungswinkel zwischen zwei Flächen oder Halbebenen, die Diederwinkel, Flächenwinkel oder Torsionswinkel. Diese Begriffe hängen vom fachlichen Kontext ab. Diederwinkel werden von zwei Flächen begrenzt, die jeweils von drei Punkten aufgespannt werden. Wenn diese Flächen orthogonal von einer Ebene geschnitten werden, entstehen zwei Strecken, die einen Winkel im herkömmlichen Sinn einschließen. Auch der Winkel zwischen zwei nicht parallelen Ebenen kann als Diederwinkel verstanden werden. Wenn diese zwei Ebenen orthogonal von einer dritten Ebene geschnitten werden, entstehen zwei Geraden, die zwei Scheitelwinkel im herkömmlichen Sinn einschließen. Diederwinkel werden ebenfalls in Gradmaß oder Bogenmaß angegeben und können maximal 360° oder ${\displaystyle 2\cdot \pi }$ betragen.

→ Hauptartikel: Raumwinkel

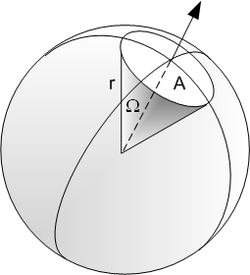
Der Raumwinkel ist das dreidimensionale Gegenstück zum zweidimensionalen für die Ebene definierten Winkel. Er beschreibt den Anteil am gesamten dreidimensionalen Raum, der z. B. im Inneren eines gegebenen Kegel- oder Pyramidenmantels liegt.

Der Raumwinkel wird zur Verdeutlichung meist in der Einheit Steradiant (sr) angegeben. Dies entspricht dem Bogenmaß mit der Einheit Radiant (rad) beim ebenen Winkel. Ein Raumwinkel von 1 sr umschließt auf einer Kugel mit dem Radius 1 m eine Fläche von 1 m². Da der Flächeninhalt einer ganzen Kugeloberfläche ${\displaystyle A=4\pi r^{2}}$ ist, ist der zugehörige volle Raumwinkel

${\displaystyle \Omega =4\cdot \pi \ \mathrm {sr} \approx 12{,}56637\ \mathrm {sr} }$.

• 
  Kanonischer Raumwinkel
• 
  Raumwinkel einer Pyramide
• 
  Raumwinkel eines Tetraeders

Winkel nach Geometrien

Üblicherweise werden Winkel im euklidischen Raum betrachtet. Diese Art von Geometrie wird euklidische Geometrie genannt.

Es können jedoch auch Winkel auf der Kugeloberfläche betrachtet und berechnet werden. Dann gelten andere Sätze und Gleichungen für die Winkel und Längen. Für die Berechnung der Winkel eines Kugeldreiecks ist zum Beispiel der Sinussatz für Kugeldreiecke und der Kosinussatz für Kugeldreiecke wichtig. Weitere Sätze sind unter Sphärische Trigonometrie – Kugeldreieck zu finden.

In einem hyperbolischer Raum gelten ebenfalls andere Sätze und Gleichungen für die betrachteten Winkel und Längen. Diese Art von Geometrie wird hyperbolische Geometrie genannt.

• 
  Kugeldreieck mit Winkeln
• 
  Dreieck mit Winkeln im hyperbolischen Raum

Berechnung von Winkeln

Winkel im Dreieck

Rechtwinkliges Dreieck

Ein rechtwinkliges Dreieck hat zwei spitze Winkel ${\displaystyle \alpha }$ und ${\displaystyle \beta }$.

Wenn im rechtwinkligen Dreieck einer der spitzen Winkel ${\displaystyle \alpha }$ und ${\displaystyle \beta }$ gegeben ist, ist der andere eindeutig bestimmt, denn es gilt ${\displaystyle \alpha +\beta =90^{\circ }}$.

Sind zwei der drei Seitenlängen ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle c}$ bekannt, dann können die Winkel ${\displaystyle \alpha }$ und ${\displaystyle \beta }$ mithilfe einer inversen Winkelfunktion (Arkusfunktion) berechnet werden. Es gilt

${\displaystyle \alpha =\arcsin \left({\frac {a}{c}}\right)=\arccos \left({\frac {b}{c}}\right)=\arctan \left({\frac {a}{b}}\right)=\operatorname {arccot} \left({\frac {b}{a}}\right)=\operatorname {arcsec} \left({\frac {c}{b}}\right)=\operatorname {arccsc} \left({\frac {c}{a}}\right)}$,

${\displaystyle \beta =\arcsin \left({\frac {b}{c}}\right)=\arccos \left({\frac {a}{c}}\right)=\arctan \left({\frac {b}{a}}\right)=\operatorname {arccot} \left({\frac {a}{b}}\right)=\operatorname {arcsec} \left({\frac {c}{a}}\right)=\operatorname {arccsc} \left({\frac {c}{b}}\right)}$.

Allgemeines Dreieck

Ein Dreieck mit den Innenwinkeln ${\displaystyle \alpha }$, ${\displaystyle \beta }$ und ${\displaystyle \gamma }$

Wenn im allgemeinen Dreieck zwei der drei Innenwinkel ${\displaystyle \alpha }$, ${\displaystyle \beta }$ und ${\displaystyle \gamma }$ gegeben sind, ist der dritte eindeutig bestimmt, denn es gilt ${\displaystyle \alpha +\beta +\gamma =180^{\circ }}$.

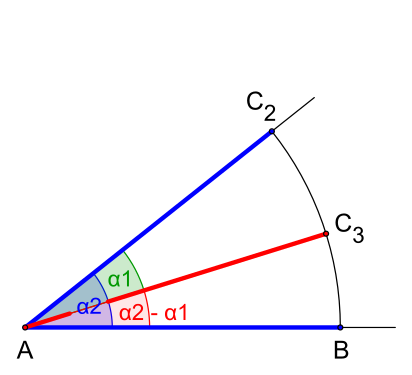
Sind zwei Seitenlängen und ein gegenüberliegender Winkel gegeben, dann kann der andere gegenüberliegende Winkel mithilfe des Sinussatz berechnet werden. Es gilt zum Beispiel ${\displaystyle \sin(\alpha )={\frac {a\cdot \sin \beta }{b}}}$. Anwenden der Umkehrfunktion des Sinus (Arkussinus) auf beiden Seiten der Gleichung ergibt ${\displaystyle \alpha =\arcsin \left({\frac {a\cdot \sin \beta }{b}}\right)}$.

Sind alle drei Seitenlängen gegeben, dann können die Winkel mithilfe des Kosinussatz berechnet werden. Es gilt zum Beispiel ${\displaystyle \cos \alpha ={\frac {b^{2}+c^{2}-a^{2}}{2\cdot b\cdot c}}}$. Anwenden der Umkehrfunktion des Kosinus (Arkuskosinus) auf beiden Seiten der Gleichung ergibt ${\displaystyle \alpha =\arccos {\frac {b^{2}+c^{2}-a^{2}}{2\cdot b\cdot c}}}$.

Sind die Koordinaten der drei Ecken ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ eines Dreiecks gegeben, dann können die Innenwinkel als Winkel zwischen zwei Vektoren berechnet werden. Sind ${\displaystyle {\vec {b}}={\overrightarrow {AB}}}$ und ${\displaystyle {\vec {c}}={\overrightarrow {AC}}}$ die von ${\displaystyle A}$ ausgehenden Vektoren, dann ergibt sich der Innenwinkel ${\displaystyle \alpha =\arccos {\frac {{\vec {b}}\cdot {\vec {c}}}{|{\vec {b}}||{\vec {c}}|}}}$. Dabei ist ${\displaystyle {\vec {b}}\cdot {\vec {c}}}$ das Skalarprodukt und ${\displaystyle |{\vec {b}}||{\vec {c}}|}$ das Produkt der Längen der Vektoren.

Kugeldreieck

→ Hauptartikel: Kugeldreieck

Zur Berechnung der Winkel im Kugeldreieck kann entsprechend der Sinussatz für Kugeldreiecke und der Kosinussatz für Kugeldreiecke verwendet werden, indem die Gleichung durch Anwenden von Arkussinus oder Arkuskosinus nach dem gesuchten Winkel aufgelöst wird.

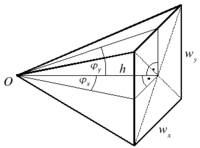
Winkel im Tetraeder

Ein regelmäßiges Tetraeder mit dem Innenwinkel ${\displaystyle \alpha =60^{\circ }}$, dem Tetraederwinkel ${\displaystyle \tau =\arccos \left(-{\frac {1}{3}}\right)\approx 109^{\circ }\;28^{\prime }\;16^{\prime \prime }}$, dem Diederwinkel ${\displaystyle \beta =\arccos \left({\frac {1}{3}}\right)\approx 70^{\circ }\;31^{\prime }\;44^{\prime \prime }}$ und dem Winkel ${\displaystyle \gamma =\arctan \left({\sqrt {2}}\right)\approx 54^{\circ }\;44^{\prime }\;8^{\prime \prime }}$ zwischen Kante und Fläche

Siehe auch: Tetraeder – Berechnung des regelmäßigen Tetraeders

Siehe auch: Tetraeder – Berechnung eines beliebigen Tetraeders

Im allgemeinen Tetraeder kommen zweidimensionale Winkel vor, zum Beispiel als Innenwinkel der dreieckigen Seitenflächen. Außerdem hat ein Tetraeder Diederwinkel zwischen benachbarten Seitenflächen und Raumwinkel in den Ecken. Das regelmäßige Tetraeder und seine Winkel sind ein Spezialfall des allgemeinen Tetraeders.

Neigungswinkel einer Geraden

Ist eine Gerade in der Ebene mit ${\displaystyle ax+by=c}$ in Koordinatenform gegeben, dann gilt für den Neigungswinkel ${\displaystyle \alpha }$ dieser Geraden:

${\displaystyle \tan \alpha ={\frac {a}{b}}}$.

Das folgt aus der Definition des Tangens. Anwenden der Umkehrfunktion des Tangens (Arkustangens) auf beiden Seiten der Gleichung ergibt

${\displaystyle \alpha =\arctan {\frac {a}{b}}}$.

Für den Spezialfall ${\displaystyle b=0}$ verläuft die Gerade senkrecht und diese Gleichungen sind nicht definiert. Die Funktion ${\displaystyle \tan \alpha }$ (Tangens) hat Polstellen bei ${\displaystyle \alpha =90^{\circ }}$ und ${\displaystyle \alpha =-90^{\circ }}$.^[3]

Schnittwinkel zwischen zwei Geraden

Sind die zwei sich schneidenden Geraden ${\displaystyle g_{1}=\{\mathbf {p_{1}} +\lambda \mathbf {r_{1}} \mid \lambda \in \mathbb {R} \}}$ und ${\displaystyle g_{2}=\{\mathbf {p_{2}} +\lambda \mathbf {r_{2}} \mid \lambda \in \mathbb {R} \}}$ mit den Ortsvektoren ${\displaystyle \mathbf {p_{1}} }$ und ${\displaystyle \mathbf {p_{2}} }$ und den linear unabhängigen Richtungsvektoren ${\displaystyle \mathbf {r_{1}} }$ und ${\displaystyle \mathbf {r_{2}} }$ gegeben, dann ist der Schnittwinkel ${\displaystyle \theta }$ zwischen diesen Geraden der Winkel zwischen den Richtungsvektoren:

${\displaystyle \theta =\arccos {\frac {\mathbf {r_{1}} \cdot \mathbf {r_{2}} }{|\mathbf {r_{1}} ||\mathbf {r_{2}} |}}}$.

Die Geraden sind orthogonal zueinander, wenn der Schnittwinkel ein rechter Winkel ist, also ${\displaystyle \theta =90^{\circ }}$. Das ist genau dann der Fall, wenn das Skalarprodukt der Richtungsvektoren gleich 0 ist, also ${\displaystyle \mathbf {r_{1}} \cdot \mathbf {r_{2}} =0}$.^[4]

Sind zwei Geraden in der Ebene mit ${\displaystyle a_{1}x+b_{1}y=c_{1}}$ und ${\displaystyle a_{2}x+b_{2}y=c_{2}}$ in Koordinatenform gegeben, dann ist der Schnittwinkel ${\displaystyle \theta }$ die Differenz der Neigungswinkel ${\displaystyle \alpha _{1}}$ und ${\displaystyle \alpha _{2}}$ der Geraden:

${\displaystyle \theta =\alpha _{1}-\alpha _{2}}$.

Anwenden des Additionstheorems für den Tangens ergibt

${\displaystyle \tan \theta =\tan(\alpha _{1}-\alpha _{2})={\frac {\tan \alpha _{1}-\tan \alpha _{2}}{1+\tan \alpha _{1}\tan \alpha _{2}}}}$.

Wegen ${\displaystyle \tan \alpha _{1}={\tfrac {a_{1}}{b_{1}}}}$ und ${\displaystyle \tan \alpha _{2}={\tfrac {a_{2}}{b_{2}}}}$ folgt daraus

${\displaystyle {\frac {\tan \alpha _{1}-\tan \alpha _{2}}{1+\tan \alpha _{1}\tan \alpha _{2}}}={\frac {{\frac {a_{1}}{b_{1}}}-{\frac {a_{2}}{b_{2}}}}{1+{\frac {a_{1}a_{2}}{b_{1}b_{2}}}}}={\frac {a_{1}b_{2}-a_{2}b_{1}}{a_{1}a_{2}+b_{1}b_{2}}}}$.

Insgesamt ergibt sich

${\displaystyle \tan \theta ={\frac {a_{1}b_{2}-a_{2}b_{1}}{a_{1}a_{2}+b_{1}b_{2}}}}$.

Anwenden der Umkehrfunktion des Tangens (Arkustangens) auf beiden Seiten der Gleichung ergibt

${\displaystyle \theta =\arctan {\frac {a_{1}b_{2}-a_{2}b_{1}}{a_{1}a_{2}+b_{1}b_{2}}}}$.

Die Geraden sind genau dann orthogonal zueinander, wenn der Nenner gleich 0 ist, also ${\displaystyle a_{1}a_{2}+b_{1}b_{2}=0}$. Für diese Spezialfälle, nämlich für ${\displaystyle \theta =90^{\circ }}$ und ${\displaystyle \theta =-90^{\circ }}$, sind die genannten Gleichungen nicht definiert. Die Funktion ${\displaystyle \tan \theta }$ (Tangens) hat Polstellen bei ${\displaystyle \theta =90^{\circ }}$ und ${\displaystyle \theta =-90^{\circ }}$.^[5]

Schnittwinkel einer Geraden mit einer Ebene

Siehe auch: Schnittwinkel (Geometrie) – Schnittwinkel einer Kurve mit einer Fläche

Der Schnittwinkel ${\displaystyle \alpha }$ zwischen einer Gerade mit dem Richtungsvektor ${\displaystyle {\vec {x}}}$ und einer Ebene mit dem Normalenvektor ${\displaystyle {\vec {n}}}$ ist gegeben durch

${\displaystyle \sin \alpha ={\frac {|{\vec {n}}\cdot {\vec {x}}|}{|{\vec {n}}||{\vec {x}}|}}.}$

• 
  Schnittwinkel ${\displaystyle \alpha }$, Gerade ${\displaystyle g}$, Ebene ${\displaystyle E}$, Projektionsgerade ${\displaystyle p}$ ${\displaystyle {\begin{aligned}&\,\gamma =\beta =90^{\circ }-\alpha \\\Rightarrow \,&\sin(\alpha )=\sin(90^{\circ }-\gamma )=\cos(\gamma )={\frac {|n\cdot x|}{|n||x|}}\end{aligned}}}$
• 
  Schnittwinkel zwischen zwei Ebenen: ${\displaystyle \alpha =\beta =\gamma }$

Schnittwinkel zweier Ebenen

Siehe auch: Schnittwinkel (Geometrie) – Schnittwinkel zweier Flächen

Der Schnittwinkel ${\displaystyle \alpha }$ zwischen zwei Ebenen mit den Normalenvektoren ${\displaystyle {\vec {n}}}$ und ${\displaystyle {\vec {m}}}$ ist entsprechend

${\displaystyle \cos \alpha ={\frac {|{\vec {n}}\cdot {\vec {m}}|}{|{\vec {n}}||{\vec {m}}|}}}$.

Winkelkonstruktion

Einige Winkel kann man allein mit Zirkel und Lineal konstruieren. Dazu gehören der 90-Grad-, 60-Grad-, 72-Grad- und 54-Grad-Winkel, sowie sämtliche Winkel, die durch Verdoppelung, Halbierung, Addition oder Subtraktion (siehe unten) dieser Winkel entstehen.

Die Winkel ${\displaystyle 0^{\circ }<\alpha \leq 180^{\circ }}$ sind in Dezimalgrad als Näherungskonstruktion mithilfe des dritten Strahlensatzes in Kombination mit Zahlengeraden konstruierbar.

Konstruktion des 90-Grad-Winkels (rechten Winkels)

→ Hauptartikel: Rechter Winkel

Man konstruiert genauer gesagt die Senkrechte zu einer bereits gegebenen Strecke ${\displaystyle s}$.

Konstruktion für vorgegebenen Schnittpunkt auf der Geraden

Fällen des Lotes

Konstruktion für vorgegebenen Schnittpunkt auf der Geraden

1. Zeichne einen Kreis um ${\displaystyle P}$ mit beliebigem Radius. Dieser Kreis schneidet ${\displaystyle g}$ in zwei Punkten.
2. Zeichne um diese beiden Punkte jeweils einen Kreis. Die Radien der beiden Kreise müssen so gewählt sein, dass sich die Kreise in zwei Punkten schneiden.
3. Verbinde die beiden Schnittpunkte dieser Kreise durch eine Gerade. Die so gezeichnete Gerade schneidet ${\displaystyle g}$ im rechten Winkel und zwar genau im Punkt ${\displaystyle P}$.

Konstruktion für vorgegebenen Punkt außerhalb der Geraden (Fällen des Lotes)

1. Zeichne einen Kreis um ${\displaystyle P}$ mit einem Radius größer als der Abstand des Punkts von der Geraden. Dieser Kreis schneidet ${\displaystyle g}$ in zwei Punkten.
2. Die weitere Vorgehensweise entspricht der Konstruktion für vorgegebenen Schnittpunkt.

Konstruktion für vorgegebenen Schnittpunkt auf oder außerhalb der Geraden

Konstruktion für vorgegebenen Schnittpunkt auf oder außerhalb der Geraden mithilfe des sogenannten Thaleskreises

1. Wähle einen Punkt ${\displaystyle M}$ in der Nähe des gegebenen Punktes ${\displaystyle P_{1}}$ bzw. ${\displaystyle P_{2}}$ (siehe nebenstehendes Bild).
2. Ziehe einen etwas größeren Halbkreis mit Radius ${\displaystyle |MP_{1}|}$ bzw. ${\displaystyle |MP_{2}|}$, bis dieser die Gerade ${\displaystyle g}$ in ${\displaystyle A}$ schneidet. Falls ${\displaystyle P_{2}}$ gegeben ist, ergibt sich zusätzlich ${\displaystyle P_{1}}$ als Schnittpunkt.
3. Zeichne den Durchmesser des Halbkreises ${\displaystyle |AP_{2}|}$ ein.
4. Die abschließende Gerade durch die Punkte ${\displaystyle P_{1}}$ und ${\displaystyle P_{2}}$ liefert den rechten Winkel am Scheitel ${\displaystyle P_{1}}$.

Konstruktion (ohne vorgegebenen Schnittpunkt)

Bei beliebigem Schnittpunkt entfällt die Festlegung symmetrischer Punkte auf der Geraden

1. Wähle zwei Punkte ${\displaystyle M_{1}}$ und ${\displaystyle M_{2}}$ auf der Geraden, und zu diesen zwei Punkten zwei Kreisradien groß genug, dass die entsprechenden Kreise um ${\displaystyle M_{1}}$ und ${\displaystyle M_{2}}$ sich in zwei Punkten – im Weiteren ${\displaystyle S_{1}}$ und ${\displaystyle S_{2}}$ genannt – schneiden.
2. Zeichne diese beiden Kreise (sie müssen nur soweit gezeichnet werden, dass die beiden Schnittpunkte erkennbar werden).
3. Zeichne die durch die beiden Schnittpunkte ${\displaystyle S_{1}}$ und ${\displaystyle S_{2}}$ gehende Gerade. Diese Gerade ist senkrecht zu ${\displaystyle g}$.

Hinweise

Man muss die Kreise nicht vollständig zeichnen. Es reicht, wenn die Schnittpunkte erkennbar sind. Prinzipiell wird die Konstruktion umso genauer, je größer der Abstand der beiden Schnittpunkte voneinander ist. Denn mit größerem Abstand werden die Auswirkungen von solchen Fehlern kleiner, die dadurch entstehen, dass die neugezeichnete Gerade oder auch schon die gezeichneten Schnittpunkte nicht genau mit den idealen Schnittpunkten übereinstimmen. Andererseits wird die genaue Erkennbarkeit der Schnittpunkte geringer, je flacher sich die Kreise schneiden, was umso mehr der Fall ist, je weiter die Kreisradien von einem Idealradius entfernt sind, bei dem sich die Kreise senkrecht schneiden.

Streckenhalbierung, Mittelsenkrechte

Streckenhalbierung, Mittelsenkrechte

Man halbiert eine gegebene Strecke, indem man die Endpunkte ${\displaystyle A}$ und ${\displaystyle B}$ der Strecke als Mittelpunkte zweier gleicher Kreisbögen wählt und deren zwei gemeinsamen Kreuzungspunkte ${\displaystyle P}$ und ${\displaystyle Q}$ miteinander verbindet. Der dadurch erzeugte Schnittpunkt ${\displaystyle M}$ liefert somit die gesuchte Mitte der Strecke ${\displaystyle {\overline {AB}}}$.

Konstruktion eines 60-Grad-Winkels

Antragen eines 60-Grad-Winkels an eine Gerade in einem gegebenen Scheitelpunkt

1. Ziehe einen Kreis auf der Geraden ${\displaystyle g_{1}}$ um den gegebenen Punkt ${\displaystyle P}$ (Bild 1). Es ergeben sich die zwei Schnittpunkte ${\displaystyle A}$ und ${\displaystyle B}$.
2. Ziehe einen Kreis mit gleichem Radius z. B. um den Schnittpunkt ${\displaystyle B}$ (alternativ um ${\displaystyle A}$) und markiere die Kreuzung der beiden Kreise oberhalb der Geraden ${\displaystyle g_{1}}$ als Schnittpunkt ${\displaystyle C}$.
3. Zeichne eine Gerade ${\displaystyle g_{2}}$ durch den Punkt ${\displaystyle P}$ und den Schnittpunkt ${\displaystyle C}$. Somit schneidet die Gerade ${\displaystyle g_{2}}$ im Scheitelpunkt ${\displaystyle P}$ die Gerade ${\displaystyle g_{1}}$ im Winkel von 60°.

• 
  Bild 1: Antragen eines 60°-Winkels an eine Gerade in einem gegebenen Scheitelpunkt
• 
  Bild 2: Antragen eines 60°-Winkels durch einen Punkt außerhalb der Geraden

Antragen eines 60-Grad-Winkels an eine Gerade durch einen Punkt außerhalb der Geraden

1. Fälle das Lot vom gegebenen Punkt ${\displaystyle P}$ auf die Gerade ${\displaystyle g}$ (Bild 2). Du erhältst die Hilfspunkte ${\displaystyle A}$ und ${\displaystyle B}$ sowie den Gegenpunkt ${\displaystyle C}$. Der Schnittpunkt ist der Fußpunkt ${\displaystyle M}$.
2. Ziehe einen Kreis (${\displaystyle k_{1}}$) um den Fußpunkt durch den gegebenen Punkt.
3. Ziehe mit gleichem Radius einen Kreisbogen (${\displaystyle k_{2}}$) um den Gegenpunkt ${\displaystyle C}$, du bekommst die Punkte ${\displaystyle D}$ und ${\displaystyle E}$, deren Verbindungsgerade die Mittelsenkrechte der Strecke ${\displaystyle {\overline {CM}}}$ ist.
4. Zeichne das gleichseitige Dreieck ${\displaystyle PDE}$. Die an ${\displaystyle P}$ anliegenden Seiten schneiden die Gerade auf gewünschte Weise.

Bild 3: Antragen eines 60°-Winkels an eine Gerade durch einen Punkt außerhalb der Geraden, auch möglich mithilfe eines sogenannten kollabierenden Zirkels

Die nebenstehende Abbildung (Bild 3) zeigt eine alternative Vorgehensweise, die neben dem gegebenen Punkt ${\displaystyle P}$ und der gegebenen Geraden ${\displaystyle g_{1}}$ nur vier Kreise mit gleichem Radius und die Gerade ${\displaystyle g_{2}}$ für die Lösung benötigt. Im Verlauf der Konstruktion werden für das Ziehen eines Kreises stets zwei Punkte genutzt. Der Abstand der beiden Punkte ist gleich dem Kreisradius, aufgrund dessen könnte auch ein sogenannter euklidischer oder kollabierender Zirkel eingesetzt werden.

1. Ziehe einen Kreis mit einem beliebigen Radius um ${\displaystyle P}$, es ergibt den Schnittpunkt ${\displaystyle A}$ auf der Geraden ${\displaystyle g_{1}}$.
2. Ziehe den zweiten Kreis um Punkt ${\displaystyle A}$ durch ${\displaystyle P}$ sowie den dritten Kreis um den soeben erzeugten Punkt ${\displaystyle B}$ auf ${\displaystyle g_{1}}$ durch ${\displaystyle A}$, er schneidet den Kreis um ${\displaystyle P}$ in ${\displaystyle C}$. Die Abstände von den Punkten ${\displaystyle P}$ und ${\displaystyle C}$ zu der Geraden ${\displaystyle g_{1}}$ sind gleich.
3. Schließlich ziehe den vierten Kreis um ${\displaystyle C}$ durch ${\displaystyle P}$, der den Kreis um ${\displaystyle P}$ in ${\displaystyle D}$ schneidet, und zeichne die Gerade ${\displaystyle g_{2}}$ durch die Punkte ${\displaystyle P}$ und ${\displaystyle D}$. Sie schneidet die Gerade ${\displaystyle g_{1}}$ im Scheitelpunkt ${\displaystyle E}$ und liefert somit den Winkel ${\displaystyle AED}$ mit der gesuchten Winkelweite 60°.

Konstruktion eines 45-Grad-Winkels

Antragen eines 45-Grad-Winkels an eine Gerade in einem gegebenen Scheitelpunkt

Eine der kürzesten Lösungen wird mit der Konstruktion des 90-Grad-Winkels als Basis (Bild 4) erreicht.

1. Bestimme den Punkt ${\displaystyle P}$ beliebig auf der Geraden ${\displaystyle g_{1},}$ ziehe einen Kreis mit dem Radius ${\displaystyle |AP|}$ um ${\displaystyle A}$ und markiere den Schnittpunkt ${\displaystyle B}$ auf der Geraden ${\displaystyle g_{1}.}$
2. Ziehe den Kreisbogen mit Radius ${\displaystyle |BP|}$ um ${\displaystyle B.}$
3. Ziehe den Kreisbogen mit gleichem Radius um ${\displaystyle P}$ und markiere den Schnittpunkt der beiden mit ${\displaystyle C.}$
4. Verbinde den Punkt ${\displaystyle A}$ mit ${\displaystyle C}$, ${\displaystyle D}$ ist der Schnittpunkt mit dem Kreis um ${\displaystyle A.}$.
5. Die abschließende Halbgerade ${\displaystyle g_{2}}$, ab dem Punkt ${\displaystyle P}$ durch ${\displaystyle D}$, liefert den Winkel ${\displaystyle APD}$ mit der gesuchten Winkelweite ${\displaystyle 45^{\circ }.}$

• 
  Bild 4: Antragen eines 45°-Winkels an eine Gerade in einem gegebenen Scheitelpunkt, auch möglich mithilfe eines kollabierenden Zirkels
• 
  Bild 5: Antragen eines 45°-Winkels an eine Gerade durch einen Punkt außerhalb der Geraden, auch möglich mithilfe eines kollabierenden Zirkels

Antragen eines 45-Grad-Winkels an eine Gerade durch einen Punkt außerhalb der Geraden

1. Ziehe einen Kreis um den gegebenen Punkt ${\displaystyle P}$ mit dem beliebigen Radius ${\displaystyle |PA|}$ und markiere den Schnittpunkt ${\displaystyle B}$ auf ${\displaystyle g_{1}}$.
2. Ziehe den zweiten Kreis mit gleichem Radius um ${\displaystyle A}$ und markiere den Schnittpunkt ${\displaystyle C}$ auf ${\displaystyle g_{1}}$.
3. Um den Punkt ${\displaystyle C}$ folgt der dritte Kreis mit gleichem Radius; ${\displaystyle D}$ ist der Schnittpunkt mit dem Kreis um ${\displaystyle P}$.
4. Der vierte Kreis mit gleichem Radius hat den Mittelpunkt ${\displaystyle D}$; ${\displaystyle E}$ ist der Schnittpunkt mit ${\displaystyle g_{1}}$.
5. Ziehe den fünften und letzten Kreis mit gleichem Radius um ${\displaystyle E}$; ${\displaystyle F}$ ist der Schnittpunkt mit dem Kreis um ${\displaystyle C}$.
6. Verbinde den Punkt ${\displaystyle D}$ mit ${\displaystyle F}$; ${\displaystyle G}$ ist der Schnittpunkt mit dem Kreis um ${\displaystyle D}$.
7. Die abschließende Halbgerade ${\displaystyle g_{2}}$, ab dem Punkt ${\displaystyle P}$ durch ${\displaystyle G}$, liefert den Winkel ${\displaystyle CHG}$ mit der gesuchten Winkelweite ${\displaystyle 45^{\circ }}$.

Konstruktion eines 30-Grad-Winkels

Der erste Gedanke ist vielleicht, die Konstruktionen des 60-Grad-Winkels zu verwenden, um den 30-Grad-Winkel durch einfache Halbierung des 60-Grad-Winkels zu erreichen. Die ersten beiden im Folgenden beschriebenen Vorgehensweisen zeigen aber, es geht auch mit weniger Konstruktionsschritten.

Antragen eines 30-Grad-Winkels an eine Gerade in einem gegebenen Scheitelpunkt

1. Bestimme den Punkt ${\displaystyle A}$ beliebig auf der Geraden ${\displaystyle g_{1}}$ und ziehe einen Kreis um ${\displaystyle A}$ durch den gegebenen Punkt ${\displaystyle P}$ (siehe Bild 6). Es ergibt sich der Schnittpunkt ${\displaystyle B}$.
2. Ziehe einen Kreis mit gleichem Radius um ${\displaystyle B}$ und markiere die Kreuzung der beiden Kreise oberhalb der Geraden ${\displaystyle g_{1}}$ als Schnittpunkt ${\displaystyle C}$.
3. Zeichne eine Gerade ${\displaystyle g_{2}}$ durch den Punkt ${\displaystyle P}$ und den Schnittpunkt ${\displaystyle C}$. Somit schneidet die Gerade ${\displaystyle g_{2}}$ im Scheitelpunkt ${\displaystyle P}$ die Gerade ${\displaystyle g_{1}}$ im Winkel von 30°.

Bild 6: Antragen eines 30°-Winkels an eine Gerade ${\displaystyle g_{1}}$ in einem gegebenen Scheitelpunkt ${\displaystyle P}$

Antragen eines 30-Grad-Winkels an eine Gerade durch einen Punkt außerhalb der Geraden

1. Fälle das Lot vom gegebenen Punkt ${\displaystyle P}$ auf die Gerade ${\displaystyle g_{1}}$ folgendermaßen (siehe Bild 7): Mit einem beliebigen Radius um ${\displaystyle P}$ ergeben sich die Hilfspunkte ${\displaystyle A}$ und ${\displaystyle B}$, zwei kleine Kreisbögen mit dem Radius ${\displaystyle {\overline {AP}}}$ um ${\displaystyle A}$ bzw. ${\displaystyle B}$ schneiden sich im Gegenpunkt ${\displaystyle C}$. Die Verbindung ${\displaystyle P}$ mit ${\displaystyle C}$ liefert den Fußpunkt ${\displaystyle D.}$
2. Ziehe einen Kreisbogen mit dem Radius ${\displaystyle {\overline {CD}}}$ um den Gegenpunkt ${\displaystyle C}$ und einen mit gleichem Radius um den Fußpunkt ${\displaystyle D}$, dabei ergibt sich der Punkt ${\displaystyle E.}$
3. Verbinde den Punkt ${\displaystyle P}$ mit ${\displaystyle E}$, dabei ergibt sich der Punkt ${\displaystyle F}$ und am Scheitel ${\displaystyle P}$ der Winkel 30°.
4. Ziehe einen Kreisbogen mit dem Radius ${\displaystyle {\overline {FP}}}$ um den Punkt ${\displaystyle F,}$ Schnittpunkt mit ${\displaystyle g_{1}}$ ist ${\displaystyle G}$.
5. Ziehe einen Halbkreis mit dem Radius ${\displaystyle {\overline {GF}}}$ um den Punkt ${\displaystyle G}$, Schnittpunkt mit ${\displaystyle g_{1}}$ ist ${\displaystyle H}$. Die abschließende Gerade ${\displaystyle g_{2}}$ durch ${\displaystyle H}$ und ${\displaystyle P}$ liefert am Scheitel ${\displaystyle H}$ den Winkel ${\displaystyle FHP}$ mit der Winkelweite 30°.

• 
  Bild 7: Antragen eines 30°-Winkels durch einen Punkt ${\displaystyle P}$ außerhalb der Geraden ${\displaystyle g_{1}}$
• 
  Bild 8: Antragen eines 30°-Winkels an eine Gerade ${\displaystyle g_{1}}$ durch einen Punkt ${\displaystyle P}$ außerhalb der Geraden ${\displaystyle g_{1}}$, auch möglich mithilfe eines kollabierenden Zirkels

Die Darstellung im Bild 8 zeigt eine alternative Vorgehensweise. Sie benötigt für die Lösung, neben dem gegebenen Punkt ${\displaystyle P}$ und der gegebenen Geraden ${\displaystyle g_{1}}$, nur fünf Kreise mit gleichem Radius und die Gerade ${\displaystyle g_{2}}$. Die Konstruktion ist eine Weiterführung der Konstruktion des 60-Grad-Winkels (Bild 3). Dafür bedarf es nur noch des fünften Kreises, gezogen um Punkt ${\displaystyle D}$ durch ${\displaystyle P}$, und schließlich der Geraden ${\displaystyle g_{2}}$ durch die Punkte ${\displaystyle P}$ und ${\displaystyle E}$. Die Gerade ${\displaystyle g_{2}}$ schneidet die Gerade ${\displaystyle g_{1}}$ im Scheitelpunkt ${\displaystyle F}$ und liefert somit den Winkel ${\displaystyle AFP}$ mit der gesuchten Winkelweite 30°.

Konstruktion eines 72-, 54- oder 18-Grad-Winkels

Die etwas exotischere Konstruktion dieser drei Winkel findet man im regelmäßigen Fünfeck.

Winkel 72°, 54° und 18° im Fünfeck, ${\displaystyle {\overline {EF}}={\overline {EC}}}$, ${\displaystyle {\overline {BH}}={\overline {CG}}}$

Addition und Subtraktion von Winkeln

Winkelweite ${\displaystyle \alpha _{1}}$ und ${\displaystyle \alpha _{2}}$

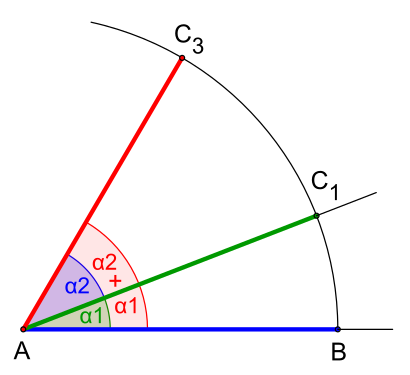
Jeder Winkel lässt sich zu einem anderen Winkel konstruktiv, sprich geometrisch, addieren und subtrahieren. Mit anderen Worten, möchte man z. B. (siehe drei Bilder) einen Winkel um die Größe eines anderen vermehren bzw. vermindern, so zeichnet man zunächst um die Scheitelpunkte der Winkel jeweils einen für beide Winkel gleich großen Kreisbogen, der beide Schenkel des jeweiligen Winkels schneidet oder berührt.

Winkel addieren

Zuerst wird der Kreisbogen ${\displaystyle ABC_{1}}$ des ersten Winkels ${\displaystyle BAC_{1}}$ über ${\displaystyle C_{1}}$ hinaus verlängert, damit darauf auch der zweite Winkel ${\displaystyle BAC_{2}}$ genügend Platz findet. Nun nimmt man die Winkelweite ${\displaystyle \alpha _{2}}$ am Abstand ${\displaystyle |BC_{2}|}$ in den Zirkel und überträgt sie damit, ab dem Schnittpunkt ${\displaystyle C_{1}}$, auf den verlängerten Kreisbogen. Es ergibt sich der Schnittpunkt ${\displaystyle C_{3}}$. Abschließend wird der neue Winkelschenkel ${\displaystyle {\overline {AC_{3}}}}$ eingezeichnet.

Der somit durch geometrische Addition erzeugte Summenwinkel ${\displaystyle BAC_{3}}$ hat die Winkelweite ${\displaystyle \alpha _{1}+\alpha _{2}}$.

• 
  Addition, Winkelweiten ${\displaystyle \alpha _{1}+\alpha _{2}}$
• 
  Subtraktion, Winkelweiten ${\displaystyle \alpha _{2}-\alpha _{1}}$

Winkel subtrahieren

Um den kleineren Winkel ${\displaystyle BAC_{1}}$ vom größeren Winkel ${\displaystyle BAC_{2}}$ zu subtrahieren (Bild: Winkelweite ${\displaystyle \alpha _{1}}$ und ${\displaystyle \alpha _{2}}$), nimmt man die Winkelweite ${\displaystyle \alpha _{1}}$ am Abstand ${\displaystyle |BC_{1}|}$ in den Zirkel und überträgt sie damit, ab dem Schnittpunkt ${\displaystyle C_{2}}$, auf den Kreisbogen ${\displaystyle ABC_{2}}$. Es ergibt sich der Schnittpunkt ${\displaystyle C_{3}}$. Abschließend wird der neue Winkelschenkel ${\displaystyle {\overline {AC_{3}}}}$ eingezeichnet.

Der somit durch geometrische Subtraktion erzeugte Differenzwinkel ${\displaystyle BAC_{3}}$ hat die Winkelweite ${\displaystyle \alpha _{2}-\alpha _{1}}$.

Winkelteilungen

Winkelhalbierung

Winkelhalbierende (rot)

Ein Winkel besteht stets aus zwei Schenkeln, die sich im Scheitelpunkt treffen. Zieht man nun zwei gleich große Kreise auf je einem Schenkel durch den Scheitelpunkt, so bildet die Strecke zwischen den Kreisschnittpunkten die Winkelhalbierende. Jeder Punkt auf der Winkelhalbierenden ist gleich weit von den Schenkeln entfernt.

Konstruktion

Der zuerst gezeichnete Kreisbogen um den Scheitelpunkt ${\displaystyle A}$, mit einem beliebigen Radius, schneidet die Schenkel des Winkels in ${\displaystyle B}$ bzw. ${\displaystyle C}$. Nun wird, entweder mit der gleichen (siehe Bild) oder mit geänderter Zirkelöffnung, um die Schnittpunkte ${\displaystyle B}$ und ${\displaystyle C}$ jeweils ein gleich großer Kreisbogen geschlagen. Abschließend zieht man ab dem Scheitelpunkt ${\displaystyle A}$, durch den zuletzt entstandenen Schnittpunkt ${\displaystyle D}$, eine Halbgerade und erhält somit die Winkelhalbierende.

Dreiteilung

→ Hauptartikel: Dreiteilung des Winkels

Dreiteilung des Winkels nach Bieberbach

Die allgemeine Dreiteilung des Winkels ist mit euklidischen Werkzeugen nicht möglich. Jedoch liegen (Hand-)Zeichengeräte (z. B. Geodreieck) für diese Aufgabe vor. Was allerdings auch möglich ist, sind Näherungskonstruktionen mit geringen Winkelfehlern.

Beliebige Teilung

Die beliebige Teilung erfordert ein Hilfsmittel, mit dem ein Winkel proportional auf eine Strecke abgebildet werden kann und umgekehrt, beispielsweise eine Schablone, mit einer als Archimedische Spirale oder Quadratrix des Hippias geformten Kante. Damit lässt sich eine Winkelteilung in eine Streckenteilung überführen. Anwendung findet man in der Konstruktion bestimmter regelmäßiger Polygone, die allein mit Zirkel und Lineal nicht konstruierbar sind, wie z. B. des Elfecks.

Folgerung (allgemeine Winkelkonstruktionen) und große Winkeltabelle

Beispiele für konstruierbare Winkel mit Basis 3°:
Für den Winkel 9° und 3° bedarf es lediglich der Konstruktion des Winkels 30° und der des regelmäßigen Fünfecks.

Konstruiert man die obigen Winkel (90°, 60°, 72° oder 54° oder deren Summen bzw. Differenzen), so lassen sich aus diesen per Winkelhalbierung weitere Winkel (45°, 30°, 36° und 27° oder den zugehörigen Summen bzw. Differenzen) konstruieren, die und deren Abkömmlinge sich wieder halbieren lassen. Den Winkel von 3° erhält man z. B. durch folgende Vorgehensweise: ${\displaystyle 72^{\circ }/2\rightarrow 36^{\circ }/2\rightarrow 18^{\circ }-15^{\circ }=3^{\circ }}$. Generell lassen sich alle Winkel konstruieren, deren Sinus (und damit auch deren Kosinus) durch einen mathematischen Ausdruck dargestellt werden kann, der nur aus ganzen Zahlen, Grundrechenarten und Quadratwurzeln besteht. Das gilt z. B. für ganzzahlige Winkel (Gradmaß), die ein Vielfaches von 3° sind:^[6]

• ${\displaystyle \sin(0^{\circ })=\cos(90^{\circ })=0}$
• ${\displaystyle \sin(3^{\circ })=\cos(87^{\circ })={\frac {1}{16}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {3}}+1\right)\cdot \left({\sqrt {5}}-1\right)-2\cdot \left({\sqrt {3}}-1\right)\cdot {\sqrt {5+{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(6^{\circ })=\cos(84^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot {\sqrt {3}}\cdot {\sqrt {5-{\sqrt {5}}}}-\left({\sqrt {5}}+1\right)\right)}$
• ${\displaystyle \sin(9^{\circ })=\cos(81^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)-2\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(12^{\circ })=\cos(78^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot {\sqrt {5+{\sqrt {5}}}}-{\sqrt {3}}\cdot \left({\sqrt {5}}-1\right)\right)}$
• ${\displaystyle \sin(15^{\circ })=\cos(75^{\circ })={\frac {1}{4}}\cdot {\sqrt {2}}\cdot \left({\sqrt {3}}-1\right)}$
• ${\displaystyle \sin(18^{\circ })=\cos(72^{\circ })={\frac {1}{4}}\cdot \left({\sqrt {5}}-1\right)}$
• ${\displaystyle \sin(21^{\circ })=\cos(69^{\circ })={\frac {1}{16}}\cdot \left(-{\sqrt {2}}\cdot \left({\sqrt {3}}-1\right)\cdot \left({\sqrt {5}}+1\right)+2\cdot \left({\sqrt {3}}+1\right)\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(24^{\circ })=\cos(66^{\circ })={\frac {1}{8}}\cdot \left(-{\sqrt {2}}\cdot {\sqrt {5-{\sqrt {5}}}}+{\sqrt {3}}\cdot \left({\sqrt {5}}+1\right)\right)}$
• ${\displaystyle \sin(27^{\circ })=\cos(63^{\circ })={\frac {1}{8}}\cdot \left(-{\sqrt {2}}\cdot \left({\sqrt {5}}-1\right)+2\cdot {\sqrt {5+{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(30^{\circ })=\cos(60^{\circ })={\frac {1}{2}}}$
• ${\displaystyle \sin(33^{\circ })=\cos(57^{\circ })={\frac {1}{16}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {3}}+1\right)\cdot \left({\sqrt {5}}-1\right)+2\cdot \left({\sqrt {3}}-1\right)\cdot {\sqrt {5+{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(36^{\circ })=\cos(54^{\circ })={\frac {1}{4}}\cdot {\sqrt {2}}\cdot {\sqrt {5-{\sqrt {5}}}}}$
• ${\displaystyle \sin(39^{\circ })=\cos(51^{\circ })={\frac {1}{16}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {3}}+1\right)\cdot \left({\sqrt {5}}+1\right)-2\cdot \left({\sqrt {3}}-1\right)\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(42^{\circ })=\cos(48^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot {\sqrt {3}}\cdot {\sqrt {5+{\sqrt {5}}}}-\left({\sqrt {5}}-1\right)\right)}$
• ${\displaystyle \sin(45^{\circ })=\cos(45^{\circ })={\frac {1}{2}}\cdot {\sqrt {2}}}$
• ${\displaystyle \sin(48^{\circ })=\cos(42^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot {\sqrt {5+{\sqrt {5}}}}+{\sqrt {3}}\cdot \left({\sqrt {5}}-1\right)\right)}$
• ${\displaystyle \sin(51^{\circ })=\cos(39^{\circ })={\frac {1}{16}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {3}}-1\right)\cdot \left({\sqrt {5}}+1\right)+2\cdot \left({\sqrt {3}}+1\right)\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(54^{\circ })=\cos(36^{\circ })={\frac {1}{4}}\cdot \left({\sqrt {5}}+1\right)}$
• ${\displaystyle \sin(57^{\circ })=\cos(33^{\circ })={\frac {1}{16}}\cdot \left(-{\sqrt {2}}\cdot \left({\sqrt {3}}-1\right)\cdot \left({\sqrt {5}}-1\right)+2\cdot \left({\sqrt {3}}+1\right)\cdot {\sqrt {5+{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(60^{\circ })=\cos(30^{\circ })={\frac {1}{2}}\cdot {\sqrt {3}}}$
• ${\displaystyle \sin(63^{\circ })=\cos(27^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {5}}-1\right)+2\cdot {\sqrt {5+{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(66^{\circ })=\cos(24^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot {\sqrt {3}}\cdot {\sqrt {5-{\sqrt {5}}}}+\left({\sqrt {5}}+1\right)\right)}$
• ${\displaystyle \sin(69^{\circ })=\cos(21^{\circ })={\frac {1}{16}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {3}}+1\right)\cdot \left({\sqrt {5}}+1\right)+2\cdot \left({\sqrt {3}}-1\right)\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(72^{\circ })=\cos(18^{\circ })={\frac {1}{4}}\cdot {\sqrt {2}}\cdot {\sqrt {5+{\sqrt {5}}}}}$
• ${\displaystyle \sin(75^{\circ })=\cos(15^{\circ })={\frac {1}{4}}\cdot {\sqrt {2}}\cdot \left({\sqrt {3}}+1\right)}$
• ${\displaystyle \sin(78^{\circ })=\cos(12^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot {\sqrt {3}}\cdot {\sqrt {5+{\sqrt {5}}}}+\left({\sqrt {5}}-1\right)\right)}$
• ${\displaystyle \sin(81^{\circ })=\cos(9^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)+2\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(84^{\circ })=\cos(6^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot {\sqrt {5-{\sqrt {5}}}}+{\sqrt {3}}\cdot \left({\sqrt {5}}+1\right)\right)}$
• ${\displaystyle \sin(87^{\circ })=\cos(3^{\circ })={\frac {1}{16}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {3}}-1\right)\cdot \left({\sqrt {5}}-1\right)+2\cdot \left({\sqrt {3}}+1\right)\cdot {\sqrt {5+{\sqrt {5}}}}\right)}$
• ${\displaystyle \sin(90^{\circ })=\cos(0^{\circ })=1}$

Die Winkelhalbierung kann durch Substitution der Halbwinkelformeln

${\displaystyle \sin {\frac {\alpha }{2}}={\sqrt {\frac {1-\cos \alpha }{2}}}}$ und ${\displaystyle \cos {\frac {\alpha }{2}}={\sqrt {\frac {1+\cos \alpha }{2}}}}$

ausgedrückt werden. Das Antragen eines Winkels an einen anderen kann durch Substitution der Additionstheoreme

${\displaystyle \sin(\alpha \pm \beta )=\sin \alpha \;\cos \beta \pm \cos \alpha \;\sin \beta }$ und ${\displaystyle \cos(\alpha \pm \beta )=\cos \alpha \;\cos \beta \mp \sin \alpha \;\sin \beta }$

ausgedrückt werden.

Darüber hinaus hat der Kosinus des Zentriwinkel des 17-Ecks noch den Wert:

${\displaystyle \cos {\frac {360^{\circ }}{17}}={\frac {1}{16}}\left(-1+{\sqrt {17}}+{\sqrt {2\left(17-{\sqrt {17}}\right)}}+2{\sqrt {17+3{\sqrt {17}}-{\sqrt {2\left(17-{\sqrt {17}}\right)}}-2{\sqrt {2\left(17+{\sqrt {17}}\right)}}}}\right)\ \approx 0{,}93247222940435580457}$,

woraus sich seine Konstruierbarkeit ergibt.

Winkelmessung

→ Hauptartikel: Winkelmessung

Bei der Winkelmessung wird mit Hilfe technischer Einrichtungen ermittelt, in welchem Winkel zwei Geraden oder zwei sonstige Richtungen zueinander stehen.

Kreiswinkel

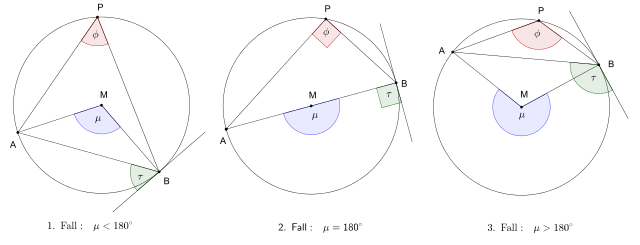
→ Hauptartikel: Kreiswinkel

Am Kreis liegen verschiedene besondere Winkel, die in der klassischen zweidimensionalen Geometrie wichtig sind, vor, zum Beispiel der Umfangswinkel, Mittelpunktswinkel und der Sehnentangentenwinkel. Wichtige Sätze über diese Winkel sind der Kreiswinkelsatz, Umfangswinkelsatz und Sehnentangentenwinkelsatz.

Umfangswinkel, Mittelpunktswinkel und Sehnentangentenwinkel

Weblinks

Wiktionary: Winkel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Winkel – Sammlung von Bildern, Videos und Audiodateien

• class=skin-invert-image|Näherungskonstruktion eines Winkels in Dezimalgrad mittels des dritten Strahlensatzes
• Winkel für Schüler erklärt. mathematik-wissen.de

Einzelnachweise

1. Klaus Fritzsche: Grundlagen der Schulgeometrie. (PDF) Universität Wuppertal, Fachbereich C, 2010, S. 2, abgerufen am 22. Mai 2020.
2. Winkelpaare, Normalwinkel. Pädagogische Hochschule Tirol, Österreich, S. 2, abgerufen am 5. August 2021.
3. The trigonometry arctan() function - inverse tangent - math word definition - Math Open Reference. Abgerufen am 16. Februar 2023.
4. Tutorials List. Abgerufen am 16. Februar 2023 (englisch).
5. Angle of Intersection of Two Lines | eMathZone. 28. Januar 2015, abgerufen am 16. Februar 2023 (amerikanisches Englisch).
6. Cos/Sin: Joachim Mohr Mathematik Musik Pascal Delphi. Abgerufen am 16. Februar 2023.