Statische Bestimmtheit

Statische Bestimmtheit ist ein Begriff der Statik. Er charakterisiert die Lagerung ruhender Körper und den inneren Aufbau von Körpersystemen wie z. B. Fachwerke sowie die Lösbarkeit der mit ihr verbundenen Gleichgewichts-Aufgabe mit den Mitteln der Starrkörpermechanik.^[1][2]

Lagerungen können grundsätzlich statisch bestimmt, unbestimmt oder überbestimmt sein. Die statische Bestimmtheit ist bei der Konzipierung von Konstruktionen von Bedeutung, vor allem in der Baustatik, in der Maschinentechnik und im Apparatebau. Statisch bestimmt gelagerte Körper bzw. statisch bestimmte Körpersysteme ertragen geometrische Einflüsse wie Wärmedehnungen, kleine Lagerverschiebungen, Herstellungs- und Montageungenauigkeiten usw. ohne Zwängungen und damit verbundene Kräfte, wie dies z. B. für Brücken und andere Tragwerke wesentlich sein kann.

Statische Bestimmtheit und Lagerung

Statische Bestimmtheit: Determinante

Statisch bestimmte Lagerung

Statisch bestimmt ist die Lagerung eines Körpers, wenn die unbekannten Lagerreaktionen (Kräfte und Momente) mit den Gleichgewichts-Bedingungen allein berechnet oder mit den Mitteln der graphischen Statik bestimmt werden können.^[3][4][5] Eine statisch bestimmte Lagerung ist bewegungsgeometrisch eindeutig und damit auch kinematisch bestimmt.^[3][6] Dies bedeutet, dass die Lagerung jeden der Bewegungsfreiheitsgrade des Körpers genau einmal einschränkt. Bei räumlichen Problemen sind es 6 Freiheitsgrade (je 3 Translationen und Rotationen), bei ebenen Problemen sind es 3 Freiheitsgrade (2 Translationen, 1 Rotation). Die einzelnen Lager tragen zu dieser entsprechend ihrer Wertigkeit mit Lagerreaktionen (Kräften und/oder Momenten) bei.^[6][7] Die Wertigkeit drückt die Anzahl Freiheitsgrade aus, die durch das betreffende Lager eingeschränkt werden. Jede Einschränkung eines Freiheitsgrades wird mathematisch durch eine entsprechende Gleichgewichtsbedingung ausgedrückt. Diese verknüpfen die als bekannt geltenden äußeren Belastungen (Kräfte und Momente) mit den unbekannten Lagerreaktionen und bilden ein lineares, homogenes Gleichungssystem. Statische Bestimmtheit verlangt als notwendige und hinreichende Bedingung, dass die Koeffizientenmatrix der unbekannten Lagerreaktionen quadratisch ist, und dass ihre Determinante ungleich Null ist. Dies trifft zu, wenn die Gleichgewichtsbedingungen voneinander linear unabhängig sind.^[3][7][8]

Statisch unbestimmte Lagerung

Schränkt die Lagerung einzelne Freiheitsgrade mehrfach ein, so enthält das Gleichungssystem mehr unbekannte Lagerreaktionen als Gleichgewichtsbedingungen; es ist mit letzteren allein nicht lösbar. Die Lagerung ist somit statisch unbestimmt^[9], aber wegen der Überzahl an bewegungsgeometrischen Bedingungen gleichzeitig auch geometrisch bzw. kinematisch überbestimmt.^[3][10] In solchen Fällen kann der Zusammenhang zwischen Belastung und Verformung des Körpers weitere Gleichungen liefern.^[6][10][11]

Aus einem statisch unbestimmt gelagerten Körper kann durch geeignete Unterteilung und Verbindung mittels Gelenken ein statisch bestimmtes Körpersystem erzeugt werden. Jedes eingefügte Gelenk erhöht den Freiheitsgrad bei ebenen Problemen um 1 bzw. bei räumlichen Problemen je nach Art des Gelenks um 1 bis 3. Einfache Beispiele hierfür sind der Gerberträger und der Dreigelenkbogen. Auch mit jedem plastischen Dreh- oder Verschiebungsgelenk wird der Grad der statischen Unbestimmtheit eines Körpers reduziert. Dies wird beim Traglastverfahren^[2] ausgenutzt, um die maximale Belastbarkeit eines Tragwerks bis zum Erreichen eines verschieblichen, also statisch überbestimmten Systems zu ermitteln.^[12] Bei einer statisch unbestimmten Lagerung können die elastischen Bauteilverformungen reduziert werden, und eine Beeinträchtigung der Lagerung führt nicht zwingend zum vollständigen Funktionsausfall.^[12]

Statisch überbestimmte Lagerung

Sind umgekehrt einzelne Freiheitsgrade nicht eingeschränkt, bestehen mehr Gleichgewichtsbedingungen als unbekannte statische Größen. Dann ist die Lagerung statisch überbestimmt bzw. kinematisch unbestimmt.^[6] Eine solche Situation liegt bei Bauteilen vor, deren Funktion eine bestimmte Beweglichkeit verlangt, z. B. die Rotation um die Körperachse bei einer Antriebswelle oder die freie Drehbarkeit eines Turmdrehkrans um die vertikale Achse bei Betriebsruhe, um das Schwenken in die Windrichtung zu ermöglichen. Ansonsten aber sind statisch überbestimmte, also verschiebliche Systeme für die Aufnahme statischer Kräfte ungeeignet.^[13][14]

Beurteilung

In einfacheren Fällen kann mit technischem Sachverstand die statische Bestimmtheit durch eine qualitative, anschauliche Betrachtung beurteilt werden. Statisch bestimmte Konstruktionen lassen sich zwangsfrei zu einem unbeweglichen System aufbauen. Zur Beurteilung der statischen Bestimmtheit eines Körpers oder eines Körpersystems können auch geeignete Abzählformeln hilfreich sein. Zusätzlich zur statischen Bestimmtheit ist es sinnvoll, auch die technische Brauchbarkeit bzw. Tauglichkeit zu betrachten. Nicht jede statisch bestimmte Konstruktion ist zugleich brauchbar.

Um die Begriffe statisch unbestimmt und statisch überbestimmt bzw. kinematisch überbestimmt und kinematisch unbestimmt ist in jüngerer Zeit einige Verwirrung entstanden, indem sie entgegen ihrer klassischen Definition im deutschsprachigen Schrifttum vereinzelt auch umgekehrt^[15] oder vermischt gehandhabt werden.^[7]

Grad der statischen Bestimmtheit

Statische Bestimmtheit: Beispiele

Ein wichtiges Beurteilungskriterium ist der Grad der statischen Bestimmtheit^[16] bzw. etwas weniger allgemein Grad der statischen Unbestimmtheit^[13][14]. Er charakterisiert die Lagerung eines Körpers oder Körpersystems sowie dessen innerer Aufbau quantitativ. Diese ganzzahlige Kenngröße ${\displaystyle n}$ besteht beim einzelnen Körper aus der Differenz zwischen der Zahl ${\displaystyle r}$ unbekannter statischer Größen (Lagerreaktionen) und der Anzahl ${\displaystyle f}$ Gleichgewichtsbedingungen:

${\displaystyle n=r-f}$

Aus kinematischer Sicht bedeuten ${\displaystyle f}$ der Freiheitsgrad des frei beweglichen Körpers und ${\displaystyle r}$ die Anzahl konstruktionsseitig eingeschränkter Freiheitsgrade.

${\displaystyle n=0}$: statisch und kinematisch bestimmt, sofern jeder Freiheitsgrad genau einmal eingeschränkt ist,

${\displaystyle n>0}$: n-fach statisch unbestimmt bzw. kinematisch überbestimmt,

${\displaystyle n<0}$: n-fach statisch überbestimmt bzw. kinematisch unbestimmt, d. h. verschieblich.

In der Literatur wird die rechte Seite der obigen Formel und damit der Grad der statischen Bestimmtheit jedoch auch mit vertauschten Vorzeichen dargestellt.^[17]

Die Bedingung ${\displaystyle n=0}$ ist für die statische Bestimmtheit notwendig, aber nicht hinreichend. Denn es ist möglich, dass einzelne Freiheitsgrade nicht eingeschränkt sind, andere aber mehrfach. Dann ist die Koeffizientendeterminante der Gleichgewichtsbedingungen Null, und die Lagerung ist weder statisch noch kinematisch bestimmt.

Aufbau/Abbaukriterium

Beim Aufbaukriterium ist es zielführend von einem statisch bestimmten Grundsystem auszugehen und durch Ergänzen/Entfernen von Bindungswertigkeiten/Lagerreaktionen das gewünschte System zu bekommen.^[18] Hierbei startet man üblicherweise bei einem

• Träger auf zwei Stützen
• einem Kragarm
• Einem Dreigelenkrahmen
• einem dreieckigen Fachwerk aus drei gelenkig verbundenen Stäben

• 
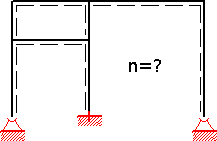
  Statisch unbestimmtes System mit Freiheitsgrad n > 0
• 
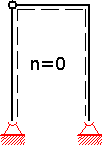
  Statisch bestimmtes Grundsystem
• 
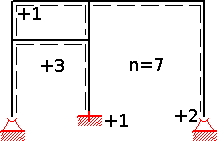
  Statisch bestimmtes Grundsystem mit Kragarmen
• 
  Man fügt 7 Lagewertigkeiten hinzu.

Beispiel: Bei einem System ist der Grad der statischen Unbestimmtheit gesucht. Es wird ein (ähnliches) statisch bestimmtes Grundsystem gewählt und anschließend statisch bestimmte Kragarme hinzugefügt. Man fügt Bindungen und Lagerreaktionen hinzu (bzw. bei kinematischen Systemen entfernt sie) und zählt ihre Wertigkeit zusammen.

Allgemeines Abzählkriterium

Die Bestimmung von n kann mit der folgenden, als Abzählkriterium bekannten Formel erfolgen:^[19][20][21]

ebene Tragwerke: ${\displaystyle n=a+z-3t\ ,}$

räumliche Tragwerke: ${\displaystyle n=a+z-6t\ .}$

Hierbei sind:

${\displaystyle a}$ : Anzahl der möglichen Auflagerkräfte (Wertigkeiten der Auflager)

${\displaystyle z}$ : Anzahl der möglichen Zwischenkräfte (Wertigkeiten der Verbindungen),

${\displaystyle t}$ : Anzahl der starren Bauteile/Träger.

durch Umformen bekommt man auch folgende alternative Formel:

${\displaystyle n=a_{\text{Reaktionen}}+3\cdot (t_{\text{Felder}}-k_{\text{Knoten}})-r_{\text{Gelenke}}}$^[22]

mit

• ${\displaystyle a}$: Anzahl der möglichen Auflagerkräfte (Wertigkeiten der Auflager)
• ${\displaystyle t}$: Anzahl der Abschnitte des Durchlaufträgers zwischen den für ${\displaystyle k}$ gezählten Punkten
• ${\displaystyle k}$: Anzahl der Knoten/Stabenden
• ${\displaystyle r}$: Anzahl der nicht unterbundenen Relativbewegungen zwischen den verbundenen Stäben

Gerberträger: a = 5, z = 4, t = 3 ⇒ n=0

Rechenbeispiel: (ebener) Starrkörper-Gerberträger

${\displaystyle n=5+4-3\cdot 3=0}$       ⇐       der Gerberträger ist ein statisch bestimmtes Tragwerk.

a = 5, z = 4, t = 3 ⇒ n=0 ist aber statisch überbestimmt als auch statisch unterbestimmt.

Das Abzählkriterium ist zwar eine notwendige, aber nicht hinreichende Bedingung. Unter- und Überbestimmtheiten können sich bei diesem Verfahren gegenseitig aufheben. Beispiel hierfür ist ein zweiteiliger Balken, der auf drei Loslagern liegt: Trotz ermitteltem n = 0 ist er offensichtlich nicht statisch bestimmt.^[23][20] Daher ist zusätzlich z. B. mit der Kinematik durch einen Polplan eine Aussage über die Verschieblichkeit des Tragwerks zu treffen.

Abzählkriterium für ebene Fachwerke

Ein ebenes Fachwerk:
k = 5, a = 4, s = 6

Für ebene ideale Fachwerke kann ein vereinfachtes Abzählkriterium verwendet werden, da alle Stäbe beidseitig gelenkig verbunden sind:^[24][20]

${\displaystyle n=a+s-2k}$

Hierbei sind:

${\displaystyle a}$: Summe der in den Auflagerdrehgelenken unterbundenen Bewegungsmöglichkeiten (Wertigkeiten der Auflager)

${\displaystyle s}$: Anzahl der Stäbe

${\displaystyle k}$: Anzahl der Drehgelenksknoten (Auflager + Verbindungen).

Dieses Abzählkriterium ergibt sich daraus, dass bei Fachwerken in den Auflagern und Verbindungen nur Drehgelenke vorkommen (oder als solche bewertet werden).

Beispiel: nebenstehend abgebildetes Fachwerk

${\displaystyle n=4+6-2\cdot 5=0}$       ⇐       das nebenstehend abgebildete Fachwerk ist statisch bestimmt.

Auch das Abzählkriterium für Fachwerke ist nur eine notwendige, aber nicht hinreichende Bedingung für den Nachweis statischer Bestimmtheit.^[25]

Gleichgewichtsbedingungen

Alle statisch bestimmten Systeme können mit den Gleichgewichtsbedingungen, auch Äquivalenzbedingungen, berechnet werden.

Ebenes System

Statisch bestimmtes System in der Ebene: Balken mit Festlager (links) und Loslager (rechts)

In einem starren ebenen System ist der Freiheitsgrad = 3: Zwei translatorische Bewegungsmöglichkeiten und eine rotatorische Bewegungsmöglichkeit. Um ein bestimmtes Gleichungssystem zu erhalten, sind daher drei Gleichungen nötig. Jede dieser drei Gleichungen behandelt eine Bewegungsmöglichkeit. Die Summen der Horizontalkräfte, Vertikalkräfte und Momente für einen festgelegten Bezugspunkt A müssen bei einem Gleichgewichtssystem 0 sein:

${\displaystyle \sum {F_{H}=0},\;\sum {F_{V}=0},\;\sum {M_{A}=0}}$

Der Äquivalenzsatz für allgemeine Kräftesysteme, der auf die Reduktion auf Dynamen beruht, besagt, dass bei den Gleichgewichtsbedingungen Kräftegleichungen durch Momentengleichungen ersetzt werden dürfen. Mögliche Gleichgewichtsbedingungen in der Ebene sind damit auch:

${\displaystyle \sum {F_{H}=0},\;\sum {M_{A}=0},\;\sum {M_{B}=0}}$

${\displaystyle \sum {F_{V}=0},\;\sum {M_{A}=0},\;\sum {M_{B}=0}}$

${\displaystyle \sum {M_{A}=0},\;\sum {M_{B}=0},\;\sum {M_{C}=0}}$

Bei dieser Vorgehensweise muss jedoch auf möglicherweise auftretende lineare Abhängigkeiten geachtet werden. Werden beispielsweise nur Momentengleichungen verwendet und liegen alle Bezugspunkte auf einer Geraden, so liegt keine gültige Äquivalenzbedingung vor.^[20]

In einem zentralen Kräftesystem, also einem Kräftesystem, in dem sich die Wirkungslinien aller Kräfte in einem Punkt schneiden, treten keine Momente auf, sodass hier nur zwei Gleichungen nötig sind:

${\displaystyle \sum {F_{H}=0},\;\sum {F_{V}=0}}$^[20]

Räumliches System

Im Raum gibt es drei translatorische und drei rotatorische Bewegungsmöglichkeiten, somit besteht die Gleichgewichtsbedingung aus sechs Gleichungen: Drei Gleichungen behandeln die Kraft in jeder der drei Koordinatenrichtungen, drei weitere Gleichungen das Moment in jeder der drei Koordinatenrichtungen:

${\displaystyle \sum {F_{X}=0},\;\sum {F_{Y}=0},\;\sum {F_{Z}=0},\;\sum {M_{AX}=0},\;\sum {M_{AY}=0},\;\sum {M_{AZ}=0}}$

Auch im Raum ist es möglich, eine oder mehrere Kräftegleichungen durch Momentengleichungen zu ersetzen.

Schnittgrößen infolge Zwang

In statisch bestimmten Systemen verursachen Verformungen durch Verschiebungen und Verdrehungen der Lager, Temperaturdehnungen, Kriechen und Schwinden von Beton i. A. keine Schnittgrößen, jedoch können Eigenspannungen auftreten. Durch Verformungen können z. B. Schiefstellung von Stützen hervorgerufen werden, was i. d. R. zu einer Änderung der Schnittgroßen führt.

Vor allem im Verbundbau dürfen Eigenspannungen infolge Verformungen i. A. selbst bei statisch bestimmten Systemen nicht vernachlässigt werden, man spricht dann von primären Zwängsspannungen, welche (ohne äußere Belastung) bei statisch überbestimmten Systemen zu sekundären Zwängsspannungen führen.

In statisch unbestimmten Systemen entstehen durch die o. g. Einwirkungen i. A. Schnittgrößen.

Bei der Berechnung statischer (bzw. dynamischer) Systeme sind Zwängsspannungen i. A. zu berücksichtigen.

Innere und äußere statische Bestimmtheit

Bei einer Reihe von Stabtragwerken ist es zweckmäßig und anschaulich, zwischen innerer und äußerer statischer Bestimmtheit zu unterscheiden:

• ein System heißt innerlich statisch bestimmt, falls die Schnittgrößen an geschnittenen Teilsystemen mit Hilfe der Gleichgewichtsbedingungen aus der Belastung berechnet werden können;
• ein System oder Systemteil heißt äußerlich statisch bestimmt, wenn die äußeren Lagerreaktionen allein mit Hilfe der Gleichgewichtsbedingungen aus der Belastung berechnet werden können.

Vergleich mit der mathematischen Definition

Die Definition der Bestimmung leitet sich aus dem mathematischen Begriff überbestimmt ab. Da sich jedoch sowohl manche statisch unterbestimmten wie auch manche statisch überbestimmten Systeme eindeutig lösen lassen und dabei keine der beschreibenden Gleichungen wegstreichbar ist, kann die Begrifflichkeit nicht 1:1 übertragen werden.

Wenn ein System statisch überbestimmt ist, gibt es zu viele Verformungsgleichungen (Rand- und Übergangsbedingungen), aber gleichzeitig treten zu wenig Unbekannte in den Gleichgewichtsbedingungen auf. Für die Bestimmung eindeutiger Lösungen können Beschreibungen des Verformungsverhaltens hinzugezogen werden.

Ist ein System statisch unterbestimmt, gibt es zu wenige Lagegleichungen um die Unbekannten in den Gleichgewichtsbedingungen eindeutig zu bestimmen. Zusätzliche Gleichungen, die etwa die Trägheitskräfte bei Bewegung des Systems beschreiben, können zu eindeutigen Lösungen führen.

Beispiele

Der Einfeldträger wird häufig als Grundbeispiel für ein statisches System angeführt

Ein Dreigelenkbogen

Statisch bestimmte Systeme sind zum Beispiel:

• Einfeldträger (Träger auf zwei Stützen)
  • Einfeldträger mit Kragarm
• Kragträger
• Dreigelenkrahmen
• Dreigelenkbogen
• Gerberträger

Statisch unbestimmte Systeme sind zum Beispiel:

• Durchlaufträger

Beispiele für ein äußerlich bestimmtes, aber innerlich unbestimmtes System:

• Rahmenfachwerkträger.

Literatur

• N. Hinrichs: Keine Panik vor Mechanik! Springer, 2009, ISBN 978-3-8348-0646-8 (eingeschränkte Vorschau in der Google-Buchsuche).
• C. Spura: Technische Mechanik 1. Stereostatik. Springer, 2016, ISBN 978-3-658-14984-0.
• Karl-Eugen Kurrer: Geschichte der Baustatik. Auf der Suche nach dem Gleichgewicht, Ernst und Sohn, Berlin 2016, ISBN 978-3-433-03134-6, S. 32 ff.

Anmerkungen