Sekans und Kosekans

Sekans und Kosekans sind trigonometrische Funktionen. Der Sekans wird mit ${\displaystyle \sec(x)}$ bezeichnet, der Kosekans mit ${\displaystyle \csc(x)}$ oder ${\displaystyle \operatorname {cosec} (x)}$^[1]. Die Funktionen haben ihren Namen durch die Definition im Einheitskreis. Die Funktionswerte entsprechen der Länge von Sekantenabschnitten:

${\displaystyle {\overline {OT}}=\sec(b)\qquad \qquad {\overline {OK}}=\csc(b)}$

Ein rechtwinkliges Dreieck

Definitionen am Einheitskreis
${\displaystyle {\overline {OT}}=\sec b\$ ;\ {\overline {OK}}=\csc b}

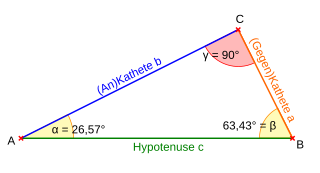
Im rechtwinkligen Dreieck ist der Sekans das Verhältnis der Hypotenuse zur Ankathete und damit die Kehrwert-Funktion der Kosinusfunktion.

Der Kosekans ist das Verhältnis der Hypotenuse zur Gegenkathete und damit die Kehrwert-Funktion der Sinusfunktion:

${\displaystyle {\begin{aligned}\sec(\alpha )&={\frac {l_{\text{Hy}}}{l_{\text{AK}}}}={\frac {c}{b}}\quad &\quad \csc(\alpha )&={\frac {l_{\text{Hy}}}{l_{\text{GK}}}}={\frac {c}{a}}\\\sec(x)&={\frac {1}{\cos(x)}}\quad &\quad \csc(x)&={\frac {1}{\sin(x)}}\end{aligned}}}$

Eigenschaften

Graphen

Graph der Sekansfunktion

Graph der Kosekansfunktion

Definitionsbereich

Sekans:	${\displaystyle -\infty <x<+\infty \quad$ ;\quad x\neq \left(n+{\frac {1}{2}}\right)\cdot \pi \,;\,n\in \mathbb {Z} }
Kosekans:	${\displaystyle -\infty <x<+\infty \quad$ ;\quad x\neq n\cdot \pi \ ;\,n\in \mathbb {Z} }

Wertebereich

${\displaystyle -\infty <f(x)\leq -1\quad$ ;\quad 1\leq f(x)<+\infty }

Periodizität

Periodenlänge ${\displaystyle 2\cdot \pi \,:\,f(x+2\pi )=f(x)}$

Symmetrien

Sekans:	Achsensymmetrie: ${\displaystyle f(x)=f(-x)}$
Kosekans:	Punktsymmetrie: ${\displaystyle f(-x)=-f(x)}$

Polstellen

Sekans:	${\displaystyle x=\left(n+{\frac {1}{2}}\right)\cdot \pi \,;\,n\in \mathbb {Z} }$
Kosekans:	${\displaystyle x=n\cdot \pi \$ ;\quad n\in \mathbb {Z} }

Extremstellen

Sekans:	Minima:	${\displaystyle x=2n\cdot \pi \,;\,n\in \mathbb {Z} }$	Maxima:	${\displaystyle x=(2n-1)\cdot \pi \$ ;\,n\in \mathbb {Z} }
Kosekans:	Minima:	${\displaystyle x=\left(2n+{\frac {1}{2}}\right)\cdot \pi \$ ;\,n\in \mathbb {Z} }	Maxima:	${\displaystyle x=\left(2n-{\frac {1}{2}}\right)\cdot \pi \$ ;\,n\in \mathbb {Z} }

Nullstellen

Beide Funktionen haben keine Nullstellen.

Asymptoten

Beide Funktionen haben keine horizontalen Asymptoten.

Sprungstellen

Beide Funktionen haben Sprungstellen.

Wendepunkte

Beide Funktionen haben keine Wendepunkte.

Wichtige Funktionswerte

Da Sekans und Kosekans periodische Funktionen mit der Periode ${\displaystyle 2\pi }$ (entspricht im Gradmaß ${\displaystyle 360^{\circ }}$) sind, reicht es, die Funktionswerte des Sekans für den Bereich ${\displaystyle 0\leq x\leq 2\pi \,;\quad x\neq {\frac {\pi }{2}},x\neq {\frac {3\pi }{2}}}$ und die des Kosekans für den Bereich ${\displaystyle 0\leq x\leq 2\pi \,;\quad x\neq 0,x\neq \pi ,x\neq 2\pi }$ zu kennen. Funktionswerte außerhalb dieses Bereichs können also aufgrund der Periodizität durch den Zusammenhang

${\displaystyle \sec(x)=\sec(x+2k\pi )\quad {\text{und}}\quad \csc(x)=\csc(x+2k\pi )}$

bestimmt werden. In Gradmaß lautet der Zusammenhang analog

${\displaystyle \sec(x)=\sec(x+k\cdot 360^{\circ })\quad {\text{und}}\quad \csc(x)=\csc(x+k\cdot 360^{\circ })\,.}$

Hierbei bezeichnet ${\displaystyle k\in \mathbb {Z} }$ eine ganze Zahl. Die folgende Tabelle listet die wichtigen Funktionswerte der beiden trigonometrischen Funktionen in einer leicht zu merkenden Reihe auf.^[2]

Winkel (Grad)	Bogenmaß	Sekans	Kosekans
${\displaystyle 0^{\circ }}$	${\displaystyle 0}$	${\displaystyle {\frac {2}{\sqrt {4}}}=1}$	${\displaystyle -}$
${\displaystyle 30^{\circ }}$	${\displaystyle {\frac {\pi }{6}}}$	${\displaystyle {\frac {2}{\sqrt {3}}}={\frac {2}{3}}{\sqrt {3}}}$	${\displaystyle {\frac {2}{\sqrt {1}}}=2}$
${\displaystyle 45^{\circ }}$	${\displaystyle {\frac {\pi }{4}}}$	${\displaystyle {\frac {2}{\sqrt {2}}}={\sqrt {2}}}$	${\displaystyle {\frac {2}{\sqrt {2}}}={\sqrt {2}}}$
${\displaystyle 60^{\circ }}$	${\displaystyle {\frac {\pi }{3}}}$	${\displaystyle {\frac {2}{\sqrt {1}}}=2}$	${\displaystyle {\frac {2}{\sqrt {3}}}={\frac {2}{3}}{\sqrt {3}}}$
${\displaystyle 90^{\circ }}$	${\displaystyle {\frac {\pi }{2}}}$	${\displaystyle -}$	${\displaystyle {\frac {1}{2}}{\sqrt {4}}=1}$

Weitere wichtige Werte sind:

Winkel (Grad)	Bogenmaß	Sekans	Kosekans
${\displaystyle 15^{\circ }}$	${\displaystyle {\tfrac {\pi }{12}}}$	${\displaystyle {\sqrt {6}}-{\sqrt {2}}}$	${\displaystyle {\sqrt {6}}+{\sqrt {2}}}$
${\displaystyle 18^{\circ }}$	${\displaystyle {\tfrac {\pi }{10}}}$	${\displaystyle {\tfrac {1}{5}}{\sqrt {50-10{\sqrt {5}}}}}$	${\displaystyle 1+{\sqrt {5}}}$
${\displaystyle 36^{\circ }}$	${\displaystyle {\tfrac {\pi }{5}}}$	${\displaystyle {\sqrt {5}}-1}$	${\displaystyle {\tfrac {1}{5}}{\sqrt {50+10{\sqrt {5}}}}}$
${\displaystyle 54^{\circ }}$	${\displaystyle {\tfrac {3\pi }{10}}}$	${\displaystyle {\tfrac {1}{5}}{\sqrt {50+10{\sqrt {5}}}}}$	${\displaystyle {\sqrt {5}}-1}$
${\displaystyle 72^{\circ }}$	${\displaystyle {\tfrac {2\pi }{5}}}$	${\displaystyle 1+{\sqrt {5}}}$	${\displaystyle {\tfrac {1}{5}}{\sqrt {50-10{\sqrt {5}}}}}$
${\displaystyle 75^{\circ }}$	${\displaystyle {\tfrac {5\pi }{12}}}$	${\displaystyle {\sqrt {6}}+{\sqrt {2}}}$	${\displaystyle {\sqrt {6}}-{\sqrt {2}}}$
${\displaystyle 180^{\circ }}$	${\displaystyle \pi }$	${\displaystyle -1}$	${\displaystyle -}$
${\displaystyle 270^{\circ }}$	${\displaystyle {\frac {3\pi }{2}}}$	${\displaystyle -}$	${\displaystyle -1}$
${\displaystyle 360^{\circ }}$	${\displaystyle 2\pi }$	${\displaystyle 1}$	${\displaystyle -}$

Beweisskizzen:

• ${\displaystyle \sec(45^{\circ })=\csc(45^{\circ })={\sqrt {2}}}$, weil das rechtwinklige Dreieck im Einheitskreis (mit der Hypotenuse 1) dann gleichschenklig ist, und nach Pythagoras gilt ${\displaystyle 1^{2}+1^{2}=x^{2}\Rightarrow x={\sqrt {2}}}$.
• ${\displaystyle \sec(60^{\circ })=\csc(30^{\circ })=2}$, weil das rechtwinklige Dreieck im Einheitskreis (mit der Hypotenuse 1) gespiegelt an der ${\displaystyle x}$-Achse dann gleichseitig ist (mit Seitenlänge 1), und somit die Seitenlänge die doppelte Länge der Gegenkathete ist.
• ${\displaystyle \sec(30^{\circ })=\csc(60^{\circ })={\tfrac {2}{3}}{\sqrt {3}}}$, weil für das rechtwinklige Dreieck im Einheitskreis (mit der Hypotenuse 1) wegen ${\displaystyle \sin(30^{\circ })={\tfrac {1}{2}}}$ für den Sekans nach Pythagoras gilt ${\displaystyle ({\tfrac {1}{x}})^{2}+\left({\tfrac {1}{2}}\right)^{2}=1^{2}\ \Rightarrow \ {\tfrac {1}{x^{2}}}={\tfrac {3}{4}}\ \Rightarrow \ x^{2}={\tfrac {4}{3}}\ \Rightarrow \ x={\tfrac {2}{3}}{\sqrt {3}}}$.
• ${\displaystyle \sec(72^{\circ })=\csc(18^{\circ })={\frac {1}{{\tfrac {1}{4}}({\sqrt {5}}-1)}}=1+{\sqrt {5}}}$, weil im Pentagramm das Inverse des Goldenen Schnitts auftritt, wobei der halbierte Winkel in den Spitzen gleich 18° ist.
• ${\displaystyle \sec(36^{\circ })=\csc(54^{\circ })={\frac {1}{{\tfrac {1}{4}}(1+{\sqrt {5}})}}={\sqrt {5}}-1}$, weil im regelmäßigen Fünfeck der Goldene Schnitt auftritt, wobei der halbierte Innenwinkel gleich 54° ist.
• ${\displaystyle \sec(75^{\circ })=\csc(15^{\circ })}$ und ${\displaystyle \sec(15^{\circ })=\csc(75^{\circ })}$ lassen sich mit Hilfe der Halbwinkelformeln für Sinus und Kosinus herleiten.

Weitere mit Quadratwurzeln darstellbare Funktionswerte

Siehe auch: Sinus und Kosinus: Weitere mit Quadratwurzeln angebbare Funktionswerte

Weil der Sekans jeweils der Kehrwert des Kosinus und der Kosekans der Kehrwert des Sinus ist, lassen sich die Funktionswerte ${\displaystyle \csc(x)}$ und ${\displaystyle \sec(x)}$ genau dann mit Quadratwurzeln darstellen, wenn das auch für ${\displaystyle \sin(x)}$ und ${\displaystyle \cos(x)}$ möglich ist. Generell gilt, dass ${\displaystyle \csc \alpha \;}$ und ${\displaystyle \sec \alpha \;}$ genau dann explizit mit den vier Grundrechenarten und Quadratwurzeln darstellbar sind, wenn der Winkel ${\displaystyle \alpha \;}$ mit Zirkel und Lineal konstruierbar ist, insbesondere also wenn ${\displaystyle \alpha \;}$ von der Gestalt

${\displaystyle \alpha =k{\frac {360^{\circ }}{2^{n}p_{1}\dots p_{r}}}}$

ist, wobei ${\displaystyle k\in \mathbb {Z} \;}$, ${\displaystyle n\in \mathbb {N} _{0}\;}$ und die ${\displaystyle p_{i}\;}$ für ${\displaystyle i=1,\dots ,r\;}$ Fermatsche Primzahlen sind.^[3]

Umkehrfunktionen

Sekans:

Auf einer halben Periodenlänge, z. B. ${\displaystyle x\in [0,\pi ]}$ ist die Funktion umkehrbar (Arkussekans):

${\displaystyle x=\operatorname {arcsec}(y)}$

Kosekans

Auf einer halben Periodenlänge, z. B. ${\displaystyle x\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}$ ist die Funktion umkehrbar (Arkuskosekans):

${\displaystyle x=\operatorname {arccsc}(y)}$

Reihenentwicklung

Summenreihen

Sekans:

${\displaystyle \sec(x)=4\pi \,\sum _{k=0}^{\infty }{\frac {(-1)^{k}(2k+1)}{(2k+1)^{2}\pi ^{2}-4x^{2}}}}$

Kosekans:

${\displaystyle \csc(x)={\frac {1}{x}}-2x\,\sum _{k=1}^{\infty }{\frac {(-1)^{k}}{k^{2}\pi ^{2}-x^{2}}}=\sum _{k=-\infty }^{\infty }{\frac {(-1)^{k}\,x}{x^{2}-k^{2}\pi ^{2}}}}$

Fakultät und Produktreihe

Mit Hilfe der Fakultätsfunktion beziehungsweise der Gaußschen Pifunktion können Sekans und Kosekans wie folgt dargestellt werden:

Sekans:

${\displaystyle \sec(\pi \,x)={\frac {4\,\Pi ({\tfrac {1}{2}}-x)\,\Pi ({\tfrac {1}{2}}+x)}{\pi \,(1-2\,x)\,(1+2\,x)}}}$

Kosekans:

${\displaystyle \csc(\pi \,x)={\frac {\Pi (x)\,\Pi (1-x)}{\pi \,x\,(1-x)}}}$

Die Fakultätsfunktion entspricht der Eulerschen Gammafunktion von der Nachfolgerfunktion und kann demnach für alle reellen Zahlen ${\displaystyle x\in \mathbb {R} }$ so definiert werden:

${\displaystyle x!=\Pi (x)=\Gamma (x+1)=\exp(-\,\gamma \,x)\prod _{n=1}^{\infty }\left[\left(1+{\frac {x}{n}}\right)^{-1}\exp \left({\frac {x}{n}}\right)\right]}$

Die nun gezeigte Produktreihe wird Weierstraßsches Produkt genannt und dient der Ermittlung von Sekans und Kosekans mittels Produktentwicklungen.

Mit dem griechischen Buchstaben ${\displaystyle \gamma }$ wird die Euler-Mascheroni-Konstante dargestellt.

Ableitung

Sekans:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\sec(x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {1} }{\cos(x)}}={\frac {+\sin(x)}{\cos ^{2}(x)}}=+\sec(x)\cdot \tan(x)=+{\frac {\sec ^{2}(x)}{\csc(x)}}}$

Kosekans

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\csc(x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {1} }{\sin(x)}}={\frac {-\cos(x)}{\sin ^{2}(x)}}=-\csc(x)\cdot \cot(x)=-{\frac {\csc ^{2}(x)}{\sec(x)}}}$

Integral

Sekans:

${\displaystyle \int \sec(x)\,\mathrm {d} x=\ln \left|{\frac {1+\sin(x)}{\cos(x)}}\right|+C=\ln {\Big |}\sec(x)+\tan(x){\Big |}+C=\ln \left|\tan \left({\frac {x}{2}}+{\frac {\pi }{4}}\right)\right|+C={\frac {1}{2}}\ln \left({\frac {1+\sin x}{1-\sin x}}\right)+C}$

Kosekans

${\displaystyle \int \csc(x)\,\mathrm {d} x=\ln \left|{\frac {\sin(x)}{1+\cos(x)}}\right|+C=\ln \left|\tan \left({\frac {x}{2}}\right)\right|+C}$

Komplexes Argument

${\displaystyle \sec(x+\mathrm {i} \!\cdot \!y)={\frac {2\cos(x)\cosh(y)}{\cos(2x)+\cosh(2y)}}+\mathrm {i} \;{\frac {2\sin(x)\sinh(y)}{\cos(2x)+\cosh(2y)}}}$   mit ${\displaystyle x,y\in \mathbb {R} }$

${\displaystyle \csc(x+\mathrm {i} \!\cdot \!y)={\frac {-2\sin(x)\cosh(y)}{\cos(2x)-\cosh(2y)}}+\mathrm {i} \;{\frac {2\cos(x)\sinh(y)}{\cos(2x)-\cosh(2y)}}}$   mit ${\displaystyle x,y\in \mathbb {R} }$

Anwendung für numerische Berechnungen – Bedeutung historisch

Bevor elektronische Rechenmaschinen allgegenwärtig waren, verwendete man für die Winkelfunktionen Tabellen, meist in gedruckten Büchern. Mit einem solchen Funktionswert aus einer Tabelle zu multiplizieren war bequemer und praktischer, als durch so einen Wert zu dividieren (dies gilt übrigens auch für nicht aufgehende Wurzelwerte usw.); wenn in einer Formel also ein Sinus oder Kosinus im Nenner steht, ist es bequem, statt dieser Werte die entsprechenden Kosekans- bzw. Sekanswerte in den Zähler zu schreiben.

Dieses Argument ist im Zeitalter der allgemein verfügbaren elektronischen Taschenrechner nur noch von historischer Bedeutung; Sekans und Kosekans sind in den neueren Formelsammlungen nicht mehr erwähnt und auch nicht als Funktionen (mit eigener Taste) in den Rechnern implementiert. Für diesen Zweck sind diese Funktionen schlicht überflüssig geworden; sie lösten ein Problem, das nicht mehr besteht.

Siehe auch

• Sinus und Kosinus
• Tangens und Kotangens
• Trigonometrische Funktion
• Sekans hyperbolicus und Kosekans hyperbolicus
• Formelsammlung Trigonometrie

Weblinks

• Eric W. Weisstein: Secant und Cosecant auf MathWorld

Einzelnachweise

1. Konstantin A. Semendjajew: Taschenbuch der Mathematik. Verlag Harri Deutsch, 2008, ISBN 3-8171-2007-9, S. 1220 (eingeschränkte Vorschau in der Google-Buchsuche).
2. Georg Hoever: Höhere Mathematik kompakt. Springer Spektrum, Berlin Heidelberg 2014, ISBN 978-3-662-43994-4 (eingeschränkte Vorschau in der Google-Buchsuche).
3. Emil Artin: Galoissche Theorie. Verlag Harri Deutsch, Zürich 1973, ISBN 3-87144-167-8, S. 85.

Trigonometrische Funktion

Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und Kosekans 

Umkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und Arkuskosekans 

Hyperbelfunktionen
Sinus hyperbolicus und Kosinus hyperbolicus | Tangens hyperbolicus und Kotangens hyperbolicus | Sekans hyperbolicus und Kosekans hyperbolicus 

Areafunktionen
Areasinus hyperbolicus und Areakosinus hyperbolicus | Areatangens hyperbolicus und Areakotangens hyperbolicus | Areasekans hyperbolicus und Areakosekans hyperbolicus