quocient de la velocitat de la llum en el buit entre la velocitat de la llum en el medi en qüestió From Wikipedia, the free encyclopedia
En òptica, l'índex refractiu o índex de refracció n d'un material és un nombre adimensional que descriu com es propaga la llum a través d'aquest mitjà. Es defineix com

on c és la velocitat de la llum en el buit i v és la velocitat de fase de la llum en el medi. Per exemple, l'índex de refracció de l'aigua és 1,333, el que significa que la llum viatja a 1,333 vegades més ràpid en un buit del que ho faria en l'aigua.

L'índex de refracció determina com es corba la llum, o refracta, en entrar en un material. Aquest és el primer ús documentat de l'índex de refracció i va ser descrit per la llei de Snell de refracció, n1 sinθ1 = n₂ sinθ₂, on θ1 i θ₂ són els angles d'incidència i refracció, respectivament, d'un raig que travessa la interfície entre dos mitjans amb índexs de refracció n1 i n₂.
Els índexs de refracció també determinen la quantitat de llum que es reflecteix en arribar a la interfície, així com l'angle crític per a la reflexió interna total i l'angle de Brewster.[1]
L'índex de refracció pot ser vist com el factor pel qual la velocitat i la longitud d'ona de la radiació es redueixen respecte als seus valors de buit: la velocitat de la llum en un medi és v = c / n, i de manera similar la longitud d'ona en aquest mitjà és λ = λ0 / n, on λ0 és la longitud d'ona de la llum en el buit. Això implica que en el buit té un índex de refracció d'1, i que la freqüència (f = v / λ) de l'ona no es veu afectada per l'índex de refracció.
L'índex de refracció varia amb la longitud d'ona de la llum. Això es coneix com a dispersió òptica i fa que la llum blanca es divideixi en seus colors constituents en prismes, formant l'arc de Sant Martí, i l'aberració cromàtica en les lents. En la propagació de la llum en els materials absorbents es pot descriure l'ús d'un índex de refracció de valor complex.[2] La part imaginària llavors representa l'atenuació, mentre que la part real representa la refracció.
El concepte d'índex de refracció és àmpliament utilitzat en tot l'espectre electromagnètic, des dels raigs X fins a les ones de ràdio. En general, es defineix l'índex de refracció a partir de la teoria electromagnètica com l'arrel quadrada del producte de la constant dielèctrica () i la permeabilitat magnètica () del material:
També es pot utilitzar amb els fenòmens d'ones, com el so. En aquest cas la velocitat del so s'utilitza en lloc de la velocitat de la llum i el mitjà de referència elegit ha de ser diferent del buit.[3]
L'índex de refracció n d'un medi òptic es defineix com la relació de la velocitat de la llum en el buit, c = 299.792.458 m/s, i la velocitat de fase v de la llum en el medi,[1]
La velocitat de fase és la velocitat a la qual la fase de l'ona (o cresta) es mou, i que pot ser diferent de la velocitat de grup, la velocitat a la qual el pols de llum o l'envolvent de l'ona es mou.
La definició anterior es refereix de vegades com l'índex refractiu absolut o l'índex absolut de refracció per distingir-ho de les definicions on la velocitat de la llum s'ha utilitzat en altres mitjans de referència diferents al buit.[1] Històricament, s'ha utilitzat l'aire a una pressió i temperatura estàndard com a mitjà de referència.

Probablement, Thomas Young va ser la persona que va inventar i utilitzar per primera vegada el terme «índex de refracció», en 1807.[4] Al mateix temps, ell va escriure en un sol nombre aquest valor de en lloc de fer-lo com una relació de dos nombres com es feia habitualment.
Newton, que la va anomenar «proporció dels sinus d'incidència i refracció», la va escriure com un quocient de dos nombres (com 529 a 396, o gairebé 4 a 3, per a l'aigua).[5]
Hauksbee, que la va anomenar «relació de refracció», la va escriure com una relació amb un numerador fix (com 10000 a 7451,9 per a l'orina).[6]
Hutton la va escriure com una relació amb un denominador fix (com 1,3358 a 1 per l'aigua).[7]
Young no va utilitzar símbols per a l'índex de refracció en 1807. En els propers anys, altres van començar a utilitzar diferents símbols: n, m i μ.[8][9][10] El símbol n va prevaler gradualment.

| Material | n |
|---|---|
| Buit | 1 |
| Gassos a 0 °C i 1 atm | |
| Aire | 1,000293 |
| Heli | 1,000036 |
| Hidrògen | 1,000132 |
| Diòxid de carboni | 1,00045 |
| Líquids a 20 °C | |
| Aigua | 1,333 |
| Etanol | 1,36 |
| Oli d'oliva | 1,47 |
| Sòlids | |
| Gel | 1,31 |
| Vidre comú | 1,46 |
| PMMA | 1,49 |
| Vidre crown | 1,52 |
| Vidre flint | 1,62 |
| Zircònia cúbica | 2,15 |
| Diamant | 2,42 |
| Moissanita | 2,65 |
| Selenur de zinc | 2,67 |
Per a la llum visible, els objectes més transparents tenen índexs de refracció entre 1 i 2. Alguns exemples es donen a la taula adjacent. Aquests valors es mesuren en el «doblet del sodi», la línia D de sodi, amb una longitud d'ona de 589 nanòmetres, com es fa convencionalment.
Els gasos a pressió atmosfèrica tenen índexs de refracció propers a 1, per la seva baixa densitat. Gairebé tots els sòlids i els líquids tenen índexs de refracció per sobre de 1,3, amb l'excepció clara de l'aerogel. L'aerogel és sòlid de molt baixa densitat que té un índex de refracció en l'interval entre 1,002 i 1,265.[11]
La moissanita es troba a l'altre extrem de la gamma amb un índex de refracció tan alt com 2,65. La majoria dels plàstics tenen índexs de refracció entre els rangs 1,3 i 1,7, però alguns polímers d'alt índex de refracció poden tenir valors de fins a 1,76.[12]
Per a la llum infraroja, els índexs de refracció poden ser considerablement més grans. El germani és transparent a la regió de longitud d'ona de 2 a 14 micres i té un índex de refracció d'aproximadament 4, i per això és un material important per a l'òptica d'infraroigs.[13]
D'acord amb la teoria de la relativitat, cap informació pot viatjar més ràpid que la velocitat de la llum en el buit, però això no vol dir que l'índex de refracció no pot ser inferior a 1. L'índex de refracció es mesura en la velocitat de fase de la llum, que no porta informació.[Nota 1]
La velocitat de fase és la velocitat a la qual les crestes de l'ona es mouen i poden ser més ràpides que la velocitat de la llum en el buit, i això pot donar un índex de refracció per sota d' 1. Això pot ocórrer prop de les freqüències de ressonància, per l'absorció del medi, en els plasmes, i en les radiografies. En el règim dels raigs X, els índexs de refracció són inferiors però molt a prop d'1 (a excepcions d'algunes freqüències de ressonància).[15]
Com a exemple, l'aigua té un índex de refracció de 0,99999974 (1 − 2,6×10−7) per a la radiació de raigs X a una energia de fotó de 30 keV (0,04 nm longitud d'ona).[15]
La investigació recent ha demostrat també l'existència de materials amb un índex de refracció negatiu, que pot passar si la permitivitat i la permeabilitat tenen valors negatius simultanis.[16] Això es pot aconseguir amb els metamaterials de construcció periòdica. La refracció negativa resultant (és a dir, una inversió de la llei de Snell) ofereix la possibilitat dels superlents i altres fenòmens exòtics.[17]
A la microescala, la velocitat de fase d'una ona electromagnètica es fa més lenta en un material a causa que el camp elèctric crea una pertorbació en les càrregues de cada àtom (principalment els electrons) proporcional a la susceptibilitat elèctrica del medi (de la mateixa manera, el camp magnètic crea una pertorbació de la susceptibilitat magnètica). A mesura que els camps electromagnètics oscil·len en l'ona, les càrregues en el material seran «sacsejades» d'anada i tornada a la mateixa freqüència.[18]Així, les càrregues irradien la seva pròpia ona electromagnètica que es troba en la mateixa freqüència, però en general amb un retard de fase, ja que les càrregues es poden moure fora de fase amb la força d'accionament (vegeu oscil·lador harmònic sinusoidal conduït).
L'ona de la llum que viatja en el medi és la superposició macroscòpica (suma) de totes aquestes contribucions en la matèria: l'ona original, a més de les ones radiades per totes les càrregues en moviment. Aquesta ona és típicament una ona amb la mateixa freqüència però de longitud d'ona més curta que l'original, que porta a un alentiment de la velocitat de fase de l'ona. La major part de la radiació de l'oscil·lació del material de les càrregues modifiquen l'ona d'entrada, canviant la seva velocitat. No obstant això, una mica d'energia neta serà radiada en altres direccions, o fins i tot a altres freqüències (vegeu dispersió).
Depenent de la fase relativa de l'ona de conducció original i les ones radiades pel moviment de càrrega, hi ha diverses possibilitats:
Per a la majoria dels materials a freqüències de llum visible, la fase és entre 90° i 180°, que correspon a una combinació de la refracció i l'absorció.

L'índex de refracció dels materials varia amb la longitud d'ona (i freqüència) de la llum.[20] Això es coneix com a dispersió i fa que els prismes divideixin la llum blanca en els seus colors espectrals constituents.[21] Com l'índex de refracció varia amb la longitud d'ona, també ho farà l'angle de refracció quan la llum passa d'un material a un altre. La dispersió també fa que la distància focal de les lents depenen de la longitud d'ona. Aquest és un tipus d'aberració cromàtica que sovint s'ha de corregir en sistemes d'imatges.
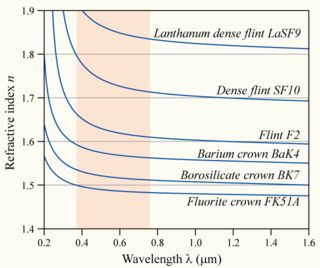
En les regions de l'espectre on el material no absorbeix la llum, l'índex de refracció tendeix a disminuir amb l'augment de longitud d'ona, i per tant augmentar amb la freqüència. Això es coneix com a «dispersió normal», en contrast amb la «dispersió anòmala», on l'índex de refracció augmenta amb la longitud d'ona.[20] Per a la dispersió normal de la llum visible, significa que l'índex de refracció és més gran per a la llum blava que per a la vermella.
Per l'òptica en el rang visual, la quantitat de dispersió d'un material de la lent sovint es quantifica pel nombre d'Abbe:[21]
Per a una descripció més precisa de la dependència de longitud d'ona de l'índex de refracció, es pot utilitzar l'equació de Sellmeier.[22] És una fórmula empírica que funciona bé en la descripció de la dispersió. Sovint, els coeficients de Sellmeier són citats en les taules en lloc de l'índex de refracció.
A causa de la dispersió, en general és important especificar la longitud d'ona de buit de la llum per a la qual es mesura un índex de refracció. Típicament, els mesuraments es realitzen en diverses línies d'emissió espectrals ben definides; per exemple nD, en general es denota l'índex de refracció en la línia D de Fraunhofer, el centre de la doble emissió groga del sodi a 589,29 nm de longitud d'ona.
Quan la llum passa a través d'un mitjà, sempre s'atenuarà part d'ella. Això pot ser pres en compte convenientment mitjançant la definició d'un índex de refracció complex,
En aquest cas, la part real n és l'índex de refracció i indica la velocitat de fase, mentre que la part imaginària κ s'anomena coeficient d'extinció (malgrat que κ també pot referir-se al coeficient d'absorció de massa) .[23] i indica la quantitat d'absorció quan l'ona electromagnètica es propaga a través del material.[24]
Aquesta κ correspon a l'absorció que es pot veure mitjançant la inserció d'aquest índex de refracció en l'expressió del camp elèctric d'una ona electromagnètica plana que viatja en la direcció z. Podem fer això relacionant el nombre complex de l'ona k a l'índex de refracció complex n a través de k = 2πn/λ0, sent λ0 la longitud d'ona al buit; aquest pot ser inserit en l'expressió d'ona plana com
Aquí veiem que κ dona un decaïment exponencial, com s'esperava en la llei de Beer-Lambert. La intensitat és proporcional al quadrat del camp elèctric, que dependrà de la profunditat en el material que ès exp(−4πκz/λ0), i el coeficient d'absorció es converteix en α = 4πκ/λ0[1]:128 Això també es repeteix a la profunditat de penetració, la distància després de la qual cosa la intensitat es redueix en 1/e, δp = 1/α = λ0/(4πκ).

Tant n com κ depenen de la freqüència. En la majoria de les circumstàncies κ > 0 (la llum és absorbida) o κ = 0 (la llum viatja sempre sense pèrdues). En situacions especials, especialment en el medi actiu del làser, també és possible que κ < 0 (la llum s'amplifica).
Una convenció alternativa utilitza n = n − iκ en lloc de n = n + iκ, però κ > 0 encara es correspon amb la pèrdua. Per tant aquestes dues convencions són inconsistents i no s'han de confondre. La diferència està relacionada amb la definició de dependència del temps sinusoidal, que ès Re[exp(−iωt)] enfront de Re[exp(+iωt)] (vegeu descripcions matemàtiques de l'opacitat).
La pèrdua dielèctrica i la conductivitat no-zero del CC en els materials causen absorció. Els bons materials dielèctrics, com ara vidre, tenen molt baixa conductivitat CC, i en les baixes freqüències la pèrdua dielèctrica també és insignificant, fent que gairebé hagi cap absorció. No obstant això, a freqüències més altes (per exemple la llum visible), la pèrdua dielèctrica pot augmentar l'absorció de manera significativa, reduint la transparència del material en aquestes freqüències.
La real (n) i la imaginària (κ), parts de l'índex de refracció complex, es relacionen a través de les relacions de Kramers-Kronig. En 1986, A.R. Forouhi i I. Bloomer van deduir una equació que descriu κ com una funció de l'energia fotònica (E) aplicable als materials amorfs. Forouhi i Bloomer apliquen llavors la relació Kramers-Kronig per derivar l'equació corresponent per a n com a funció de la E. El mateix formalisme es va aplicar als materials cristal·lins per Forouhi i Bloomer en 1988.
L'índex de refracció i el coeficient d'extinció (n i κ) no es poden mesurar directament. S'han de determinar indirectament de quantitats mesurables que en depenen, com ara la reflectància (R) o la transmitància (T), o paràmetres elipsométriques, ψ i δ. La determinació de n i κ d'aquestes quantitats mesurades implicarà el desenvolupament d'una expressió teòrica per a R o T (o ψ i δ) en termes d'un model físic vàlid per n i κ. Ajustar el model teòric a la mesura R o T (o ψ i δ) amb anàlisi de regressió, es poden deduir n i κ .
Per als raigs X i la radiació ultraviolada extrema, l'índex de refracció complex es desvia lleugerament de la unitat i en general té una part real menor que 1. Per tant, s'escriu normalment com a n = 1 − δ + iβ (o n = 1 − δ − iβ amb la convenció alternativa esmentada anteriorment).[2]

El camí òptic (Optical Path Length, OPL) és el producte de la longitud del camí geomètric d de la llum segueix a través del sistema, i l'índex de refracció del medi a través del qual es propaga.[25]
Aquest és un concepte important en l'òptica, ja que determina la fase de la llum i administra la interferència i la difracció de la llum a mesura que es propaga. D'acord amb el principi de Fermat, els raigs de llum poden ser tan característics en aquestes corbes que optimitzen la longitud del camí òptic.[1]

Quan la llum es mou des d'un medi cap a un altre, canvia de direcció, és a dir, es refracta. Si es passa d'un medi amb índex de refracció n1 cap a un altre amb índex de refracció n₂, amb un angle d'incidència en la superfície normal de θ1, l'angle de refracció θ₂ es pot calcular a partir de la llei de Snell:[26]
Quan la llum entra d'un material amb alt índex de refracció, l'angle de refracció serà més petit que l'angle d'incidència i la llum serà refractada cap a la normal de la superfície. Com més gran és l'índex de refracció, la llum viatjarà més a prop a la direcció normal. En passar a un mitjà amb un índex de refracció més baix, la llum, en lloc es refractar-se, s'allunya de la normal, cap a la superfície.

Si no existeix un angle θ₂ que completi la llei de Snell, és a dir,
la llum no pot ser transmèsa i en el seu lloc pateix una reflexió total.[27] Això passa només quan la llum va cap a un material menys dens òpticament, és a dir, un amb menor índex de refracció.
Per aconseguir la reflexió total, l'angle d'incidència θ1 ha de ser major que l'angle crític.[28]
Part de la llum transmesa també hi ha una part que es reflecteix. L'angle de reflexió és igual a l'angle d'incidència, i la quantitat de llum que es reflecteix es determina per la reflectivitat de la superfície. La reflectivitat es pot calcular a partir de l'índex de refracció i l'angle d'incidència amb les equacions de Fresnel, que per incidència normal es redueix a:[29]
Per al vidre comú en l'aire, n1 = 1 i n ₂ = 1,5 i, per tant, al voltant del 4% de la potència incident és reflectida. Per a altres angles d'incidència, la reflectivitat també dependrà de la polarització de la llum entrant. En un cert angle, anomenat angle de Brewster, la llum p-polaritzada (llum amb el camp elèctric en el pla d'incidència) serà transmesa completament. L'angle de Brewster es pot calcular a partir dels dos índexs de refracció de la interfície[1]: 245

La distància focal d'una lent està determinada pel seu índex de refracció n i els radis de curvatura R1 i R₂ de les seves superfícies. La potència d'una lent prima en l'aire ve donada per la fórmula del fabricant de lents:[30]
on f és la longitud focal de la lent.
La resolució d'un bon microscopi òptic està determinada principalment per l'obertura numèrica (numeral aperture, NA) de la seva lent d'objectiu. L'obertura numèrica al seu torn està determinat per l'índex de refracció n del medi que omple l'espai entre la mostra i la lent, i l'angle de recollida de la llum mitjana θ d'acord amb:[31]
Per aquesta raó s'utilitza normalment oli d'immersió per a obtenir una alta resolució en el microscopi. En aquesta tècnica, l'objectiu se submergeix en una gota d'oli d'immersió d'índex de refracció alt en la mostra sota estudi.[31]
L'índex de refracció de la radiació electromagnètica és igual a
on εr és la permitivitat relativa del material, i μr és la permeabilitat relativa.[32] L'índex de refracció és utilitzada pels òptics en les equacions de Fresnel i la llei de Snell; mentre que la constant dielèctrica i la permeabilitat s'utilitzen en les equacions de Maxwell i en l'electrònica.
Molts materials d'origen natural no són magnètics a freqüències òptiques, és a dir quan μr és molt proper a 1, i per tant, n és aproximadament . En aquest cas particular, la permitivitat relativa complexa εr, amb les parts reals i imaginàries εr i ɛ̃r, i l'índex de refracció complex n, amb les parts reals i imaginàries n i κ (aquest últim anomenat «coeficient d'extinció»), segueix la relació
i els seus components estan relacionats per:[33]
i
on és el mòdul complex.
En general, l'índex de refracció d'un vidre augmenta amb la seva densitat. No obstant això, no existeix una relació lineal global entre l'índex de refracció i la densitat de tots els vidres de silicat i de borosilicat. Un relatiu alt índex de refracció i una baixa densitat es poden obtenir amb els vidres que contenen òxids de metalls lleugers com ara Li₂O i MgO, mentre que la tendència oposada s'observa amb els vidres que contenen PbO i BaO.
Molts olis (com ara oli d'oliva) i l'alcohol etílic són exemples de líquids que són molt refractius, però menys densos que l'aigua, al contrari de la correlació general entre la densitat i l'índex de refracció.
Per als gasos, n - 1 és proporcional a la densitat del gas, sempre que la composició química no canviï.[34] Això vol dir que també és proporcional a la pressió i inversament proporcional a la temperatura per a gasos ideals.
De vegades, un «índex de refracció d'una velocitat de grup», normalment anomenat índex de grup, es defineix com
on vg és la velocidat de grup. Aquest valor no s'ha de confondre amb n, que sempre es defineix pel que fa a la velocitat de fase. Quan la dispersió és petita, la velocitat de grup pot vincular a la velocitat de fase per la relació[35]
on λ és la longitud d'ona en el medi. En aquest cas, l'índex de grup d'aquesta manera es pot escriure en termes de la longitud d'ona i l'índex de refracció com
Quan l'índex de refracció d'un medi es coneix com una funció de la longitud d'ona en el buit (en lloc de la longitud d'ona en el medi), les expressions corresponents per a la velocitat de grup i l'índex són (per a tots els valors de dispersió).[36]
on λ0 és la longitud d'ona en el buit.
En 1908 Hermann Minkowski va calcular la quantitat de moviment p d'un raig refractat de la següent manera:[37]
on E és l'energia del fotó, c és la velocitat de la llum en el buit, i n és l'índex de refracció del medi. En 1909 Max Abraham va proposar la següent fórmula per aquest càlcul:[38]
Un estudi de 2010 va suggerir que les dues equacions són correctes, amb la versió d'Abraham per al moment cinètic i la versió de Minkowski per al moment canònic, i pretenen explicar els resultats experimentals que contradiuen l'ús d'aquesta interpretació.[39]
En aplicacions atmosfèriques, la refractivitat es pren com a N = n - 1. La refractivitat atmosfèrica s'expressa sovint com a[40] N = 106(n – 1)[41][42] o N = 108(n – 1)[43] Els factors de multiplicació s'utilitzen a causa que l'índex de refracció en l'aire, n es desvia de la unitat com a màxim unes poques parts per deu mil.
D'altra banda, la refractivitat molar, és una mesura de la polaritzabilitat total d'un mol d'una substància i es pot calcular a partir de l'índex de refracció com
on ρ és la densitat, i M és la massa molar.[27]
Com es mostra en l'experiment de Fizeau, quan la llum es transmet a través d'un medi en moviment, la seva velocitat respecte a un observador estacionari és:
L'índex de refracció d'una substància pot estar relacionada amb la polaritzabilitat per l'equació Lorentz-Lorenz on la refractivitat molar dels seus components per la relació de Gladstone-Dale.
Fins al moment, hem assumit que la refracció està donada per les equacions lineals que impliquen un índex de refracció espacialment constant, escalar. Aquests supòsits es poden descompondre en diferents formes, que es descriuen en les següents subseccions.

En alguns materials, l'índex de refracció depèn de la direcció de polarització i la propagació de la llum.[44] Això es coneix com a birefringència o anisotropia òptica.

En la forma més simple, la birefringència uniaxial, només hi ha una direcció espacial en el material. Aquest eix és conegut com l'eix òptic del material.[45] La llum amb polarització lineal perpendicular a aquest eix experimentarà un índex de refracció ordinari no mentre que la llum polaritzada en paral·lel experimentarà un índex de refracció extraordinari ne .[46] La birefringència del material és la diferència entre aquests índexs de refracció, Δn = ne − no .[47] La llum que es propaga en la direcció de l'eix òptic no es veurà afectada per la birefringència, ja que l'índex de refracció no és independent de la polarització. Per a altres direccions de propagació de la llum, es divideix en dos feixos polaritzats linealment. Per la llum que viatja de forma perpendicular a l'eix òptic, els feixos tenen la mateixa direcció[48] Això pot utilitzar-se per a canviar la direcció de polarització de la llum polaritzada linealment o per convertir entre polaritzacions lineal, circular i el·líptica amb làmines d'ones.[47]
Molts cristalls són birrefringents naturals, però els materials isotròpics, com ara plàstics i vidres també poden fer-se sovint birrefringents mitjançant la introducció d'una direcció preferent a través de, per exemple, una força externa o camp elèctric. Això pot ser utilitzat en la determinació de les tensions en les estructures que utilitzen fotoelasticitat. Es col·loca el material birrefringent entre llums polaritzades creuades. Un canvi en la birefringència alterarà la polarització i per tant la fracció de llum que es transmet a través del segon polaritzador.
En el cas més general de materials trirefringents descrites pel camp de l'òptica cristal·lina, la constant dielèctrica és un tensor de rang 2 (una matriu de 3 per 3). En aquest cas, la propagació de la llum no pot simplement ser descrita per índexs de refracció a excepció de polaritzacions dels eixos principals.
El fort camp elèctric de la llum d'alta intensitat (com el produït per un làser) pot causar un índex de refracció al medi que varia quan la llum passa a través d'ell, donant lloc a l'òptica no lineal.[49]
Si l'índex varia cuadràticament amb el camp (de forma lineal amb la intensitat), s'anomena l'efecte Kerr òptic i provoca fenòmens com ara l'enfocament automàtic i automodulació de fase.[50]
Si l'índex varia linealment amb el camp (un coeficient lineal no trivial només és possible en els materials que no posseeixen simetria d'inversió), es coneix com a efecte Pockels.[51]

Si l'índex de refracció d'un medi que no és constant, sinó que varia gradualment amb la posició, el material es coneix com a gradient d'índex (o medi GRIN) i es descriu en l'òptica d'índex de gradient.[52]
La llum pot viatjar a través d'un medi on es pot doblegar o enfocar, i aquest efecte pot ser explotat per a produir lents, algunes fibres òptiques i altres dispositius. La introducció d'elements de GRIN en el disseny d'un sistema òptic pot simplificar en gran manera el sistema, reduint el nombre d'elements fins a un terç mentre es manté el rendiment general.[53]
El cristal·lí de l'ull humà és un exemple d'una lent GRIN amb un índex de refracció que varia aproximadament de 1,406 en el nucli intern fins a aproximadament 1,386 en l'escorça menys densa.[54]
Alguns miratges comuns són causats per un índex de refracció espacialment variable de l'aire.

L'índex de refracció de líquids o sòlids es pot mesurar amb refractòmetres. Solen mesurar un angle de refracció o l'angle crític per a la reflexió interna total.
Els primers refractòmetres de laboratori que es van vendre comercialment van ser desenvolupats per Ernst Abbe a finals del segle xix (vegeu Refractòmetre d'Abbe).[55] Actualment es segueixen utilitzant els mateixos principis. En aquest instrument, es col·loca una capa fina del líquid a mesurar entre dos prismes. Es projecta llum a través del líquid en tots els angles d'incidència fins al 90°, és a dir, fins que els raigs de llum són paral·lels a la superfície. El segon prisma hauria de tenir un índex de refracció més alt que el del líquid, de manera que la llum només entra en el prisma en angles més petits que l'angle crític per a la reflexió total. Aquest angle es pot mesurar ja sigui per mirant a través d'un telescopi, o amb un fotodetector digital col·locat en el pla focal d'una lent. L'índex de refracció n del líquid pot llavors calcular-se a partir de l'angle de transmissió màxima θ com n = nG sin θ, on nG és l'índex de refracció del prisma.[56]

Aquest tipus de dispositius s'utilitzen comunament en els laboratoris químics per a la identificació de substàncies i per al control de qualitat. Les variants manuals s'utilitzen en l'agricultura, per exemple, els fabricants de vi per a determinar el contingut de sucre en el suc del raïm, i els refractòmetres de procés en línia s'utilitzen en, per exemple, en la indústria química i farmacèutica per al control de processos.
En gemmologia s'utilitza un tipus diferent de refractòmetre per a mesurar l'índex de refracció i la birefringència de les pedres precioses. La gemma es col·loca en un prisma d'alt índex de refracció i s'il·lumina des de baix. S'utilitza un líquid de contacte amb un alt índex de refracció per aconseguir un contacte òptic entre la gemma i el prisma. En angles d'incidència petits la major part de la llum es transmetrà a la joia, però en angles alts es produirà una reflexió interna total en el prisma. L'angle crític es mesura normalment mirant per un telescopi.[57]
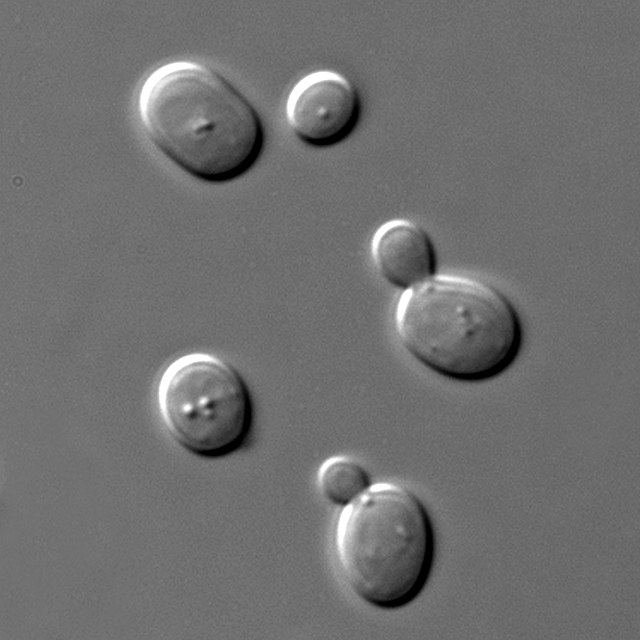
Les estructures biològiques no tenyides apareixen gairebé transparents sota microscòpia de camp brillant, com la majoria de les estructures cel·lulars que no redueixen les quantitats apreciables de llum. No obstant això, la variació en els materials que constitueixen aquestes estructures també corresponen a una variació en l'índex de refracció. Existeixen tècniques que converteixen aquesta variació en diferències d'amplitud mesurables.
Per mesurar la variació espacial d'índex de refracció en una mostra s'utilitzen mètodes d'imatge de contrast de fase. Aquests mètodes mesuren les variacions de fase de l'ona de llum que surt de la mostra. La fase és proporcional a la longitud del camí òptic del raig de llum que l'ha travessat, i per tant dona una mesura de la integral de l'índex de refracció al llarg de la trajectòria del raig. La fase no es pot mesurar directament en freqüències òptiques o en altes freqüències, i per tant ha de ser convertit en intensitat per interferència amb un feix de referència. En l'espectre visual això es fa utilitzant microscòpia de contrast de fase Zernike, microscòpia de contrast d'interferència diferencial (DIC) o interferometria.
Hi ha diverses tècniques de contrast de fase de formació d'imatges de raigs X per determinar una distribució espacial 2D o 3D de l'índex de refracció de mostres en el règim de raigs X.[58]

L'índex de refracció és una propietat molt important dels components de qualsevol instrument òptic que utilitza la refracció. Determina la potència d'enfocament de lents, el poder de dispersió de prismes, i en general la trajectòria de la llum a través del sistema. És l'augment de l'índex de refracció en el nucli que guia la llum en una fibra òptica, i les variacions en l'índex de refracció que redueix la reflectivitat d'una superfície tractada amb un revestiment antireflectant.
Com que l'índex de refracció és una propietat física fonamental d'una substància, sovint s'utilitza per identificar una substància particular, confirmar la seva puresa, o mesurar la seva concentració. L'índex de refracció s'utilitza per mesurar els sòlids, líquids i gasos. Més comunament s'usa per mesurar la concentració d'un solut en una solució aquosa. També es pot utilitzar com una eina útil per diferenciar entre diferents tipus de pedres precioses, a causa del chatoyance (efecte ull de gat) únic de cada mostra de pedra individual.
Un refractòmetre és l'instrument utilitzat per mesurar l'índex de refracció. Per a una solució de sucre, l'índex de refracció es pot utilitzar per determinar el contingut de sucre (vegeu escala Brix).
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.