Remove ads
La llum és la porció de l'espectre electromagnètic visible per a l'ull humà,[1] però en física el terme també pot ser utilitzat per a altres formes de radiació electromagnètica visible o no. La llum visible és aquella porció de l'espectre electromagnètic amb longituds d'ona entre aproximadament 380 nm i 780 nm (a l'aire) i una freqüència entre 789 terahertz (THz) i 385 THz.
 |
Per a altres significats, vegeu «Llum (desambiguació)». |
Les tres característiques bàsiques de la llum són la brillantor (o amplitud), el color (o freqüència) i la polarització (o angle de vibració). A causa de la dualitat ona-partícula, la llum presenta propietats tant d'ones com de partícules.
Remove ads
Les diferents longituds d'ona s'interpreten al cervell humà com a colors, des del vermell a les longituds d'ona més llargues (és a dir, a freqüències més baixes) fins al violat a les longituds d'ona més curtes (és a dir, a freqüències més altes). Les freqüències, en ordre creixent, es poden veure com a taronja, groc, verd, blau, i, convencionalment, blau indi:
| Color | Interval de longitud d'ona | Interval de freqüència | ||
|---|---|---|---|---|
| violat | ~ 380 a 430 nm | ~ 790 a 700 THz | ||
| blau | ~ 430 a 500 nm | ~ 700 a 600 THz | ||
| cian | ~ 500 a 520 nm | ~ 600 a 580 THz | ||
| verd | ~ 520 a 565 nm | ~ 580 a 530 THz | ||
| groc | ~ 565 a 590 nm | ~ 530 a 510 THz | ||
| taronja | ~ 590 a 625 nm | ~ 510 a 480 THz | ||
| vermell | ~ 625 a 740 nm | ~ 480 a 405 THz | ||
|
Espectre continu | ||||
Remove ads
La freqüència f i la longitud d'ona λ segueixen la relació:
- v = λ·f
on λ és la longitud d'ona, f la freqüència, i v la velocitat de la llum; per tant, la longitud d'ona i la freqüència són inversament proporcionals.
Si la llum viatja en el buit, llavors v = c, i així:
- c = λ·f
Tota la llum es propaga a una velocitat finita. Fins i tot els observadors en moviment uniforme mesuren sempre el mateix valor de c, la velocitat de la llum en el buit, com c = 299.792.458 m/s; de tota manera, quan la llum passa a través d'un medi transparent com aire, aigua o vidre, la seva velocitat es redueix, i pateix refracció.
Remove ads
Quan un feix de llum passa la frontera entre el buit i un altre medi, o entre dos medis diferents, la longitud d'ona de la llum canvia mentre que la freqüència roman constant. Si el feix de llum no és ortogonal a la frontera, la variació a la longitud d'ona provocarà un canvi de la direcció del feix. Aquest canvi de direcció és el que s'anomena refracció.
El canvi de direcció és més gran, com més gran és el canvi de rapidesa, ja que la llum prefereix recórrer les grans distàncies en el seu desplaçament pel mitjà que vagi més ràpid. La llei de Snell relaciona el canvi d'angle amb el canvi de rapidesa per mitjà dels índexs de refracció dels mitjans.
Com la refracció depèn de l'energia de la llum, quan es fa passar llum blanca o policromàtica a través d'un mitjà no paral·lel, com un prisma, es produeix la separació de la llum en els seus diferents components (colors) segons la seva energia, en un fenomen anomenat dispersió refractiva. Si el medi és paral·lel, la llum es torna a recompondre en sortir-ne.
Exemples molt comuns de la refracció són la ruptura aparent que es veu en un llapis a introduir-lo en aigua o l'arc de Sant Martí.
Remove ads
Els reflexos en superfícies planes, com ara un mirall o un got d’aigua, són simples. Un reflex apareix a la mateixa distància de la superfície reflectant que l’objecte original; la llum, a més, rebota en un angle igual al que ha estat emesa. És a dir: si el feix de llum s’emet en angle de noranta graus respecte a la superfície reflectant, aquesta tornarà a l’objecte emissor; en canvi, si s’emet amb una angulació de trenta graus per la dreta, rebotarà a trenta graus per l'esquerra.
En cas que la llum reboti en un mirall còncau o convex, però, els angles del reflex són diferents depenent del punt on reboti la llum. SI el mirall és convex, per exemple, es reflectirà una superfície més ampla, en què les imatges semblen més petites i més allunyades del que realment estan. És el cas, per exemple, dels retrovisors de cotxe. Si la superfície és còncava, en canvi, l'efecte és el contrari: generalment, rebotin on rebotin els rajos de llum, aquests són dirigits al punt central de la lent, anomenat punt focal, creant un augment de la imatge. És el cas, per exemple, de les lupes, els microscopis o els telescopis. El radi de curvatura de la lent és el que determina la distància focal o el nivell d’ampliació.
Remove ads
L'estudi de la llum i la seva interacció amb la matèria s'anomena òptica. L'observació i estudi de fenòmens òptics com els arcs de Sant Martí ofereix informació sobre la natura de la llum, a més de recreació.
La llum, en ser propagada a través d'un medi material, és absorbida progressivament. Per tant, transmet la seva energia al medi en el qual es propaga. Podem classificar aquests medis segons la capacitat d'absorció dels materials, en:
- Transparents: deixen passar fàcilment la llum, la llum es transmet a través d'aquest material, no és absorbida. En realitat no hi ha cap material totalment transparent.
- Opacs: no deixen passar gens la llum, l'absorbeixen totalment.
- Translúcids: deixen passar la llum, però de tal manera que les formes no es reconeixen.
Remove ads
La sensació de color és la manera com el nostre sistema visual interpreta les diferències en la longitud d'ona de la llum que li arriba.
Newton va demostrar, fent passar un raig de llum provenint del sol per un prisma,[3] que la llum blanca és una barreja de tots els colors de l'espectre visible, de totes les longituds d'ona.
Aquest experiment es basa en la propietat que l'angle de refracció entre aire i vidre (és a dir, l’angle de desviació de la llum en entrar al vidre) depèn de la longitud d'ona, cosa que fa que es "separin" els colors. Això és així perquè la velocitat de la llum en aquests medis és diferent per cada una de les longituds d'ona que, barrejades donen la llum blanca.
Amb aquesta experiència, Newton va ser el primer a veure explícitament l’espectre visible, la part de l'espectre electromagnètic que els nostres ulls perceben com a color. De fet, com és prou sabut, quan surt l'Arc de Sant Martí tothom té la possibilitat de veure aquest espectre: les gotetes d’humitat suspeses a l’aire després de ploure actuen com un conjunt de molts microprismes quan el sol surt i hi incideix.
Amb això ja sabem com és l’escenari lumínic en què acostumem a veure les coses. La llum del sol és blanca i per tant aquesta és la més abundant a la natura. Els objectes es veuen d'un determinat color perquè la seva superfície absorbeix una part de les longituds d'ona de la llum que l’il·lumina i reflecteix les altres. Les que predominen entre aquestes últimes donen la dominant de color d'un objecte doncs són les què arriben als nostres ulls quan el mirem.
Si una superfície absorbeix per igual tots els colors se'ns apareix com a gris. Si reflecteix molta llum serà blanquinosa, en cas contrari negrenca. Si una superfície reflecteix menys del 10% de la llum que li arriba ja ens sembla negra.
Amb el que acabem de dir resulta evident per què, si la llum que il·lumina els objectes no és blanca sinó que té una component cromàtica clarament dominant, el color amb què se'ns apareixerà resultarà completament alterat. Per tant, per definir el color d’un objecte cal que estigui il·luminat amb llum blanca.
A banda de tot això, cal no oblidar que la percepció i semantització del color és un fet marcadament cultural. Hi ha pobles el llenguatge dels quals només distingeix un parell de colors, mentre d'altres en parlen de centenars. En particular, és molt conegut el cas dels dani, un poble de Nova Guinea que tenen només dues paraules per designar els colors, mola i mili. De forma aproximada, car una traducció exacta és gairebé impossible, fan servir mola per parlar dels colors clars, i mili pels colors foscos, freds.
Remove ads
La llum presenta una naturalesa complexa: depèn de com s'observi es manifestarà com una ona o com una partícula. Aquests dos estats no s'exclouen, sinó que són complementaris (vegeu Dualitat ona-partícula). Tanmateix, per obtenir un estudi clar i concís de la seva naturalesa, es pot classificar els diferents fenòmens en els quals participa segons la seva interpretació teòrica:
Teoria ondulatòria
Descripció
Aquesta teoria considera que la llum és una ona electromagnètica, consistent en un camp elèctric que varia en el temps generant al seu torn un camp magnètic i viceversa, ja que els camps elèctrics variables generen camps magnètics (llei d'Ampère) i els camps magnètics variables generen camps elèctrics (llei de Faraday). D'aquesta manera, l'ona s'autopropaga indefinidament a través de l'espai, en camps magnètics i elèctrics generant contínuament. Aquestes ones electromagnètiques són sinusoidals, amb els camps elèctric i magnètic perpendiculars entre si i respecte a la direcció de propagació.
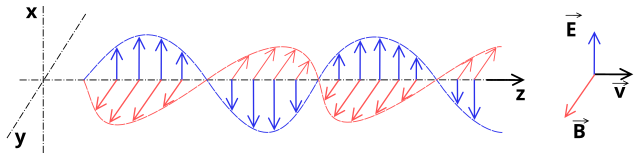
Per poder descriure una ona electromagnètica es poden utilitzar els paràmetres habituals de qualsevol ona:
- Amplitud (A): És la longitud màxima respecte a la posició d'equilibri que arriba l'ona en el seu desplaçament.
- Període (T): És el temps necessari per al pas de dos màxims o mínims successius per un punt fix en l'espai.
- Freqüència (v o f): Nombre d'oscil·lacions del camp per unitat de temps. És una quantitat inversa al període.
- Longitud d'ona (λ): És la distància lineal entre dos punts equivalents d'ones successives.
- Velocitat de propagació (V): És la distància que recorre l'ona en una unitat de temps. En el cas de la velocitat de propagació de la llum en el buit, es representa amb la lletra c.
La velocitat, la freqüència, el període i la longitud d'ona estan relacionades per les següents equacions:
Fenòmens ondulatoris
Alguns dels fenòmens més importants de la llum es poden comprendre fàcilment si es consideren que tenen un comportament ondulatori.
El principi de superposició d'ones permet explicar el fenomen de la interferència: si s'ajunten en el mateix lloc dues ones amb la mateixa longitud d'ona i amplitud, si estan en fase (les crestes de les ones coincideixen), formaran una interferència constructiva i la intensitat de l'ona resultant serà màxima i igual a dues vegades l'amplitud de les ones que la conformen. Si estan desfasades, hi haurà un punt on el desfasament serà màxim (la cresta de l'ona coincideixi exactament amb una vall) formant una interferència destructiva, anul·lant l'ona. L'experiment de Young, amb les seves escletxes, permet obtenir dos focus de llum de la mateixa longitud d'ona i amplitud, creant un patró d'interferències sobre una pantalla.
Les ones canvien la seva direcció de propagació en creuar un obstacle punxegut o en passar per una obertura estreta. Com recull el principi de Huygens, cada punt d'un front d'ones és un emissor d'un nou front d'ones que es propaguen en totes les direccions. La suma de tots els nous fronts d'ones fa que la pertorbació se segueixi propagant en la direcció original. Tanmateix, si per mitjà d'una escletxa o d'un obstacle punxegut, se separa un o uns pocs dels nous emissors d'ones, predominarà la nova direcció de propagació sobre l'original.
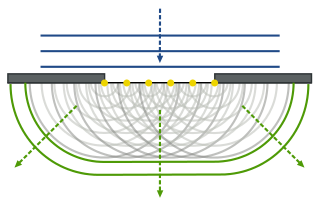
La difracció de la llum s'explica fàcilment si es té en compte aquest efecte exclusiu de les ones. La refracció, també es pot explicar utilitzant aquest principi, tenint en compte que les noves fronts d'ona generades en el nou mitjà, no es transmetran amb la mateixa velocitat que en l'anterior medi, generant una distorsió en la direcció de propagació:
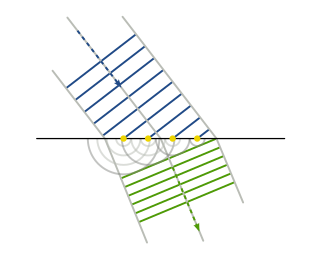
Un altre fenomen de la llum fàcilment identificable amb la seva naturalesa ondulatòria és la polarització. La llum no polaritzada està composta per ones que vibren en tots els angles; en arribar a un mitjà polaritzador, només les ones que vibren en un angle determinat aconsegueixen travessar el medi; en posar un altre polaritzador a continuació, si l'angle que deixa passar el mitjà coincideix amb l'angle de vibració de l'ona, la llum passarà íntegra; si no, només una part passarà fins a arribar a un angle de 90° entre els dos polaritzadors, on no passarà gens de llum.
Aquest efecte, a més, permet demostrar el caràcter transversal de la llum (les seves ones vibren en direcció perpendicular a la direcció de propagació).
L'efecte Faraday i el càlcul de la velocitat de la llum, c, a partir de constants elèctriques (permitivitat,) i magnètiques (permeabilitat, μ0) per part de la teoria de Maxwell: confirmen que les ones de les quals està composta la llum són de naturalesa electromagnètica. Aquesta teoria va ser capaç, també, d'eliminar la principal objecció a la teoria ondulatòria de la llum, que era trobar la manera com les ones es traslladaven sense un medi material.
Teoria corpuscular
Descripció
La teoria corpuscular estudia la llum com si es tractés d'un torrent de partícules sense càrrega i sense massa anomenats fotons, capaços de portar totes les formes de radiació electromagnètica. Aquesta interpretació ressorgeix a causa del fet que, la llum, en les seves interaccions amb la matèria, intercanvia energia només en quantitats discretes (múltiples d'un valor mínim) d'energia denominades quants. Aquest fet és difícil de combinar amb la idea que l'energia de la llum s'emet en forma d'ones, però és fàcilment visualitzat en termes de corpuscles de llum o fotons.
Fenòmens corpusculars
.jpg)
Existeixen tres efectes que demostren el caràcter corpuscular de la llum. Segons l'ordre històric, el primer efecte que no es va poder explicar per la concepció ondulatòria de la llum va ser la radiació del cos negre.
Un cos negre és un radiador teòricament perfecte que absorbeix tota la llum que incideix en ella i per això, quan s'escalfa es converteix en un emissor ideal de radiació tèrmica, que permet estudiar amb claredat el procés d'intercanvi d'energia entre radiació i matèria. La distribució de freqüències observades de la radiació emesa per la caixa a una temperatura de la cavitat donada, no es corresponia amb les prediccions teòriques de la física clàssica. Per poder explicar-ho, Max Planck, al començament del segle xx, va postular que per ser descrita correctament, s'havia d'assumir que la llum de freqüència ν és absorbida per múltiples sencers d'un quant d'energia igual a hν, on h és una constant física universal anomenada Constant de Planck.
El 1905, Albert Einstein va utilitzar la teoria quàntica desenvolupada per Planck per explicar un altre fenomen no comprès per la física clàssica: l'efecte fotoelèctric. Aquest efecte consisteix en el fet que quan un feix monocromàtic de radiació electromagnètica il·lumina la superfície d'un sòlid (i, de vegades, la d'un líquid), es desprenen electrons en un fenomen conegut com a fotoemissió o efecte fotoelèctric extern. Aquests electrons tenen una energia cinètica que pot ser mesura electrònicament amb un col·lector amb càrrega negativa connectat a la superfície emissora. No es podia entendre que l'emissió dels anomenats "fotoelectrons" fos immediata i independent de la intensitat del raig. Eren fins i tot capaços de sortir acomiadats amb intensitats extremadament baixes, el que excloïa la possibilitat que la superfície acumulada d'alguna manera l'energia suficient per disparar els electrons. A més, el nombre d'electrons era proporcional a la intensitat del raig incident. Einstein va demostrar que l'efecte fotoelèctric podia ser explicat assumint que la llum incident estava formada de fotons d'energia hν, part d'aquesta energia hν0 es feia servir per trencar les forces que unien l'electró amb la matèria, la resta de l'energia apareixia com l'energia cinètica dels electrons mesos:
on m és la massa de l'electró, Vmax la velocitat màxima observada, ν és la freqüència de la llum il·luminant i ν0 és la freqüència llindar característica del sòlid emissor.
La demostració final va ser aportada per Arthur Compton que va observar com en fer incidir raigs X sobre elements lleugers, aquests es dispersen amb menys energia i més electrons es desprenen (fenomen posteriorment denominat en el seu honor com a efecte Compton). Compton, ajudant-se de les teories anteriors, va donar una explicació satisfactòria al problema tractant la llum com a partícules que xoquen elàsticament amb els electrons com dues boles de billar. El fotó, corpuscle de llum, colpeja l'electró: l'electró surt disparat amb una part de l'energia del fotó i el fotó reflecteix la seva menor energia en la seva freqüència. Les direccions relatives en les quals surten tots dos estan d'acord amb els càlculs de la conservació de l'energia i el moment.
Teories quàntiques
La necessitat de reconciliar les equacions de Maxwell del camp electromagnètic, que descriuen el caràcter ondulatori electromagnètic de la llum, amb la naturalesa corpuscular dels fotons, ha fet que apareguin diverses teories que estan encara lluny de donar un tractament unificat satisfactori. Aquestes teories incorporen d'una banda, la teoria de l'electrodinàmica quàntica, desenvolupada a partir dels articles de Dirac, Jordan, Heisenberg i Pauli, i per altra banda la mecànica quàntica de De Broglie, Heisenberg i Schrödinger.
Paul Dirac va donar el primer pas amb la seva equació d'ones que va aportar una síntesi de les teories ondulatòria i corpuscular, ja que sent una equació d'ones electromagnètiques seva solució requeria ones quantificades, és a dir, partícules. La seva equació consistia a reescriure les equacions de Maxwell de tal manera que s'assembla a les equacions hamiltonians de la mecànica clàssica. A continuació, utilitzant el mateix formalisme que, a través de la introducció del que fa d'acció hν, transforma les equacions de mecànica clàssica en equacions de mecànica ondulatòria, Dirac va obtenir una nova equació del camp electromagnètic. Les solucions a aquesta equació requerien ones quantificades, subjectes al principi d'incertesa de Heisenberg, la superposició representaven el camp electromagnètic. Gràcies a aquesta equació es pot conèixer una descripció de la probabilitat que passi una interacció o observació donada, en una regió determinada.
Encara hi ha moltes dificultats teòriques sense resoldre, però, la incorporació de noves teories procedents de l'experimentació amb partícules elementals, així com de teories sobre el comportament dels nuclis atòmics, ens han permès obtenir una formulació addicional de gran ajuda.
Efectes relativistes
Tanmateix, hi havia encara algunes situacions en què la llum no es comportava segons s'esperava per les teories anteriors.
Llum en moviment
La primera d'aquestes situacions inexplicables es produïa quan la llum s'emetia, es transmetia o es rebia per cossos o mitjans en moviment. Era d'esperar, segons la física clàssica, que la velocitat en aquests casos fos el resultat de sumar a la velocitat de la llum, la velocitat del cos o del medi. Tanmateix, es van trobar diversos casos en què no era així:
El 1818, Augustin Fresnel va proposar un experiment per mesurar la velocitat a la qual la llum travessava un líquid en moviment. Per a això, es faria travessar a la llum una columna d'un líquid que fluís a una velocitat v relativa a l'observador. Coneixent la velocitat v' a la qual es transmet la llum a través d'aquest mitjà (a través de l'índex de refracció), es va calcular que la velocitat total de la llum en aquest fluid seria:
Tanmateix, quan el 1851, el físic francès Hippolyte Fizeau va dur a terme l'experiment, va comprovar que la velocitat a la qual la llum travessava el líquid en moviment no era la calculada sinó:
És a dir, que la velocitat del fluid comptava menys a la velocitat final si la velocitat amb la qual travessava la llum aquest fluid era major.
El 1725, James Bradley va descobrir que la posició observada de les estrelles en el firmament variava anualment respecte a la posició real en un interval de 41 segons de l'arc. La teoria que va proposar per explicar va ser que aquesta variació es devia a la combinació de la velocitat de la terra al girar al voltant del sol amb la velocitat finita de la llum. Gràcies a aquesta teoria va ser capaç de calcular la velocitat de la llum d'una forma acceptable. Basant-se en aquest efecte, l'astrònom anglès George Airy comparar l'angle d'aberració en un telescopi abans i després d'omplir d'aigua, i va descobrir que, en contra de les seves expectatives, no hi havia diferències en les seves mesures (la llum no variava de velocitat a tot i que el fluid es mogui a la velocitat de la terra).
Tenint en compte aquest experiment, dos astrònoms, l'alemany Albert Michelson i el nord-americà Edward Morley van proposar un experiment (vegeu Experiment de Michelson i Morley) per mesurar la velocitat a la qual fluïa l'èter respecte a la terra. Suposaven que l'èter es movia en una direcció concreta amb una velocitat determinada, per això, a causa de la translació de la Terra al voltant del Sol hauria èpoques de l'any en què tindríem una component d'aquesta velocitat a favor i altres èpoques en contra, pel que van suposar que quan ho tinguéssim a favor, la velocitat de la llum seria superior i quan ho tinguéssim en contra seria inferior. Per a això van mesurar la velocitat de la llum en diferents estacions de l'any i van observar que no hi havia cap diferència. I el més curiós: que ni tan sols havia diferències degudes a la mateixa velocitat de translació de la Terra (30 km/s).
En 1905, Albert Einstein va donar una explicació satisfactòria amb la seva teoria de la relativitat especial, en la qual, en el seu segon postulat proposa que la velocitat de la llum és isotropia, és a dir, independent del moviment relatiu de l'observador o de la font.
Distorsions espectrals
En comparar l'espectre de la llum procedent d'alguns cossos celestes, amb els espectres mesurats en el laboratori dels mateixos elements que els que contenen aquests cossos, s'observa que no són iguals, ja que les línies espectrals procedents de l'espai estan desplaçades cap a posicions de major longitud d'ona, és a dir, cap al costat vermell de l'espectre en llocs de menor energia.
S'han trobat dos tipus diferents de desplaçaments de línies espectrals:
Un, el més comú, anomenat desplaçament nebular és un desplaçament sistemàtic dels espectres procedents de les estrelles i galàxies. Edwin Hubble després d'estudiar el corriment dels espectres de les nebuloses, ho va interpretar com el resultat de l'efecte Doppler degut a l'expansió contínua de l'univers. Gràcies a això va proposar una fórmula capaç de calcular la distància que ens separa d'un cos determinat analitzant el corriment del seu espectre:
on Δλ és la diferència entre les longituds d'ona de l'espectre del cos i l'esperada, λ és la longitud d'ona esperada i d, la distància en parsecs.
L'altre, molt més estrany s'anomena desplaçament gravitacional o efecte Einstein, observat en espectres de cossos extremadament densos. L'exemple més famós és l'espectre de l'anomenat company fosc de Sírius. L'existència d'aquest company va ser predita per Friedrich Bessel el 1844 basant-se en una pertorbació que va observar en el moviment de Sírius, però a causa de la seva feble lluminositat, no va ser descobert fins a 1861. Aquest company és una nana blanca que té una massa comparable a la del Sol però en un radi aproximadament cent vegades menor, per la qual cosa la seva densitat és immensa (61.000 vegades la de l'aigua). A l'estudiar el seu espectre, s'observa un desplaçament de 0,3 Å de la línia β de la sèrie Balmes l'hidrogen.
Teoria de la relativitat general
Perquè la seva anterior teoria de la relativitat especial abasta també els fenòmens gravitatoris, Albert Einstein, entre 1907 i 1915 va desenvolupar la teoria de la relativitat general. Una de les principals conclusions d'aquesta teoria és que la propagació de la llum està influenciada per la gravetat, representada en la teoria pel potencial gravitatori Φ, descrit per
on G és la Constant de gravitació universal, M la massa i R el radi del cos
Einstein va trobar que la llum, al passar per un camp gravitatori de potencial Φ patia una disminució de la seva velocitat, segons la fórmula:
on c0 és la velocitat de la llum sense camp gravitatori i c és la velocitat amb ell.
També es veu modificada la freqüència de la llum emesa per una font en un camp gravitatori
el que explica el desplaçament gravitacional. Un altre exemple que confirma experimentalment aquest punt de la teoria són les línies espectrals del sol, que estan desplaçades cap al vermell dues milionèsimes vegades quan sigui comparen amb les generades pels mateixos elements en la Terra.
Finalment, en aquesta relació entre llum i gravetat, aquesta teoria va predir que els raigs de llum al passar prop d'un cos pesant es desviava un angle α determinat per l'efecte del seu camp gravitatori, segons la relació:
Aquest punt de la teoria va ser confirmat experimentalment estudiant el desviament de la llum que provocava el Sol, per això els científics van estudiar la posició de les estrelles de l'àrea al voltant del sol aprofitant un eclipsi el 1931. Es va veure que, com predeia la teoria, estaven desviades fins a 2,2 segons d'arc comparades amb fotografies de la mateixa àrea 6 mesos abans.
Radiació i matèria
Al formular la seva equació d'ones per un electró lliure, Paul Dirac va predir que era possible crear un parell d'electrons (un carregat positivament i l'altre negativament) a partir d'un camp electromagnètic que vibri amb una rapidesa extrema. Aquesta teoria va ser ràpidament confirmada pels experiments d'Irene Curie i Frédéric Joliot i pels de James Chadwick, Stuart Blackett i Giuseppe Occhialini en comparar el nombre d'electrons amb càrrega negativa i el nombre d'electrons amb càrrega positiva (aquests darrers anomenats positrons) despresos pels raigs γ d'alta freqüència en travessar primes làmines de plom i descobrir que s'obtenia la mateixa quantitat d'uns que dels altres.
Aviat es van trobar altres maneres de crear parells positró-electró i avui en dia es coneixen una gran quantitat de mètodes:
- Fent xocar dues partícules pesants
- Fent passar a un electró a través del camp d'un nucli atòmic
- La col·lisió directa de dos electrons
- La col·lisió directa de dos fotons en el buit
- L'acció del camp d'un nucli atòmic sobre un raig γ emès pel mateix nucli.
També passa el procés en sentit contrari: en topar un electró i un positró (ells sols tendeixen a ajuntar-se, ja que tenen càrregues elèctriques oposades), tots dos s'aniquilen convertint tota la seva massa en energia radiant. Aquesta radiació s'emet en forma de dos fotons de raigs γ dispersats en la mateixa direcció, però diferent sentit.
Aquesta relació entre matèria i radiació, i radiació i matèria (i sobretot la conservació de l'energia en aquesta classe de processos) està descrita en la famosa equació d'Albert Einstein.
emmarcada en la teoria de la relativitat especial i que originalment va formular així:
| « | Si un cos de massa m desprèn una quantitat d'energia E en forma de radiació, la seva massa disminueix E/c² | » |
| — Albert Einstein a Zur Elektrodynamik bewegter Körper[4] | ||
Teories de camp unificat
Actualment, es busca una teoria que sigui capaç d'explicar de forma unificada la relació de la llum, com a camp electromagnètic, amb la resta de les interaccions fonamentals de la natura. Les primeres teories intentar representar l'electromagnetisme i la gravitació com aspectes de la geometria espaitemps, i encara que existeixen algunes evidències experimentals d'una connexió entre l'electromagnetisme i la gravitació, només s'han aportat teories especulatives.
Els estudis científics d'objectes basats en l'espectre de llum que emeten és anomenat espectroscòpia. Una aplicació particularment important d'aquest estudi és en l'astronomia on els espectroscopis són essencials per a analitzar propietats d'objectes distants. L'espectroscòpia astronòmica utilitza difracció d'alta dispersió per a observar espectres de moltes altres resolucions espectrals. L'heli va ser el primer que es va detectar en l'anàlisi de l'espectre del sol; els elements químics poden ser detectats en objectes astronòmics per les línies espectrals i les línies d'absorció; la mesura de línies espectrals pot ser utilitzada com a mesura de desplaçament cap al roig o desplaçament cap al blau d'objectes distants que es mouen a altes velocitats. El primer exoplaneta a ser descobert per l'anàlisi de l'efecte Doppler d'estrelles a les quals la seva alta resolució que variava la seva velocitat radial tan petita com uns pocs metres per segon podrien ser detectades: la presència de planetes va ser revelada per la seva influència gravitacional en les estrelles analitzades.
L'espectre electromagnètic està constituït per tots els diferents nivells d'energia que la llum pot prendre. Parlar d'energia és equivalent a parlar de la longitud d'ona; després, l'espectre electromagnètic abasta, també, totes les longituds d'ona que la llum pugui tenir, des de milers de quilòmetres fins femtòmetres. És per això que la major part de les representacions esquemàtiques de l'espectre solen tenir escala logarítmica.
L'espectre electromagnètic es divideix en regions espectrals, classificades segons els mètodes necessaris per a generar i detectar els diversos tipus de radiació. És per això que aquestes regions no tenen una frontera definida i hi ha algunes superposicions entre elles.
Espectre visible
De tot l'espectre, la porció que l'ésser humà és capaç de veure és molt petita en comparació amb les altres regions espectrals. Aquesta regió, anomenada espectre visible, comprèn longituds d'ona des dels 380 nm fins als 780 nm. La llum de cadascuna d'aquestes longituds d'ona és percebuda per l'ull humà com un color diferent, per això, en la descomposició de la llum blanca en totes les seves longituds d'ona, per prismes o per la pluja en l'arc de Sant Martí, l'ull veu tots els colors.
La llum es mesura amb dos conjunts principals d'unitats: la radiometria mesura la potència de la llum en totes les longituds d'ona, mentre que la fotometria mesura la capacitat que té la radiació electromagnètica d'estimular l'ull humà. La fotometria és adequada, per exemple, per quantificar la potència dels sistemes d'il·luminació destinats a ús humà. Les unitats SI per a ambdós sistemes es resumeixen en les següents taules.
| Magnitud física | Símbol | Unitat del SI | Abreviat | Notes |
|---|---|---|---|---|
| Energia radiant | Q | joule | J | energia |
| Flux radiant | Φ | watt | W | Energia radiada per unitat de temps. Potència. |
| Intensitat radiant | I | watt per estereoradiant | W·sr−1 | Potència per unitat d'angle sòlid |
| Radiància | L | watt per estereoradiant per metre quadrat | W·sr−1·m−2 | Potència. Flux radiant emès per unitat de superfície i per angle sòlid |
| Irradiància | E | watt per metre quadrat | W·m−2 | Potència incident per unitat de superfície |
| Exitància radiant | M | watt per metre quadrat | W·m−2 | Potència emesa per unitat de superfície de la font radiant |
| Radiància espectral | Lλ o Lν |
watt per estereoradiant per metre cúbic o
|
W·sr−1·m−3
o |
Intensitat d'energia radiada per unitat de superfície, longitud d'ona i angle sòlid. Habitualment mesurada en W·sr−1·m−2·nm−1 |
| Irradiància espectral | Eλ o |
watt per metre cúbic o
watt per metre quadrat per hertz |
W·m−3 o |
Habitualment mesurada en W·m−2·nm−1 |
| Magnitud fotomètrica | Símbol | Unitat | Abreviatura | Magnitud radiomètrica associada |
| Quantitat de llum o energia lluminosa | lumen·segon | lm·s | Energia radiant | |
| Flux lluminós o potència lluminosa | lumen (= cd·sr) | lm | Flux radiant o potència radiant | |
| Intensitat lluminosa | candela | cd | Intensitat radiant | |
| Luminància | candela /metre² | cd /m² | Radiància | |
| Il·luminació | lux | lx | Irradiància | |
| Emitància lluminosa | lux | lx | Emitància radiant | |
Les associacions culturals de la llum acostumen a oposar-la a la foscor, de manera que les connotacions de la llum són positives i les de la foscor, negatives. Així, la llum s'associa al bé mentre que els éssers de tenebres o de la nit tenen a veure amb el mal i el diable. Igualment la llum té a veure amb la raó, les idees, la comprensió (es parla d'il·luminació quan s'assoleix el màxim enteniment o harmonia amb la divinitat o el món) i també l'alegria.
- Atkins, Peter; de Paula, Julio. «Quantum theory: introduction and principles». A: Physical Chemistry. Nova York: Oxford University Press, 2002. ISBN 0-19-879285-9.
- Skoog, Douglas A.; Holler, F. James; Nieman, Timothy A.. «Introducción a los métodos espectrométricos». A: Principios de Análisis instrumental. 5a Edición. Madrid: McGraw-Hill, 2001. ISBN 84-481-2775-7.
- Tipler, Paul Allen. Física. 3a Edición. Barcelona: Reverté, 1994. ISBN 84-291-4366-1.
- Burke, John Robert. Física: la naturaleza de las cosas. México DF: International Thomson Editores, 1999. ISBN 968-7529-37-7.
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
Remove ads