Resistència de materials

La resistència de materials és una disciplina que tracta el comportament dels objectes sota l'acció de tensions i deformacions. S'estudien els mètodes per calcular tensions en membres estructurals (com bigues, columnes, etc.) i, d'aquesta manera, poder predir com es comportarà l'estructura sota càrregues i com serà de susceptible a fallar tenint en compte les propietats del material.

Les línies de força internes són més denses prop del forat: es tracta d'una concentració de tensions molt comuna

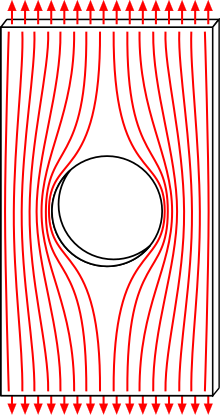
Un model de resistència de materials estableix una relació entre les forces aplicades, també anomenades càrregues o accions, i els esforços i desplaçaments induïts per elles. Generalment, les simplificacions geomètriques i les restriccions imposades sobre el mode d'aplicació de les càrregues fan que el camp de deformacions i tensions siguin senzills de calcular.

Pel disseny mecànic d'elements amb geometries complicades, la resistència de materials sol ser abundant i cal utilitzar tècniques basades en la teoria de l'elasticitat o la mecànica de sòlids deformables més generals. Aquests problemes plantejats en termes de tensions i deformacions poden llavors ser resolts de forma molt aproximada amb mètodes numèrics com l'anàlisi per elements finits.

Definicions

En ciència de materials, la resistència d'un material és la seva capacitat d'aguantar una tensió aplicada sense fallar. Una càrrega aplicada sobre un membre mecànic induirà forces internes dins seu (anomenades tensions), que poden provocar-li deformacions. La tensió aplicada pot ser de tracció, de compressió o tallant.

Tipus de càrregues

• Càrrega transversal: força aplicada perpendicularment a l'eix longitudinal de l'element. Aquesta càrrega causa la flexió del membre i es produeixen tensions internes de tracció i compressió.^[1] També s'indueixen forces tallants.
• Càrrega axial: força aplicada colinealment a l'eix longitudinal de l'element, el qual s'allarga o es comprimeix (no hi ha flexió).^[2]
• Càrrega de torsió: acció de gir causada per un parell de forces extern aplicat sobre un element que té un dels dos extrems fixat.

Tensions

Material carregat amb a) compressió, b) tracció, c) tallant

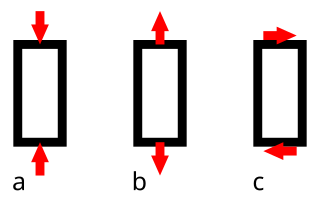
La tensió uniaxial s'expressa així:

${\displaystyle \sigma ={\frac {F}{A}},}$

On F és la força [N] que actua sobre una àrea A [m²].^[3] Aquesta àrea pot ser sense deformar o deformada.

• La tensió de compressió és l'estat de tensions causat per una càrrega aplicada que actua intentant reduir la llargada del material al llarg de l'eix on s'aplica dita càrrega. Un cas simple de compressió és la compressió uniaxial, causada per l'acció de dues forces oposades. La resistència a compressió dels materials sol ser més elevada que la seva resistència a tracció; tanmateix, les estructures sotmeses a compressió són més proclius a fallar per teories que depenen de la geometria, com el vinclament.
• La tensió de tracció és l'estat de tensions causat per una càrrega aplicada que actua intentant allargar el material al llarg de l'eix de la càrrega aplicada. Els materials carregats amb tensions de tracció són susceptibles a les concentracions de tensions que es produeixen en zones amb defectes materials, per exemple. Els materials dúctils (com la majoria de metalls) poden tolerar alguns defectes, mentre que els materials fràgils (com la ceràmica) poden fallar molt abans.
• La tensió tallant és l'estat de tensions causat per forces oposades que actuen en línies paral·leles d'acció a través del material, en altres paraules, és l'estat de tensions causat per les cares del material "lliscant" relativament una a l'altra. Un exemple és el tall de paper amb les tisores^[4] o les tensions causades per una càrrega a torsió.

Resistències

• El límit de fluència és la tensió mínima que produeix una deformació permanent del material. En alguns materials, com ara aliatges de l'alumini, el punt de fluència és difícil d'identificar, per la qual cosa se sol definir com la tensió necessària per causar un 0,2% de deformació plàstica.^[5]

• La resistència a compressió és el límit que pot aguantar l'element a tensió de compressió. Un cop sobrepassat pot fallar per fractura dúctil o per fractura fràgil.
• La resistència a tracció és el límit que pot aguantar l'element a tensió de tracció. Un cop sobrepassat pot fallar per fractura dúctil o per fractura fràgil.
• El límit de fatiga o resistència a fatiga mesura de la resistència d'un material o component sota una càrrega cíclica.^[6] Sol ser més difícil de determinar que les mesures de resistència estàtica. La resistència a fatiga es dona en forma d'amplitud o rang de tensions (${\displaystyle \Delta \sigma =\sigma _{\mathrm {max} }-\sigma _{\mathrm {min} }}$), normalment amb la mitjana de tensions a zero, juntament amb el nombre de cicles per fallar sota aquesta condició d'estat de tensions.

• La resistència a l'impacte és la capacitat del material per aguantar una càrrega aplicada sobtadament. S'expressa en termes d'energia. Es mesura amb l'assaig d'Izod o amb el de Charpy. La resistència a l'impacte sol veure's afectada pel volum, mòdul d'elasticitat, distribució de forces i límit de fatiga. Vegeu també: resiliència.

Deformacions

• La deformació d'un material és el canvi de geometria que pateix quan se li aplica un estat de tensions.^[7]
• La deformació unitària és el terme matemàtic que expressa la proporció de deformació que ha sofert l'element (deformació per unitat de longitud).^[8]
• La fletxa és un terme que descriu com es flexiona un element estructural quan se li aplica una càrrega.^[9]

Relacions tensió-deformació

Resposta d'un element sotmès a un estat tensional

• L'elasticitat és la capacitat d'un material per tornar a la seva forma anterior un cop es deixa d'aplicar l'estat tensional. En molts materials, la relació entre la tensió aplicada i la deformació resultant és directament proporcional (fins a un cert límit). El pendent de la línia recta resultant de representar aquestes dues quantitats és el mòdul d'elasticitat.^[10]
• La plasticitat és el contrari de la deformació elàstica. Quan un material es deforma plàsticament (després de superar el seu límit de fluència no pot tornar a la seva forma anterior.

Equacions d'equilibri

Les equacions d'equilibri de la resistència de materials relacionen els esforços interns amb les forces exteriors aplicades. Les equacions d'equilibri per a elements lineals i elements bidimensionals són el resultat d'escriure les equacions d'equilibri elàstic en termes dels esforços en lloc de les tensions.

Les equacions d'equilibri per al camp de tensions generals de la teoria de l'elasticitat lineal:

${\displaystyle {\frac {\partial \sigma _{xx}}{\partial x}}+{\frac {\partial \sigma _{xy}}{\partial y}}+{\frac {\partial \sigma _{xz}}{\partial z}}=b_{x}}$

${\displaystyle {\frac {\partial \sigma _{yx}}{\partial x}}+{\frac {\partial \sigma _{yy}}{\partial y}}+{\frac {\partial \sigma _{yz}}{\partial z}}=b_{y}}$

${\displaystyle {\frac {\partial \sigma _{zx}}{\partial x}}+{\frac {\partial \sigma _{zy}}{\partial y}}+{\frac {\partial \sigma _{zz}}{\partial z}}=b_{z}}$

Si s'hi tracta de substituir les tensions pels esforços interns, s'arriba llavors a les equacions d'equilibri de la resistència de materials. El procediment, que es detalla a continuació, és lleugerament diferent per a elements unidimensionals i bidimensionals.

Equacions d'equilibri en elements lineals rectes

En una biga recta horitzontal, alineada amb l'eix X, i on les càrregues són verticals i situades sobre el pla XY, les equacions d'equilibri relacionen el moment flector (M_z), l'esforç tallant (V_y) amb la càrrega vertical (q_y) i tenen la forma:

${\displaystyle {\frac {dM_{z}}{dx}}=V_{y}\qquad \land \qquad {\frac {dV_{y}}{dx}}=-q_{y}\qquad \Rightarrow \qquad {\frac {d^{2}M_{z}}{dx^{2}}}=-q_{y}}$

Equacions d'equilibri en elements plans bidimensionals

Les equacions d'equilibri per a elements bidimensionals (plaques) en flexió anàlogues a les equacions de la secció anterior per a elements lineals (bigues) relacionen els moments per unitat d'amplada (m_x, m_y, m_xy), amb els esforços tallants per unitat d'amplada (v_x, m_y) i la càrrega superficial vertical (q_s):

${\displaystyle {\begin{matrix}{\cfrac {\partial m_{x}}{\partial x}}+{\cfrac {\partial m_{xy}}{\partial y}}=v_{x}\\{\cfrac {\partial m_{xy}}{\partial x}}+{\cfrac {\partial m_{y}}{\partial y}}=v_{y}\end{matrix}}\quad \land \quad {\frac {\partial v_{x}}{\partial x}}+{\frac {\partial v_{y}}{\partial y}}=-q_{s}\qquad \Rightarrow \qquad {\frac {\partial ^{2}m_{x}}{\partial x^{2}}}+2{\frac {\partial ^{2}m_{xy}}{\partial y\partial x}}+{\frac {\partial ^{2}m_{y}}{\partial y^{2}}}=-q_{s}}$

Relació entre esforços i desplaçaments

Un altre problema important en moltes aplicacions de la resistència de materials és l'estudi de la rigidesa. Més concretament certes aplicacions requereixen assegurar que sota les forces actuants alguns elements resistents no superin mai desplaçaments per sobre de cert valor prefixat. El càlcul de les deformacions a partir dels esforços es pot determinar mitjançant diversos mètodes semidirectes com l'ús del teorema de Castigliano, les fórmules vectorials de Navier-Bresse, l'ús de l'equació de la corba elàstica, el mètode matricial de la rigidesa i altres mètodes numèrics per als casos més complexos.

Termes de disseny

La força màxima és un atribut relacionat amb un material, en lloc d'una mostra específica feta del material, i com a tal es cita com la força per unitat d'àrea de secció transversal (N/m²). La força màxima és la tensió màxima que pot suportar un material abans que es trenqui o es debiliti.^[11] Per exemple, la resistència a la tracció màxima (UTS) de l'acer AISI 1018 és de 440 MPa. A les unitats imperials, la unitat de tensió es dóna com a lbf/in² o lliures de força per polzada quadrada. Aquesta unitat s'abreuja sovint com a psi. Mil psi s'abreuja ksi.

Un coeficient de seguretat és un criteri de disseny que ha d'aconseguir un component o una estructura d'enginyeria. ${\displaystyle FS=UTS/R}$, on FS: el coeficient de seguretat, R: l'estrès aplicat i UTS: estrès final (psi o N/m²).^[12]

El marge de seguretat també s'utilitza de vegades com a criteri de disseny. Es defineix MS = Càrrega de fallada/(Coeficient de seguretat × Càrrega prevista) − 1.

Per exemple, per aconseguir un coeficient de seguretat de 4, la tensió admissible en un component d'acer AISI 1018 es pot calcular com a ${\displaystyle R=UTS/FS}$ = 440/4 = 110 MPa, o ${\displaystyle R}$ = 110×10⁶ N/m². Aquestes tensions permeses també es coneixen com a "esforços de disseny" o "esforços de treball".

Les tensions de disseny que s'han determinat a partir dels valors finals o de límit de fluència dels materials donen resultats segurs i fiables només en el cas de càrrega estàtica. Moltes peces de la màquina fallen quan se sotmeten a càrregues no constants i variables contínuament tot i que les tensions desenvolupades estan per sota del límit de fluència. Aquestes fallades s'anomenen fallades per fatiga. El fracàs és per una fractura que sembla fràgil amb poca o cap evidència visible de cediment. Tanmateix, quan l'estrès es manté per sota de l′"estrès de fatiga" o "estrès límit de resistència", la peça aguantarà indefinidament. Una tensió purament inversa o cíclica és aquella que alterna entre tensions pics positives i negatives iguals durant cada cicle d'operació. En una tensió purament cíclica, la tensió mitjana és zero. Quan una peça està sotmesa a una tensió cíclica, també coneguda com a rang de tensió (Sr), s'ha observat que la fallada de la peça es produeix després d'una sèrie d'inversions de tensió (N) encara que la magnitud de l'interval de tensió sigui inferior al límit de fluència del material. En general, com més gran sigui la tensió del rang, menor serà el nombre d'inversions necessàries per a la fallada.

Teories de fallades

Hi ha quatre teories de fallada: teoria de l'esforç de cisalla màxima, teoria de l'esforç normal màxim, teoria de l'energia de deformació màxima i teoria de l'energia de la màxima distorsió. D'aquestes quatre teories de fallada, la teoria de l'estrès normal màxim només s'aplica als materials fràgils, i les tres teories restants són aplicables als materials dúctils. D'aquests tres últims, la teoria de l'energia de distorsió proporciona els resultats més precisos en la majoria de les condicions d'estrès. La teoria de l'energia de deformació necessita el valor del coeficient de Poisson del material de la peça, que sovint no és fàcilment disponible. La teoria de l'esforç de tall màxim és conservadora. Per a tensions normals unidireccionals simples, totes les teories són equivalents, el que significa que totes les teories donaran el mateix resultat.

• Teoria de l'esforç de cisalla màxima: aquesta teoria postula que la fallada es produirà si la magnitud de l'esforç de cisalla màxima de la peça supera la resistència a tall del material determinada a partir de proves uniaxials.
• Teoria de la tensió normal màxima: aquesta teoria postula que la fallada es produirà si la tensió normal màxima de la peça supera l'esforç de tracció final del material determinat a partir de proves uniaxials. Aquesta teoria només tracta de materials trencadissos. L'esforç de tracció màxim ha de ser inferior o igual a l'esforç de tracció final dividit pel coeficient de seguretat. La magnitud de la tensió de compressió màxima hauria de ser inferior a la tensió de compressió final dividida pel coeficient de seguretat.
• Teoria de l'energia de deformació màxima: aquesta teoria postula que la fallada es produirà quan l'energia de deformació per unitat de volum a causa de les tensions aplicades en una peça sigui igual a l'energia de deformació per unitat de volum en el punt de fluència en les proves uniaxials.
• Teoria de l'energia de distorsió màxima: aquesta teoria també es coneix com a teoria de l'energia de cisalla o Teoria de von Mises-Hencky. Aquesta teoria postula que la fallada es produirà quan l'energia de distorsió per unitat de volum a causa de les tensions aplicades en una part sigui igual a l'energia de distorsió per unitat de volum en el punt de fluència en les proves uniaxials. L'energia elàstica total deguda a la deformació es pot dividir en dues parts: una part provoca un canvi de volum i l'altra part provoca un canvi de forma. L'energia de distorsió és la quantitat d'energia que es necessita per canviar la forma.
• La mecànica de fractures va ser establerta per Alan Arnold Griffith i George Rankine Irwin. Aquesta important teoria també es coneix com a conversió numèrica de la duresa del material en el cas de l'existència d'esquerdes.

La força d'un material depèn de la seva microestructura. Els processos d'enginyeria als quals està sotmès un material poden alterar aquesta microestructura. La varietat de mecanismes d'enfortiment que alteren la resistència d'un material inclou enduriment per treball, enfortiment de la solució sòlida, enduriment per precipitació i enfortiment del límit del gra i es pot explicar quantitativament i qualitativament. Els mecanismes d'enfortiment van acompanyats de l'advertència que algunes altres propietats mecàniques del material poden degenerar en un intent de fer-lo més fort. Per exemple, en l'enfortiment del límit del gra, encara que la resistència de fluència es maximitza amb la disminució de la mida del gra, en última instància, les mides de gra molt petites fan que el material sigui trencadís. En general, el límit elàstic d'un material és un indicador adequat de la resistència mecànica del material. Considerat conjuntament amb el fet que el límit elàstic és el paràmetre que prediu la deformació plàstica en el material, es poden prendre decisions informades sobre com augmentar la resistència d'un material en funció de les seves propietats microestructurals i de l'efecte final desitjat. La resistència s'expressa en termes dels valors límit de la tensió de compressió, tensió de tracció i esforç de tall que causarien fallades. Els efectes de la càrrega dinàmica són probablement la consideració pràctica més important de la resistència dels materials, especialment el problema de la fatiga. La càrrega repetida sovint inicia esquerdes fràgils, que creixen fins que es produeix una fallada. Les esquerdes comencen sempre en una concentració de tensió, especialment canvis en la secció transversal de l'objecte, prop de forats i cantonades a nivells de tensió nominal molt inferiors als indicats per a la resistència del material.

Referències

1. Beer i Johnston, 2001, p. 210.
2. Beer i Johnston, 2001, p. 7.
3. Beer i Johnston, 2001, p. 5.
4. Beer i Johnston, 2001, p. 9–10.
5. Beer i Johnston, 2001, p. 52.
6. Beer i Johnston, 2001, p. 60.
7. Beer i Johnston, 2001, p. 47.
8. Beer i Johnston, 2001, p. 49.
9. Beer i Johnston, 2001, p. 305.
10. Beer i Johnston, 2001, p. 53–56.
11. Beer i Johnston, 2001, p. 27–28.
12. Beer i Johnston, 2001, p. 28.

Vegeu també

• Corba tensió-deformació

Bibliografia

• Beer, F.P.; Johnston, E.R.. Mechanics of Materials. 3a. McGraw-Hill, 2001. ISBN 0-07-248673-2.
• Den Hartog, Jacob P., Strength of Materials, Dover Publications, Inc., 1961, ISBN 0-486-60755-0
• Popov, Egor P., Engineering Mechanics of Solids, Prentice Hall, Englewood Cliffs, N. J., 1990, ISBN 0-13-279258-3
• Monleón Cremades, Salvador, Análisis de vigas, arcos, placas y láminas, Universitat Politècnica de València, 1999, ISBN 84-7721-769-6
• Timoshenko S., Strength of Materials, 3rd ed., Krieger Publishing Company, 1976, ISBN 0-88275-420-3