Залатое сячэнне

У паняцця ёсць і іншыя значэнні, гл. Залатое сячэнне.

Залатое сячэнне (залатая прапорцыя, дзяленне ў крайняй і сярэдняй адносіне, гарманічнае дзяленне) — адносіна дзвюх велічынь a і b, b > a, калі справядліва b/a = (a+b)/b. Лік, роўны адносіне b/a, звычайна абазначаецца грэчаскай літарай ${\displaystyle \varphi }$, радзей — грэчаскай літарай ${\displaystyle \tau }$. З зыходнай роўнасці няцяжка атрымаць, што

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}.}$

Сістэма злічэння	Ацэнка ліку φ
Двайковая	1.1001111000110111011…
Дзесятковая	1.6180339887498948482…
Шаснаццаткавая	1.9E3779B97F4A7C15F39…
Непарыўны дроб	${\displaystyle 1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}}$

1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362

---

Першыя 1000 дзесятковых знакаў ліку φ, разлічаныя камп'ютарам у 1996 годзе^[1].

Адваротны лік

${\displaystyle {\frac {1}{\varphi }}={\frac {-1+{\sqrt {5}}}{2}}.}$

Адсюль вынікае, што

${\displaystyle {\frac {1}{\varphi }}=\varphi -1.}$

Для практычных мэт абмяжоўваюцца прыблізным значэннем ${\displaystyle \varphi =1{,}618}$ ці ${\displaystyle \varphi =1{,}62}$. У працэнтным акругленым значэнні залатое сячэнне — гэта дзяленне якой-небудзь велічыні ў адносінах 62 % і 38 %.

Гістарычна першапачаткова залатым сячэннем называлася дзяленне адрэзка АВ кропкай С на дзве часткі (меншы адрэзак АС і большы адрэзак СВ), каб для даўжынь адрэзкаў было верна AC/CB = CB/AВ. Пазней гэта было распаўсюджана на адвольныя велічыні.

Лік ${\displaystyle \varphi }$ называецца таксама залатым лікам.

У дайшоўшай да нас антычнай літаратуры дзяленне адрэзка ў крайняй і сярэдняй адносіне (ἄκρος καὶ μέσος λόγος) упершыню сустракаецца ў «Пачатках» Еўкліда (каля 300 г. да н. э.), дзе яно прымяняецца для пабудовы правільнага пяцівугольніка.

Лука Пачолі, сучаснік і друг Леанарда да Вінчы, называў гэту адносіну «боскай прапорцыяй». Тэрмін «залатое сячэнне» (ням.: goldener schnitt) быў уведзены ва ўжытак Марцінам Омам ў 1835 годзе.

Залатое сячэнне мае мноства выдатных уласцівасцей, але, акрамя таго, яму прыпісваюць і многія выдуманыя ўласцівасці^[2][3][4].

Матэматычныя ўласцівасці

Адрэзаўшы квадрат ад прамавугольніка, пабудаванага па прынцыпе залатога сячэння, мы атрымліваем новы, паменшаны прамавугольнік з тымі ж адносінамі старон a/b=(a+b)/a

Лікава-алгебраічныя ўласцівасці

• ${\displaystyle \varphi }$ — ірацыянальны алгебраічны лік, дадатнае рашэнне квадратнага ўраўнення

  ${\displaystyle x^{2}-x-1=0,}$

адкуль, у прыватнасці, вынікаюць суадносіны:

${\displaystyle \varphi \cdot (\varphi -1)=1.}$

• ${\displaystyle \varphi }$ выражаецца праз значэнні трыганаметрычных функцый:

  ${\displaystyle \varphi =2\cos {\frac {\pi }{5}}=2\cos 36^{\circ }.}$

  ${\displaystyle \varphi =2\sin(3\pi /10)=2\sin 54^{\circ }.}$

• ${\displaystyle \varphi }$ прадстаўляецца ў выглядзе бесканечнага ланцужка квадратных каранёў:

  ${\displaystyle \varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}$

• ${\displaystyle \varphi \;}$ прадстаўляецца ў выглядзе бесканечнага ланцуговага дробу

  ${\displaystyle \varphi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}$

падыходнымі дробамі якой служаць адносіны паслядоўных лікаў Фібаначы ${\displaystyle {\frac {F_{n+1}}{F_{n}}}}$. Такім чынам,

${\displaystyle \varphi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}.}$

• Мера ірацыянальнасці ${\displaystyle \varphi }$ роўная 2.

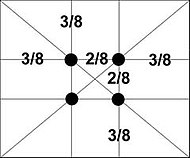
• Значэнні дробу пасля коскі для ${\displaystyle \varphi }$, ${\displaystyle {\frac {1}{\varphi }}}$ і ${\displaystyle \varphi ^{2}}$ у любой сістэме злічэння будуць роўныя^[5].

Геаметрычныя ўласцівасці

Залатое сячэнне ў пяціканцовай зорцы

Пабудова залатога сячэння

Мазаіка Пенроўза

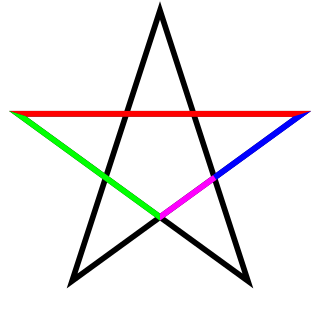
• У правільнай пяціканцовай зорцы кожны адрэзак дзеліцца перасякаючым яго адрэзкам у залатым сячэнні (на прыведзеным малюнку адносіны чырвонага адрэзка да зялёнага, зялёнага да сіняга і сіняга да пурпурнага роўныя ${\displaystyle \varphi }$. Акрамя таго, адносіна чырвонага адрэзка да адлегласці паміж суседнімі вяршынямі зоркі (якое роўна зялёнаму адрэзку), таксама роўная ${\displaystyle \varphi }$).

• Адносіна дыяганалі правільнага пяцівугольніка да стараны роўна залатому сячэнню.
• Пры дзяленні папалам вугла паміж дыяганаллю і меншай стараной прамавугольніка з адносінамі старон 1:2 атрымліваем лік

  ${\displaystyle {\frac {1}{\varphi }}=\operatorname {tg} \left({\frac {\operatorname {arctg} 2}{2}}\right).}$

Геаметрычная пабудова

Залатое сячэнне адрэзка ${\displaystyle AB}$ можна пабудаваць наступным чынам: у пункце ${\displaystyle B}$ будуюць перпендыкуляр да ${\displaystyle AB}$, адкладваюць на ім адрэзак ${\displaystyle BC}$, роўны палавіне ${\displaystyle AB}$, на адрэзку ${\displaystyle AC}$ адкладваюць адрэзак ${\displaystyle CD}$, роўны ${\displaystyle BC}$, і нарэшце, на адрэзку ${\displaystyle AB}$ адкладваюць адрэзак ${\displaystyle AE}$, роўны ${\displaystyle AD}$ . Тады

${\displaystyle \varphi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|EB|}}.}$

Залатое сячэнне і гармонія ў мастацтве

Залатое сячэнне і зрокавыя цэнтры

Пад «правілам залатога сячэння» ў архітэктуры і мастацтве звычайна маюцца на ўвазе кампазіцыі, якія змяшчаюць прапорцыі, блізкія да залатога сячэння.

Некаторыя са сцвярджэнняў на карысць гіпотэзы ведання старажытнымі правіла залатога сячэння:

• Прапорцыі піраміды Хеопса, храмаў, барэльефаў, прадметаў побыту і ўпрыгажэнняў з грабніцы Тутанхамона сведчаць, што егіпецкія майстры карысталіся суадносінамі залатога сячэння пры іх стварэнні.
• Згодна з Ле Карбюзье, у рэльефе з храма фараона Сеці I у Абідасе прапорцыі фігур адпавядаюць залатому сячэнню. У фасадзе старажытнагрэчаскага храма Парфенона таксама прысутнічаюць залатыя прапорцыі. У цыркулі з старажытнарымскага горада Пампеі (музей у Неапалі) таксама закладзены прапорцыі залатога дзялення, і т. д.
• Варта адзначыць, што сама дакладная прапорцыя з'яўляецца ідэальным эталонным значэннем. У прыродзе рэальныя суадносіны у біялагічных відаў, як правіла, трохі адрозніваюцца ад залатога сячэння, што выклікана прыстасаваннем да навакольнага асяроддзя ў працэсе жыцця. Прыкладам такіх «адхіленняў» можа служыць марская камбала.

Прыклады свядомага выкарыстання

Пачынаючы з Леанарда да Вінчы, многія мастакі свядома выкарыстоўвалі прапорцыі «залатога сячэння». Расійскі дойлід Жалтоўскі выкарыстоўваў залатое сячэнне ў сваіх праектах^[6]. Іаган Себасцьян Бах у сваёй інвенцыі E-dur № 6 BWV 792 выкарыстоўваў двухчасткавую форму, у якой суадносіны памераў частак адпавядаюць прапорцыям залатога сячэння. 1 частка — 17 тактаў, 2 частка — 24 такты. (Невялікія неадпаведнасці выраўноўваюцца за кошт ферматы ў 34 такце).

Геаметрыя плана грабніцы фараона Старажытнага Егіпта Менеса пабудавана з выкарыстаннем прапорцыі, якую мы цяпер звязваем з залатым сячэннем^[7].

Залатое сячэнне ў біялогіі і медыцыне

Залатое сячэнне ў прыродзе

Жывыя сістэмы таксама валодаюць уласцівасцямі, характэрнымі для «залатога сячэння». Напрыклад: прапорцыі цел, спіральныя структуры ці параметры біярытмаў^[8] і інш.

Гл. таксама

• Піфагарэйскі пентакл^be_ru
• Фібаначыева сістэма злічэння^be_ru
• Правіла трэцей^be_ru
• Метад залатога сячэння^be_ru

Зноскі

1. Golden ratio 1000 digits
2. Радзюкевич А. В. Красивая сказка о «золотом сечении»
3. Mario Livio, The Golden Ratio: The Story of Phi, The World's Most Astonishing Number
4. Devlin's Angle, The Myth That Will Not Go Away
5. Системы счисления (нявызн.).
6. Золотой запас зодчества Архівавана 29 студзеня 2009.
7. Стеликов Н. Е. «Гармония древнеегипетской архитектуры.» Горки: БГСХА. 2009, 108 с.
8. Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.

Літаратура

• Залатое сячэнне // Беларуская энцыклапедыя: У 18 т. Т. 6: Дадаізм — Застава / Рэдкал.: Г. П. Пашкоў і інш. — Мн. : БелЭн, 1998. — Т. 6. С. 510.
• Золотое сечение // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1979. — Т. 2. — 552 с. — 150 000 экз. Стл. 466—467.
• Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
• Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973
• Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
• Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
• Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
• Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
• Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.

Спасылкі

• В. С. Белнин, «Владел ли Платон кодом золотой пропорции? Анализ мифа» Архівавана 13 мая 2009.
• А. В. Радзюкевич, К вопросу о научном изучении пропорций в архитектуре и искусстве.
• А. В. Радзюкевич, Критический анализ Адольфа Цейзинга — основоположника гипотезы «золотого сечнения».
• В. Лаврус, Золотое сечение
• Статья о золотом сечении в изобразительном искусстве, Золотое сечение в изобразительном искусстве Архівавана 1 кастрычніка 2011.
• Функция Фибоначчи в Wolfram alpha
• Weisstein, Eric W.. Golden Ratio (нявызн.). MathWorld.

•  A001622