BA
All
Articles
Dictionary
Quotes
Map

Wikiwand ❤️ Wikipedia

PrivacyTerms

Пи (һан)

математик даими, әйләнәнең оҙонлоғоноң уның диаметрына сағыштырмаһына тигеҙ булған һан From Wikipedia, the free encyclopedia

Пи (һан)
ҮҙсәнлектәреТранцендентлыҡ һәм иррационаллекНисбәттәрТарихыГеометрик осорКлассик периодТождестволарға нигеҙләнгән ысулдарКомпьютер иҫәпләүҙәре эраһыРациональ яҡынлашыуҙарыХәл ителмәгән проблемаларБюффон энәһе ысулыМнемоник ҡағиҙәләрӨҫтәлмә факттарМәҙәниәттәШулай уҡ ҡарағыҙИҫкәрмәләрӘҙәбиәтҺылтанмалар

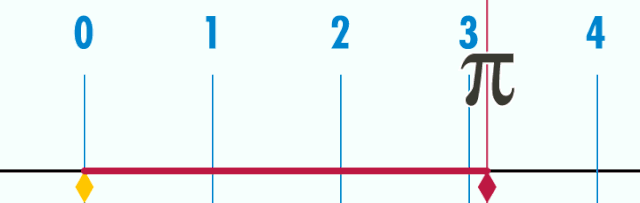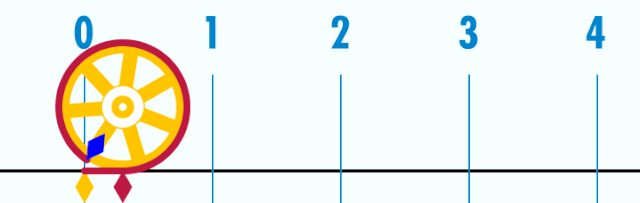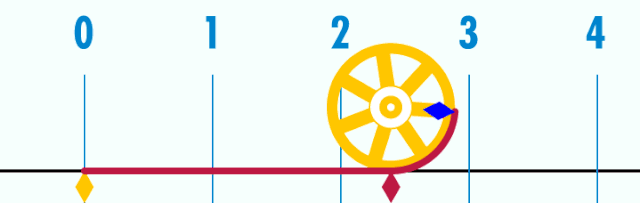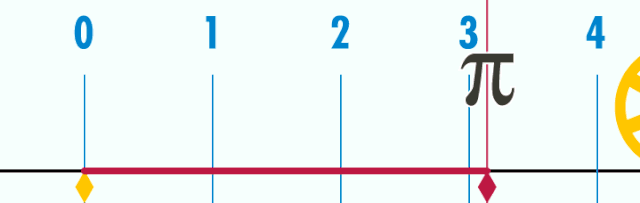
π {\displaystyle {\boldsymbol {\pi }}} {\displaystyle {\boldsymbol {\pi }}} («пи» тип әйтелә) — математик даими, әйләнәнең оҙонлоғоноң уның диаметрына сағыштырмаһына тигеҙ булған һан[K 1]. Грек алфавитының «π» хәрефе менән тамғалана.

Был терминдың башҡа мәғәнәләре лә бар, ҡарағыҙ: Пи.
Ҡыҫҡа факттар
Иррациональ һандар
ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — e π {\displaystyle e^{\pi }} {\displaystyle e^{\pi }} и π
Иҫәпләү системаһы π {\displaystyle \pi } {\displaystyle \pi } һанына баһа
Унарлы3,1415926535897932384626433832795…
Икеле11,00100100001111110110…
Ун алтылы3,243F6A8885A308D31319…
Алтмышарлы3; 08 29 44 00 47 25 53 07 …
Рациональ яҡынайыуҙар22⁄7, 179⁄57, 223⁄71, 333⁄106, 355⁄113, 103 993⁄33 102 (теүәллеге арта барыу тәртибендә һанап кителгән)
Өҙлөкһөҙ кәсер[3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, … ]

(Был өҙлөкһөҙ кәсер периодлы түгел. Һыҙыҡлы нотацияла яҙылған)

Тригонометрия π {\displaystyle \pi } {\displaystyle \pi } радиан = 180°
Ябырға

3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989
…

π {\displaystyle \pi } {\displaystyle \pi } һаны унарлы кәсерҙең тәүге мең юғары разряды менән[1]
Thumb
Әгәр әйләнәнең диаметры бергә тигеҙ булһа, әйләнәнең оҙонлоғо — ул «пи» һаны

Транцендентлыҡ һәм иррационаллек

π {\displaystyle \pi } {\displaystyle \pi } һаны иррациональ, йәғни уның ҡиммәте m n {\displaystyle {\frac {m}{n}}} {\displaystyle {\frac {m}{n}}} кәсере күренешендә теүәл күрһәтелә алмай, бында m {\displaystyle m} {\displaystyle m} һәм n {\displaystyle n} {\displaystyle n} — бөтөн һандар. Ошонан сығып, уның унарлы яҙылышы тамамланмай (сикһеҙ) һәм периодлы була алмай. π {\displaystyle \pi } {\displaystyle \pi } һанының иррационаллеген беренсе булып 1761 йылда Иоганн Ламберт[2] тангенсты өҙлөкһөҙ кәсергә тарҡатыу юлы менән иҫбатлай. 1794 йылда Лежандр π {\displaystyle \pi } {\displaystyle \pi } һәм π 2 {\displaystyle \pi ^{2}} {\displaystyle \pi ^{2}} һандарының иррационаллегенең ҡәтғиерәк иҫбатланышын килтерә.

π {\displaystyle \pi } {\displaystyle \pi } — транцендент һан, йәғни ул коэффициенттары бөтөн һандар булған ниндәй ҙә булһа тигеҙләмәнең тамыры була алмай. π {\displaystyle \pi } {\displaystyle \pi } һанының транцендентлығын 1882 йылда Кёнигсберг, ә аҙаҡ Мюнхен университеты профессоры Линдеман иҫбатлай. Иҫбатлауҙы Феликс Клейн 1894 йылда ябайлаштыра[3]. Евклид геометрияһында түңәрәктең майҙаны һәм әйләнә оҙонлоғо π {\displaystyle \pi } {\displaystyle \pi } һанының функциялары булғанлыҡтан, π {\displaystyle \pi } {\displaystyle \pi } һанының транцендентлығын иҫбатлау 2,5 мең йылдан артыҡ һуҙылған түңәрәктең квадратураһын төҙөргә маташыуҙарға сик ҡуя.

1934 йылда Гельфонд[4] e π {\displaystyle e^{\pi }} {\displaystyle e^{\pi }} һанының транцендентлығын иҫбатлай. 1996 йылда Юрий Нестеренко теләһә ниндәй натураль n {\displaystyle n} {\displaystyle n} өсөн π {\displaystyle \pi } {\displaystyle \pi } һәм e π n {\displaystyle e^{\pi {\sqrt {n}}}} {\displaystyle e^{\pi {\sqrt {n}}}} һандары алгебрак бәйләнешһеҙ икәнен иҫбатлай, бынан, айырым алғанда,[5][6] π + e π , π e π {\displaystyle \pi +e^{\pi },\pi e^{\pi }} {\displaystyle \pi +e^{\pi },\pi e^{\pi }} һәм e π n {\displaystyle e^{\pi {\sqrt {n}}}} {\displaystyle e^{\pi {\sqrt {n}}}} һандарының транцендентлығы килеп сыға.

π {\displaystyle \pi } {\displaystyle \pi } периодтар ҡулсаһының элементы булып тора (тимәк, иҫәпләнмәле һәм арифметик һан). Ләкин 1 / π {\displaystyle 1/\pi } {\displaystyle 1/\pi } периодтар ҡулсаһына инәме икәне билдәһеҙ.

Нисбәттәр

π {\displaystyle \pi } {\displaystyle \pi } һанын иҫәпләү өсөн күп формулалар билдәле:

  • π һанының яҡынлауы өсөн Виет формулаһы[en]:
2 π = 2 2 ⋅ 2 + 2 2 ⋅ 2 + 2 + 2 2 ⋅ … {\displaystyle {\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \ldots } {\displaystyle {\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \ldots }
Был π {\displaystyle \pi } {\displaystyle \pi } һанының сикһеҙ һандағы ғәмәлдәр менән тәүге билдәле асыҡ күренеше. Уны ошолай иҫбатларға мөмкин. sin ⁡ 2 φ = 2 sin ⁡ φ cos ⁡ φ {\displaystyle \sin 2\varphi =2\sin \varphi \cos \varphi } {\displaystyle \sin 2\varphi =2\sin \varphi \cos \varphi } тождествоһын рекурсив ҡулланып һәм сикләнмәгә күсеп, табабыҙ
φ cos ⁡ φ 2 cos ⁡ φ 4 ⋯ = sin ⁡ φ . {\displaystyle \varphi \cos {\dfrac {\varphi }{2}}\cos {\frac {\varphi }{4}}\cdots =\sin \varphi .} {\displaystyle \varphi \cos {\dfrac {\varphi }{2}}\cos {\frac {\varphi }{4}}\cdots =\sin \varphi .}
φ = π 2 {\displaystyle \varphi ={\frac {\pi }{2}}} {\displaystyle \varphi ={\frac {\pi }{2}}} алмаштырып ҡуяһы һәм икеләтелгән мөйөш косинусы формулаһын ҡулланаһы ҡала: cos ⁡ 2 φ = cos 2 ⁡ φ − sin 2 ⁡ φ . {\displaystyle \cos 2\varphi =\cos ^{2}\varphi -\sin ^{2}\varphi .} {\displaystyle \cos 2\varphi =\cos ^{2}\varphi -\sin ^{2}\varphi .}
  • Валлис формулаһы:
2 1 ⋅ 2 3 ⋅ 4 3 ⋅ 4 5 ⋅ 6 5 ⋅ 6 7 ⋅ 8 7 ⋅ 8 9 ⋯ = π 2 {\displaystyle {\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots ={\frac {\pi }{2}}} {\displaystyle {\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots ={\frac {\pi }{2}}}
  • Лейбниц рәте:
1 1 − 1 3 + 1 5 − 1 7 + 1 9 − ⋯ = π 4 {\displaystyle {\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-\cdots ={\frac {\pi }{4}}} {\displaystyle {\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-\cdots ={\frac {\pi }{4}}}
  • Башҡа рәттәр:
1 1 2 + 1 2 2 + 1 3 2 + 1 4 2 + 1 5 2 + ⋯ = π 2 6 {\displaystyle {\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+\dots ={\frac {\pi ^{2}}{6}}} {\displaystyle {\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+\dots ={\frac {\pi ^{2}}{6}}} (кире квадраттар рәте)
π = 1 2 ∑ k = 0 ∞ 1 16 k ( 8 8 k + 2 + 4 8 k + 3 + 4 8 k + 4 − 1 8 k + 7 ) = = 1 4 ∑ k = 0 ∞ 1 16 k ( 8 8 k + 1 + 8 8 k + 2 + 4 8 k + 3 − 2 8 k + 5 − 2 8 k + 6 − 1 8 k + 7 ) = = ∑ k = 0 ∞ ( − 1 ) k 4 k ( 2 4 k + 1 + 2 4 k + 2 + 1 4 k + 3 ) {\displaystyle {\begin{aligned}\pi &={\frac {1}{2}}\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {8}{8k+2}}+{\frac {4}{8k+3}}+{\frac {4}{8k+4}}-{\frac {1}{8k+7}}\right)=\\&={\frac {1}{4}}\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {8}{8k+1}}+{\frac {8}{8k+2}}+{\frac {4}{8k+3}}-{\frac {2}{8k+5}}-{\frac {2}{8k+6}}-{\frac {1}{8k+7}}\right)=\\&=\;\;\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{4^{k}}}\left({\frac {2}{4k+1}}+{\frac {2}{4k+2}}+{\frac {1}{4k+3}}\right)\end{aligned}}} {\displaystyle {\begin{aligned}\pi &={\frac {1}{2}}\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {8}{8k+2}}+{\frac {4}{8k+3}}+{\frac {4}{8k+4}}-{\frac {1}{8k+7}}\right)=\\&={\frac {1}{4}}\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {8}{8k+1}}+{\frac {8}{8k+2}}+{\frac {4}{8k+3}}-{\frac {2}{8k+5}}-{\frac {2}{8k+6}}-{\frac {1}{8k+7}}\right)=\\&=\;\;\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{4^{k}}}\left({\frac {2}{4k+1}}+{\frac {2}{4k+2}}+{\frac {1}{4k+3}}\right)\end{aligned}}}
π = 2 3 ∑ k = 0 ∞ ( − 1 ) k 3 k ( 2 k + 1 ) {\displaystyle \pi =2{\sqrt {3}}\sum \limits _{k=0}^{\infty }{\frac {(-1)^{k}}{\,3^{k}\,(2k+1)}}} {\displaystyle \pi =2{\sqrt {3}}\sum \limits _{k=0}^{\infty }{\frac {(-1)^{k}}{\,3^{k}\,(2k+1)}}}
  • Тапҡыр рәттәр:
π = 8 ∑ k = 1 ∞ ∑ m = 1 ∞ 1 ( 4 m − 2 ) 2 k = 4 ∑ k = 1 ∞ ∑ m = 1 ∞ m 2 − k 2 ( m 2 + k 2 ) 2 = 360 ∑ k = 1 ∞ ∑ m = 1 k 1 m ( k + 1 ) 3 4 {\displaystyle \pi =8\sum \limits _{k=1}^{\infty }\sum \limits _{m=1}^{\infty }{\frac {1}{(4m-2)^{2k}}}=4\sum \limits _{k=1}^{\infty }\sum \limits _{m=1}^{\infty }{\frac {m^{2}-k^{2}}{(m^{2}+k^{2})^{2}}}={\sqrt[{4\,\,}]{360\sum \limits _{k=1}^{\infty }\sum \limits _{m=1}^{k}{\frac {1}{m(k+1)^{3}}}}}} {\displaystyle \pi =8\sum \limits _{k=1}^{\infty }\sum \limits _{m=1}^{\infty }{\frac {1}{(4m-2)^{2k}}}=4\sum \limits _{k=1}^{\infty }\sum \limits _{m=1}^{\infty }{\frac {m^{2}-k^{2}}{(m^{2}+k^{2})^{2}}}={\sqrt[{4\,\,}]{360\sum \limits _{k=1}^{\infty }\sum \limits _{m=1}^{k}{\frac {1}{m(k+1)^{3}}}}}}
  • Сикләнмәләр:
π = lim m → ∞ ( m ! ) 4 2 4 m [ ( 2 m ) ! ] 2 m {\displaystyle \pi =\lim \limits _{m\rightarrow \infty }{\frac {(m!)^{4}\,{2}^{4m}}{\left[(2m)!\right]^{2}\,m}}} {\displaystyle \pi =\lim \limits _{m\rightarrow \infty }{\frac {(m!)^{4}\,{2}^{4m}}{\left[(2m)!\right]^{2}\,m}}}
π = 6 lim n → ∞ ∏ k = 1 p k ∈ P n ( 1 − 1 p k 2 ) → {\displaystyle \pi ={\sqrt {\frac {6}{\lim \limits _{n\to \infty }\prod \limits _{k=1 \atop p_{k}\in \mathbf {P} }^{n}\,\left(1-{\frac {1}{p_{k}^{2}}}\right)}}}\quad \to } {\displaystyle \pi ={\sqrt {\frac {6}{\lim \limits _{n\to \infty }\prod \limits _{k=1 \atop p_{k}\in \mathbf {P} }^{n}\,\left(1-{\frac {1}{p_{k}^{2}}}\right)}}}\quad \to } бында p k {\displaystyle p_{k}} {\displaystyle p_{k}} — ябай һандар
π = lim n → ∞ 2 n 2 − 2 + 2 + 2 + ⋯ + 2 , {\displaystyle \pi =\lim _{n\to \infty }2^{n}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+\dots +{\sqrt {2}}}}}}}}}},} {\displaystyle \pi =\lim _{n\to \infty }2^{n}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+\dots +{\sqrt {2}}}}}}}}}},} бында n {\displaystyle n} {\displaystyle n} аңлатманың тамырҙар һаны.[7]
  • Эйлер тождествоһы:
e i π + 1 = 0 {\displaystyle e^{i\pi }+1=0\;} {\displaystyle e^{i\pi }+1=0\;}
  • Константалар араһында башҡа бәйләнештәр:
π e = 2 ∏ k = 1 ∞ ( 2 k + 1 2 k − 1 ) 2 k − 1 ( k k + 1 ) 2 k {\displaystyle {\frac {\pi }{e}}=2\prod \limits _{k=1}^{\infty }\left({\frac {2k+1}{2k-1}}\right)^{2k-1}\left({\frac {k}{k+1}}\right)^{2k}} {\displaystyle {\frac {\pi }{e}}=2\prod \limits _{k=1}^{\infty }\left({\frac {2k+1}{2k-1}}\right)^{2k-1}\left({\frac {k}{k+1}}\right)^{2k}}
π ⋅ e = 6 ∏ k = 1 ∞ ( 2 k + 3 2 k + 1 ) 2 k + 1 ( k k + 1 ) 2 k {\displaystyle \pi \cdot e=6\prod \limits _{k=1}^{\infty }\left({\frac {2k+3}{2k+1}}\right)^{2k+1}\left({\frac {k}{k+1}}\right)^{2k}} {\displaystyle \pi \cdot e=6\prod \limits _{k=1}^{\infty }\left({\frac {2k+3}{2k+1}}\right)^{2k+1}\left({\frac {k}{k+1}}\right)^{2k}}
  • Пуассон интегралы йәки Гаусс интегралы
∫ − ∞ + ∞   e − x 2 d x = π {\displaystyle \int \limits _{-\infty }^{+\infty }\ e^{-x^{2}}{dx}={\sqrt {\pi }}} {\displaystyle \int \limits _{-\infty }^{+\infty }\ e^{-x^{2}}{dx}={\sqrt {\pi }}}
∫ 0 ∞ B r ( x ) e B r 4 ( x ) d x = π , {\displaystyle \int \limits _{0}^{\infty }{\frac {Br(x)}{\displaystyle e^{Br^{4}(x)}}}dx={\sqrt {\pi }},} {\displaystyle \int \limits _{0}^{\infty }{\frac {Br(x)}{\displaystyle e^{Br^{4}(x)}}}dx={\sqrt {\pi }},} где B r ( x ) {\displaystyle Br(x)} {\displaystyle Br(x)} — Бринг тамыры.
  • Интеграл синусы:
∫ − ∞ + ∞ sin ⁡ x x d x = π {\displaystyle \int \limits _{-\infty }^{+\infty }{{\frac {\sin x}{x}}dx}=\pi } {\displaystyle \int \limits _{-\infty }^{+\infty }{{\frac {\sin x}{x}}dx}=\pi }
  • Дилогарифм аша күрһәтеү:[8]
π = 6 ln 2 ⁡ 2 + 12   Li 2 ⁡ ( 1 2 ) {\displaystyle \pi ={\sqrt {6\ln ^{2}2+12\ \operatorname {Li} _{2}\left({\frac {1}{2}}\right)}}} {\displaystyle \pi ={\sqrt {6\ln ^{2}2+12\ \operatorname {Li} _{2}\left({\frac {1}{2}}\right)}}}
  • Үҙ булмаған интеграл аша
∫ 0 + ∞ d x ( x + 1 ) x = π {\displaystyle \int \limits _{0}^{+\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi } {\displaystyle \int \limits _{0}^{+\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi }
Thumb
константа символы

Был һандың грек хәрефе π {\displaystyle \pi } {\displaystyle \pi } менән тамғаланышын беренсе булып 1706 йылда Британия математигы Джонс файҙаланған[9], ә Леонард Эйлерҙың 1737 йылдағы хеҙмәттәренән һуң ул дөйөм ҡабул ителә. Был тамғалау περιφέρεια әйләнә, периферия һәм περίμετρος периметр тигән грек һүҙҙәренең баш хәрефенән алынған [10].

π {\displaystyle \pi } {\displaystyle \pi } һанын өйрәнеү һәм уның ҡиммәтен аныҡлау бөтә математиканың үҫеше менән параллель бара һәм бер нисә мең йыллыҡты алып тора. Тәүҙә π {\displaystyle \pi } {\displaystyle \pi } геометрия ҡарашынан сығып өйрәнелә, аҙаҡ математик анализдың XVII быуатта үҫеше был һандың универсаль булыуын күрһәтә.

Геометрик осор

Әйләнәнең оҙонлоғоноң диаметрға сағыштырмаһы теләһә ниндәй әйләнә өсөн дә бер төрлө булыуы, һәм был сағыштырма 3-тән бер аҙ ҙур булыуы, Боронғо Мысыр, Вавилон, Боронғо Һиндостан һәм Боронғо Греция геометрҙарына ла билдәле була, иң боронғо яҡынайыуҙары б. э. тиклем өсөнсө мең йыллыҡҡа ҡарай.

Боронғо Вавилонда π {\displaystyle \pi } {\displaystyle \pi } һанын өскә тигеҙ итеп алғандар. Уны [11] түбәндәге формула аша асыҡлағандар: түңәрәктең майҙаны әйләнә оҙонлоғоноң квадратының 12-гә бүлендегенә тигеҙ. Билдәле булған иң теүәл яҡынайыуҙарының иң тәүгеләре яҡынса б. э. тиклем 1900-сө йылдар менән даталана: был 25/8 = 3,125 (Боронғо Вавилон батшалығы осорондағы Суза балсыҡ табличкаһы)[12] һәм 256/81 ≈ 3,16 (Урта батшалыҡ осорондағы мысыр Ахмес папирусы); ике ҡиммәттең дә ысын ҡиммәтенән айырмаһы 1 %-тан ҙур түгел. Ведалар тексы «Шатапатха-брахмана» π {\displaystyle \pi } {\displaystyle \pi } һанының яҡынайыуы сифатында 339/108 ≈ 3,139 кәсерен бирә.

Ҡытай философы һәм ғалимы Чжан Хэн, II быуатта, π {\displaystyle \pi } {\displaystyle \pi } һаны өсөн ике эквивалент тәҡдим итә: 92/29 ≈ 3,1724 һәм 10 {\displaystyle {\sqrt {10}}} {\displaystyle {\sqrt {10}}} ≈ 3,1622. Джайнизмдың б. э. тиклем V—VI быуаттарҙа яҙылған изге китаптарынан, ул ваҡытта Һиндостанда ла π {\displaystyle \pi } {\displaystyle \pi } һанын 10 {\displaystyle {\sqrt {10}}} {\displaystyle {\sqrt {10}}} тигеҙ итеп ҡабул итеүҙәре күренә[13]

Thumb
Thumb
π {\displaystyle \pi } {\displaystyle \pi } һанын иҫәпләү өсөн Лю Хуэй алгоритмы

Архимед, ихтимал, беренсе булып π {\displaystyle \pi } {\displaystyle \pi } һанын иҫәпләү өсөн математик ысул тәҡдим иткән. Бының өсөн ул әйләнәгә төҙөк күпмөйөштәр ҡамаған һәм уның тирәләй ҡамаусы төҙөк күпмөйөштәр төҙөгән. Әйләнәнең диаметрын берәмек итеп алып, Архимед ҡамалған күпмөйөштөң периметрын әйләнә оҙонлоғоноң түбәнге баһаһы, ә ҡамаусы күпмөйөш периметрын юғары баһаһы итеп ҡараған. Төҙөк 96-мөйөш ҡарап, Архимед 3 10 71 < π < 3 1 7 {\displaystyle 3{\frac {10}{71}}<\pi <3{\frac {1}{7}}} {\displaystyle 3{\frac {10}{71}}<\pi <3{\frac {1}{7}}} баһаһын тапҡан һәм π {\displaystyle \pi } {\displaystyle \pi } һанын яҡынса иҫәпләү өсөн табылған сиктәрҙең юғарыһын тәҡдим иткән: — 22/7 ≈ 3,142857142857143.

Европа мәҙәниәтендә артабанғы яҡынайыу астроном Клавдий Птолемей менән бәйле (яҡынса 100 — яҡынса 170), ул ярты градус аҙымы менән хордалар таблицаһын төҙөгән, был уға π {\displaystyle \pi } {\displaystyle \pi } өсөн 377/120 яҡынлауын табырға мөмкинлек бирә, ул яҡынса Птолемей иҫәпләгән берәмек әйләнәгә ҡамалған 720-мөйөш периметрының яртыһына тигеҙ була[14]. Леонардо Пизанский (Фибоначчи) «Practica Geometriae» китабында (яҡынса 1220 й.), күрәһең, Птолемейҙың яҡынлауын π {\displaystyle \pi } {\displaystyle \pi } өсөн түбәнге сик тип уйлап, үҙенең яҡынлауын килтерә[15] — 864/275. Ләкин ул Птолемейҙыҡына ҡарағанда хөртөрәк була, сөнки Фибоначчи ярты градуслы хорданың оҙонлоғон тапҡанда ҙурыраҡ яҡҡа яңылыша, һөҙөмтәлә 377/120 яҡынлауы π {\displaystyle \pi } {\displaystyle \pi } өсөн юғары сик булып сыға.

Һиндостанда Ариабхата һәм Бхаскара 3,1416 яҡынлауын ҡулланғандар. Варахамихира VI быуатта «Панча-сиддхантика»ла 10 {\displaystyle {\sqrt {10}}} {\displaystyle {\sqrt {10}}} яҡынлауын ҡуллана.

Б. э. 265 йылында, Вэй батшалығынан математик Лю Хуэй π {\displaystyle \pi } {\displaystyle \pi } һанын теләһә ниндәй дәрәжәлә теүәллек менән иҫәпләү өсөн ябай һәм теүәл Ҡалып:Translation2 тәҡдим итә. Ул үҙ аллы 3072-мөйөш өсөн иҫәпләү яһай һәм π {\displaystyle \pi } {\displaystyle \pi } өсөн түбәндәге принцип буйынса яҡынса ҡиммәт таба:

π ≈ A 3072 = 3 ⋅ 2 8 ⋅ 2 − 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 1 ≈ 3 , 14159. {\displaystyle \pi \approx A_{3072}={3\cdot 2^{8}\cdot {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+1}}}}}}}}}}}}}}}}}}}\approx 3,14159.} {\displaystyle \pi \approx A_{3072}={3\cdot 2^{8}\cdot {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+1}}}}}}}}}}}}}}}}}}}\approx 3,14159.}

Һуңғараҡ Лю Хуэй π {\displaystyle \pi } {\displaystyle \pi } һанын тиҙ иҫәпләү ысулын уйлап таба һәм тик 96-мөйөш ярҙамында 3,1416 яҡынса ҡиммәтен таба, ул бер бер артлы килгән күпмөйөштәрҙең майҙандарының айырмаһы знаменателе 4-кә тигеҙ булған геометрик прогрессия төҙөй тигән факттың өҫтөнлөгөн ҡулланған.

480-се йылдарҙа ҡытай математигы Цзу Чунчжи π {\displaystyle \pi } {\displaystyle \pi } ≈ 355/113 булыуын күрһәткән, һәм 12288-мөйөшкә ҡарата ҡулланылған Лю Хуэй алгоритмын файҙаланып 3,1415926 < π {\displaystyle \pi } {\displaystyle \pi } < 3,1415927 икәнен күрһәткән. Был ҡиммәт артабанғы 900 йыл дауамында π {\displaystyle \pi } {\displaystyle \pi } һанының иң теүәл яҡынлауы булып ҡалған.

Классик период

II меңйыллыҡҡа тиклем π {\displaystyle \pi } {\displaystyle \pi } һанының 10-дан артыҡ булмаған цифры билдәле була. π {\displaystyle \pi } {\displaystyle \pi } һанын өйрәнеүҙә артабанғы ҙур уңыштар математик анализ үҫеше, бигерәк тә, рәттең яраҡлы һандағы быуындарын ҡушып, π {\displaystyle \pi } {\displaystyle \pi } һанын теләһә ниндәй теүәллек менән иҫәпләргә мөмкинлек биреүсе рәттәрҙе асыу менән бәйле.

Мадхава — Лейбниц рәте

1400-се йылдарҙа Сангамаграманан Мадхава шундай рәттәрҙең береһен таба:

π = 4 1 − 4 3 + 4 5 − 4 7 + ⋯ {\displaystyle {\pi }={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+\cdots } {\displaystyle {\pi }={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+\cdots }

Был һөҙөмтә Мадхава — Лейбниц рәте, йәки Грегори — Лейбниц рәте (ул өр яңынан Джеймс Грегори һәм Готфрид Лейбниц тарафынан XVII быуатта табылғандан һуң) булараҡ билдәле. Ләкин был рәт π {\displaystyle \pi } {\displaystyle \pi } һанына бик яй йыйылыусан, был практикала һандың күп цифрҙарын иҫәпләүҙең ҡатмарлылығына килтерә — Архимед баһаһын яҡшыртыу өсөн яҡынса рәттең 4000 быуынын ҡушырға кәрәк. Әммә Мадхава был рәтте

π = 12 ( 1 − 1 3 ⋅ 3 + 1 5 ⋅ 3 2 − 1 7 ⋅ 3 3 + ⋯ ) {\displaystyle \pi ={\sqrt {12}}\,\left(1-{\frac {1}{3\cdot 3}}+{\frac {1}{5\cdot 3^{2}}}-{\frac {1}{7\cdot 3^{3}}}+\cdots \right)} {\displaystyle \pi ={\sqrt {12}}\,\left(1-{\frac {1}{3\cdot 3}}+{\frac {1}{5\cdot 3^{2}}}-{\frac {1}{7\cdot 3^{3}}}+\cdots \right)}

рәтенә үҙгәртеп, һандың яҙылышында 11 цифрын дөрөҫ табып, π {\displaystyle \pi } {\displaystyle \pi }-не 3,14159265359 тип иҫәпләй алған. Был рекорд 1424 йылда фарсы математигы Джамшид әл-Каши тарафынан еңелә, ул үҙенең «Трактат об окружности» исемле хеҙмәтендә π {\displaystyle \pi } {\displaystyle \pi } һанының 17 цифрын килтерә, шуларҙың 16-һы дөрөҫ була.

Лудольф һаны

Архимед заманынан һуң Европаның беренсе индергән иң ҙур өлөшө голланд математигы Людольф ван Цейлендың өлөшө була, ул π {\displaystyle \pi } {\displaystyle \pi } һанын 20 унарлы цифры менән иҫәпләү өсөн ун йыл сарыф итә (был һөҙөмтә 1596 йылда баҫылып сыға). Архимед ысулын ҡулланып, ул икеләтеүҙе n-мөйөшкә тиклем еткерә, бында n = 60·229. Үҙенең һөҙөмтәләрен «Об окружности» китабында яҙып («Van den Circkel»), Лудольф уны ошо һүҙҙәр менән тамамлай: «Кемдең теләге бар, артабан дауам итһен әйҙә». Вафат булғандан һуң уның ҡулъяҙмаларында π {\displaystyle \pi } {\displaystyle \pi } һанының тағы ла 15 теүәл цифры асыҡланғаны беленә. Лудольф үҙе тапҡан тамғалар уның ҡәбер өҫтөнә ҡуйылған ташына уйып яҙылһын тип васыят әйтә. Уның хөрмәтенә π {\displaystyle \pi } {\displaystyle \pi } һанын ҡайһы берҙә «лудольф һаны» йәки «Лудольф константаһы» тип атайҙар.

Лудольф һаны — π {\displaystyle \pi } {\displaystyle \pi } һанының 32 дөрөҫ унарлы тамғаһы менән яҡынса ҡиммәте.

π яҡынайыуы өсөн Виет формулаһы

Сама менән шул уҡ ваҡытта Европала сикһеҙ рәттәрҙе анализлау һәм билдәләү ысулдары үҫешә башлай. Шундай тәүге тәҡдим Франсуа Виет тарафынан 1593 йылда табылған, π һанының яҡынайыуы өсөн Виет формулаһы[en] була:

2 π = 2 2 ⋅ 2 + 2 2 ⋅ 2 + 2 + 2 2 ⋅ ⋯ {\displaystyle {\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \cdots } {\displaystyle {\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \cdots }.


Валлис формулаһы

Валлис формулаһы икенсе билдәле һөҙөмтә була:

π 2 = 2 1 ⋅ 2 3 ⋅ 4 3 ⋅ 4 5 ⋅ 6 5 ⋅ 6 7 ⋅ 8 7 ⋅ 8 9 ⋯ {\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots } {\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots },

ул Джон Валлис тарафынан 1655 йылда сығарыла.

Оҡшаш ҡабатландыҡтар:

π = 3 ⋅ 3 2 ∏ k = 1 ∞ k 2 k 2 − ( 1 3 ) 2 {\displaystyle \pi =3\cdot {\frac {\sqrt {3}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {1}{3}}\right)^{2}}}} {\displaystyle \pi =3\cdot {\frac {\sqrt {3}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {1}{3}}\right)^{2}}}}

π = 3 2 ⋅ 3 2 ∏ k = 1 ∞ k 2 k 2 − ( 2 3 ) 2 {\displaystyle \pi ={\frac {3}{2}}\cdot {\frac {\sqrt {3}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {2}{3}}\right)^{2}}}} {\displaystyle \pi ={\frac {3}{2}}\cdot {\frac {\sqrt {3}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {2}{3}}\right)^{2}}}}

π = 4 ⋅ 2 2 ∏ k = 1 ∞ k 2 k 2 − ( 1 4 ) 2 {\displaystyle \pi =4\cdot {\frac {\sqrt {2}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {1}{4}}\right)^{2}}}} {\displaystyle \pi =4\cdot {\frac {\sqrt {2}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {1}{4}}\right)^{2}}}}

π = 4 3 ⋅ 2 2 ∏ k = 1 ∞ k 2 k 2 − ( 3 4 ) 2 {\displaystyle \pi ={\frac {4}{3}}\cdot {\frac {\sqrt {2}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {3}{4}}\right)^{2}}}} {\displaystyle \pi ={\frac {4}{3}}\cdot {\frac {\sqrt {2}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {3}{4}}\right)^{2}}}}

π = 6 ⋅ 1 2 ∏ k = 1 ∞ k 2 k 2 − ( 1 6 ) 2 {\displaystyle \pi =6\cdot {\frac {1}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {1}{6}}\right)^{2}}}} {\displaystyle \pi =6\cdot {\frac {1}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {1}{6}}\right)^{2}}}}

π = 6 5 ⋅ 1 2 ∏ k = 1 ∞ k 2 k 2 − ( 5 6 ) 2 {\displaystyle \pi ={\frac {6}{5}}\cdot {\frac {1}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {5}{6}}\right)^{2}}}} {\displaystyle \pi ={\frac {6}{5}}\cdot {\frac {1}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-\left({\frac {5}{6}}\right)^{2}}}}

π = 4 ⋅ ∏ k = 1 ∞ k 2 + k k 2 + k + 1 4 {\displaystyle \pi =4\cdot \prod \limits _{k=1}^{\infty }{\frac {k^{2}+k}{k^{2}+k+{\frac {1}{4}}}}} {\displaystyle \pi =4\cdot \prod \limits _{k=1}^{\infty }{\frac {k^{2}+k}{k^{2}+k+{\frac {1}{4}}}}}

π = 9 2 ⋅ 3 2 ∏ k = 1 ∞ k 2 + k k 2 + k + 2 9 {\displaystyle \pi ={\frac {9}{2}}\cdot {\frac {\sqrt {3}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}+k}{k^{2}+k+{\frac {2}{9}}}}} {\displaystyle \pi ={\frac {9}{2}}\cdot {\frac {\sqrt {3}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}+k}{k^{2}+k+{\frac {2}{9}}}}}

π = 16 3 ⋅ 2 2 ∏ k = 1 ∞ k 2 + k k 2 + k + 3 16 {\displaystyle \pi ={\frac {16}{3}}\cdot {\frac {\sqrt {2}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}+k}{k^{2}+k+{\frac {3}{16}}}}} {\displaystyle \pi ={\frac {16}{3}}\cdot {\frac {\sqrt {2}}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}+k}{k^{2}+k+{\frac {3}{16}}}}}

π = 36 5 ⋅ 1 2 ∏ k = 1 ∞ k 2 + k k 2 + k + 5 36 {\displaystyle \pi ={\frac {36}{5}}\cdot {\frac {1}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}+k}{k^{2}+k+{\frac {5}{36}}}}} {\displaystyle \pi ={\frac {36}{5}}\cdot {\frac {1}{2}}\prod \limits _{k=1}^{\infty }{\frac {k^{2}+k}{k^{2}+k+{\frac {5}{36}}}}}

Эйлер һаны e менән туғандашлыҡ бәйләнешен иҫбатлаусы ҡабатландыҡ

π = 2 3 ∏ k = 1 ∞ ( 2 k − 1 ) 1 2 − k ( 2 k + 3 ) k + 1 2 2 k + 1 ( k k + 1 ) 2 k {\displaystyle \pi =2{\sqrt {3}}\prod \limits _{k=1}^{\infty }{\frac {\left(2k-1\right)^{{\frac {1}{2}}-k}\left(2k+3\right)^{k+{\frac {1}{2}}}}{2k+1}}\left({\frac {k}{k+1}}\right)^{2k}} {\displaystyle \pi =2{\sqrt {3}}\prod \limits _{k=1}^{\infty }{\frac {\left(2k-1\right)^{{\frac {1}{2}}-k}\left(2k+3\right)^{k+{\frac {1}{2}}}}{2k+1}}\left({\frac {k}{k+1}}\right)^{2k}}

Тождестволарға нигеҙләнгән ысулдар

Яңы осорҙа π {\displaystyle \pi } {\displaystyle \pi } һанын иҫәпләү өсөн тождестволарға нигеҙләнгән аналитик ысулдар ҡулланыла. Юғарыла һанап кителгән формулалар иҫәпләү маҡсатында бик ҡулай түгелдәр, сөнки йә яй йыйылыусан рәттәрҙе ҡулланалар, йәки ҡатмарлы квадрат тамыр алыуҙы талап итәләр.

Мэчин формулалары

π һанын (шулай уҡ натураль логарифмдарҙы һәм башҡа функцияларҙы) табыуҙың үҙе үҫтергән рәттәр теорияһына һәм математик анализаға нигеҙләнгән беренсе нәтижәле һәм заманса ысулын, a r c t g 1 2 {\displaystyle \mathrm {arctg} {\frac {1}{2}}} {\displaystyle \mathrm {arctg} {\frac {1}{2}}}-ҙе рәткә тарҡатып, 1676 йылда Исаак Ньютон Ольденбургҡа икенсе хатында бирә[16]. Был ысул нигеҙендә тағы ла нәтижәлерәк формуланы 1706 йылда Джон Мэчин (John Machin) таба

π 4 = 4 a r c t g 1 5 − a r c t g 1 239 {\displaystyle {\frac {\pi }{4}}=4\,\mathrm {arctg} {\frac {1}{5}}-\mathrm {arctg} {\frac {1}{239}}} {\displaystyle {\frac {\pi }{4}}=4\,\mathrm {arctg} {\frac {1}{5}}-\mathrm {arctg} {\frac {1}{239}}}

Арктангенсты Тейлор рәтенә тарҡатып

a r c t g   x = x − x 3 3 + x 5 5 − x 7 7 + ⋯ {\displaystyle \mathrm {arctg} \ x=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots } {\displaystyle \mathrm {arctg} \ x=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots },

π {\displaystyle \pi } {\displaystyle \pi } һанын ҙурыраҡ теүәллек менән иҫәпләргә яраҡлы тиҙ йыйылыусан рәт алырға мөмкин.

Бындай типтағы формулалар хәҙерге ваҡытта Мэчин формулалары булараҡ билдәлеләр, бер нисә бер-бер артлы рекордтар ҡуйыу өсөн файҙаланылалар һәм компьютер дәүерендә π {\displaystyle \pi } {\displaystyle \pi } һанын тиҙ иҫәпләү өсөн билдәле булған ысулдарҙың иң яҡшылары булып ҡалалар. Иоганн Дазеның (en.Johann Dase) феноменаль счётчигы менән ҙур рекорд ҡуйыла, ул 1844 йылда Гаусс күрһәтмәһе буйынса Мэчин формулаһын π {\displaystyle \pi } {\displaystyle \pi } һанының 200 цифрын иҫәпләү өсөн ҡуллана [сығанаҡ 3484  көн күрһәтелмәгән]. XIX быуат аҙағына иң яҡшы һөҙөмтә инглиз Уильям Шенкс тарафынан алына, уның 707 цифрҙы иҫәпләү өсөн 15 йылы сарыф ителә, хаталаныу арҡаһында тәүге 527 цифры ғына дөрөҫ була. Шундай хаталарҙан ҡотолоу өсөн, ундай төрҙәге хәҙерге иҫәпләүҙәр ике тапҡыр башҡарылалар. Әгәр һөҙөмтәләр тап килһә, улар юғары ихтималлыҡ менән дөрөҫ булалар. Шенкстың хатаһын 1948 йылда тәүге компьютерҙарҙың береһе асыҡлай; ул үҙе бер нисә сәғәт эсендә π {\displaystyle \pi } {\displaystyle \pi } һанының 808 тамғаһын иҫәпләй.

Пи — трансцендент һан

XVIII быуатта теоретик ҡаҙаныштар π {\displaystyle \pi } {\displaystyle \pi } һанының асылына төшөнөүгә килтерә, быға тик һанлы иҫәпләүҙәр ярҙамында ғына өлгәшеү мөмкин булмаҫ ине. Иоганн Генрих Ламберт 1761 йылда π {\displaystyle \pi } {\displaystyle \pi } һанының иррационаллеген иҫбатлай, ә Адриен Мари Лежандр 1774 йылда π 2 {\displaystyle \pi ^{2}} {\displaystyle \pi ^{2}} һанының иррационаллеген иҫбатлай. 1735 йылда, Леонард Эйлер билдәле Базель проблемаһын — π 2 6 {\displaystyle {\frac {\pi ^{2}}{6}}} {\displaystyle {\frac {\pi ^{2}}{6}}} тигеҙ булып сыҡҡан

1 1 2 + 1 2 2 + 1 3 2 + 1 4 2 + ⋯ {\displaystyle {\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots } {\displaystyle {\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots } суммаһының теүәл ҡиммәтен табыу проблемаһын хәл иткәс, ябай һандар һәм π {\displaystyle \pi } {\displaystyle \pi } араһында бәйләнеш урынлаштырыла.

Лежандр ҙа, Эйлер ҙа π {\displaystyle \pi } {\displaystyle \pi } трансцендент булырға мөмкин тип фаразлайҙар, был аҙаҡҡы сиктә 1882 йылда Фердинанд фон Линдеман тарафынан иҫбат ителә.

Символ « π {\displaystyle \pi } {\displaystyle \pi }»
Төп мәҡәлә: Математик тамғалауҙар тарихы

Уильям Джонстың «Обозрение достижений математики» китабы (Synopsis Palmoriorum Mathesios, 1706 йыл) беренсе булып был константаны тамғалау өсөн грек хәрефе π {\displaystyle \pi } {\displaystyle \pi }-ны ҡулланыуға индергән тип иҫәпләнә, ләкин был тамғалау Леонард Эйлер 1737 йылда уны ҡабул иткәс (йәки бәйһеҙ рәүештә үҙе уға килгәс) дөйөм танылыу ала[10]. Эйлер былай тип яҙа: «Практиканы һиҙелерлек еңелләштерергә мөмкинлек биргән ярашлы кәкренең оҙонлоғон йәки яҫы фигураның майҙанын табыу өсөн күп башҡа ысулдар бар; мәҫәлән, түңәрәктә диаметр әйләнәнең оҙонлоғона 1 ( 16 5 − 4 239 ) − 1 3 ⋅ ( 16 5 3 − 4 239 3 ) + ⋯ = 3,141 59 ⋯ = π {\displaystyle \left({\frac {16}{5}}-{\frac {4}{239}}\right)-{\frac {1}{3}}\cdot \left({\frac {16}{5^{3}}}-{\frac {4}{239^{3}}}\right)+\cdots =3{,}14159\cdots =\pi } {\displaystyle \left({\frac {16}{5}}-{\frac {4}{239}}\right)-{\frac {1}{3}}\cdot \left({\frac {16}{5^{3}}}-{\frac {4}{239^{3}}}\right)+\cdots =3{,}14159\cdots =\pi }-гә сағыштырылған кеүек сағыштырыла».

Компьютер иҫәпләүҙәре эраһы

Цифрлы техника дәүере XX быуатта иҫәпләү рекордтарының барлыҡҡа килеү тиҙлеген арттырыуға килтерҙе. Джон фон Нейман һәм башҡалар 1949 йылда ЭНИАК-ты π {\displaystyle \pi } {\displaystyle \pi } һанының 2037 тамғаһын иҫәпләү өсөн ҡулланалар, был 70 сәғәт ваҡытты ала. 1961 йылда Дэниел Шенкс IBM 7090-да 100000 тамғаны иҫәпләй, ә миллион билдәһен 1973 йылда үтеп кителә[K 2]. Бындай прогресс аппарат менән тиҙ тәьмин итеү арҡаһында ғына түгел, ә яңы алгоритмдар арҡаһында ла мөмкин була.

XX быуат башында һинд математигы Сриниваса Рамануджан π {\displaystyle \pi } {\displaystyle \pi } өсөн бик күп яңы формулалар таба, уларҙың ҡайһы берҙәре үҙҙәренең элегантлығы һәм математик тәрәнлеге арҡаһында билдәле булып китәләр. Был формулаларҙың береһе — рәт:

1 π = 2 2 9801 ∑ k = 0 ∞ ( 4 k ) ! ( 1103 + 26390 k ) ( k ! ) 4 396 4 k {\displaystyle {\frac {1}{\pi }}={\frac {2{\sqrt {2}}}{9801}}\sum _{k=0}^{\infty }{\frac {(4k)!(1103+26390k)}{(k!)^{4}396^{4k}}}} {\displaystyle {\frac {1}{\pi }}={\frac {2{\sqrt {2}}}{9801}}\sum _{k=0}^{\infty }{\frac {(4k)!(1103+26390k)}{(k!)^{4}396^{4k}}}}.

Ир туғандар Чудновскийҙар тарафынан 1987 йылда уға оҡшаш формула табыла:

1 π = 1 426880 10005 ∑ k = 0 ∞ ( 6 k ) ! ( 13591409 + 545140134 k ) ( 3 k ) ! ( k ! ) 3 ( − 640320 ) 3 k {\displaystyle {\frac {1}{\pi }}={\frac {1}{426880{\sqrt {10005}}}}\sum _{k=0}^{\infty }{\frac {(6k)!(13591409+545140134k)}{(3k)!(k!)^{3}(-640320)^{3k}}}} {\displaystyle {\frac {1}{\pi }}={\frac {1}{426880{\sqrt {10005}}}}\sum _{k=0}^{\infty }{\frac {(6k)!(13591409+545140134k)}{(3k)!(k!)^{3}(-640320)^{3k}}}},

ул рәттең һәр быуынына яҡынса 14 цифр бирә. Чудновскийҙар был формуланы 1980-се йылдар аҙағында π {\displaystyle \pi } {\displaystyle \pi } һанын иҫәпләүҙә, формула ярҙамында 1989 йылда табылған унарлы тарҡатыуҙың 1 011 196 691 цифрын да индереп, бер нисә рекорд ҡуйыу өсөн ҡулланалар.

Хәҙерге заман рекордтары ҡуйыусы суперкомпьютерҙарҙан айырмалы рәүештә, был формула персональ компьютерҙарҙа π {\displaystyle \pi } {\displaystyle \pi } һанын иҫәпләүсе программаларҙа ҡулланыла.

Эҙмә-эҙлелек, һәр артабанғы быуыны менән теүәллекте ғәҙәттә билдәле бер дәүмәлгә арттырған бер ваҡытта, шундай итератив алгоритмдар бар, улар һәр аҙымда дөрөҫ цифрҙар һанын ҡабатлайҙар, ләкин шундай һәр аҙымда юғары иҫәпләүҙәр сарыф итеүҙе талап итәләр. Был тәңгәлдә 1975 йылда ҙур алға китеш була, Ричард Брент һәм Юджин Саламин бер береһенә бәйһеҙ рәүештә Брент — Саламин алгоритымын асалар, ул тик арифметиканы ҡулланып, һәр аҙымда билдәле тамғалар һанын икеләтә[17]. Алгоритм башланғыс ҡиммәттәрҙе

a 0 = 1 b 0 = 1 2 t 0 = 1 4 p 0 = 1 {\displaystyle a_{0}=1\quad \quad \quad b_{0}={\frac {1}{\sqrt {2}}}\quad \quad \quad t_{0}={\frac {1}{4}}\quad \quad \quad p_{0}=1} {\displaystyle a_{0}=1\quad \quad \quad b_{0}={\frac {1}{\sqrt {2}}}\quad \quad \quad t_{0}={\frac {1}{4}}\quad \quad \quad p_{0}=1}

һәм итерацияларҙы ҡуйыуҙан тора:

an һәм bn етерлек яҡын булғанға тиклем

a n + 1 = a n + b n 2 b n + 1 = a n b n {\displaystyle a_{n+1}={\frac {a_{n}+b_{n}}{2}}\quad \quad \quad b_{n+1}={\sqrt {a_{n}b_{n}}}} {\displaystyle a_{n+1}={\frac {a_{n}+b_{n}}{2}}\quad \quad \quad b_{n+1}={\sqrt {a_{n}b_{n}}}}
t n + 1 = t n − p n ( a n − a n + 1 ) 2 p n + 1 = 2 p n {\displaystyle t_{n+1}=t_{n}-p_{n}(a_{n}-a_{n+1})^{2}\quad \quad \quad p_{n+1}=2p_{n}} {\displaystyle t_{n+1}=t_{n}-p_{n}(a_{n}-a_{n+1})^{2}\quad \quad \quad p_{n+1}=2p_{n}},

Ул саҡта π {\displaystyle \pi } {\displaystyle \pi } баһаһы

π ≈ ( a n + b n ) 2 4 t n {\displaystyle \pi \approx {\frac {(a_{n}+b_{n})^{2}}{4t_{n}}}} {\displaystyle \pi \approx {\frac {(a_{n}+b_{n})^{2}}{4t_{n}}}} формулаһы менән бирелә.

Был схеманы ҡулланғанда 25 итерация 45 миллион унарлы тамғаны табыу өсөн етә. Һәр аҙымда теүәллекте дүрт тапҡыр арттырыусы оҡшаш алгоритм Джонатан Боруэйн тарафынан табыла[18]. Был ысулдар ярҙамында Ясумаса Канада һәм уның төркөмө, 1980 йылдан башлап, π {\displaystyle \pi } {\displaystyle \pi } һанын иҫәпләүҙең күпселек рекордтарын ҡуялар, 1999 йылда 206 158 430 000 тамғаға тиклем. 2002 йылда Канада һәм уның төркөмө яңы рекорд ҡуя — 1 241 100 000 000 унарлы тамға.

Канаданың алдағы күпселек рекордтары Брент — Саламин алгоритымы ярҙамында ҡуйылһа ла, 2002 йылдағы иҫәпләүҙә Мэчинов тибындағы ике формула ҡулланыла, улар яйыраҡ эшләй, ләкин хәтерҙе ҡулланыуҙы киҫкен кәметәләр.

Иҫәпләү 64 быуындан торған, оператив хәтере 1 терабайт булған Hitachi суперкомпьютерында башҡарыла, ул секундына 2 триллион операция башҡарырға һәләтле була.

1997 йылда Саймон Плафф тарафынан асылған һәм ул беренсе тапҡыр баҫылып сыҡҡан мәҡәлә авторҙары буйынса аталған Бэйли — Боруэйн — Плафф формулаһы яҡын аралағы мөһим үҫеш булып тора[19]. Был формула,

π = ∑ k = 0 ∞ 1 16 k ( 4 8 k + 1 − 2 8 k + 4 − 1 8 k + 5 − 1 8 k + 6 ) , {\displaystyle \pi =\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right),} {\displaystyle \pi =\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right),}

ул π {\displaystyle \pi } {\displaystyle \pi } һанының теләһә ниндәй конкрет ун алтылы йәки икеле цифрын алдағы цифрҙарҙы иҫәпләмәйенсә табырға мөмкинлек биреүе менән иғтибарға лайыҡ[19]. 1998 йылдан 2000 йылға тиклем PiHex төркөмләнгән проект π {\displaystyle \pi } {\displaystyle \pi } һанының квадриллионынсы битын иҫәпләү өсөн ББП Фабрис Белларҙың үҙгәртелгән формулаһын ҡуллана, ул нуль булып сыға[20].

2006 йылда Саймон Плафф, PSLQ ҡулланып, матур формулалар рәте таба[21]. q = eπ булһын, ти, ул саҡта

π 24 = ∑ n = 1 ∞ 1 n ( 3 q n − 1 − 4 q 2 n − 1 + 1 q 4 n − 1 ) {\displaystyle {\frac {\pi }{24}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\left({\frac {3}{q^{n}-1}}-{\frac {4}{q^{2n}-1}}+{\frac {1}{q^{4n}-1}}\right)} {\displaystyle {\frac {\pi }{24}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\left({\frac {3}{q^{n}-1}}-{\frac {4}{q^{2n}-1}}+{\frac {1}{q^{4n}-1}}\right)}
π 3 180 = ∑ n = 1 ∞ 1 n 3 ( 4 q n − 1 − 5 q 2 n − 1 + 1 q 4 n − 1 ) {\displaystyle {\frac {\pi ^{3}}{180}}=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}\left({\frac {4}{q^{n}-1}}-{\frac {5}{q^{2n}-1}}+{\frac {1}{q^{4n}-1}}\right)} {\displaystyle {\frac {\pi ^{3}}{180}}=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}\left({\frac {4}{q^{n}-1}}-{\frac {5}{q^{2n}-1}}+{\frac {1}{q^{4n}-1}}\right)}

һәм түбәндәге күренештәге башҡалары

π k = ∑ n = 1 ∞ 1 n k ( a q n − 1 + b q 2 n − 1 + c q 4 n − 1 ) {\displaystyle \pi ^{k}=\sum _{n=1}^{\infty }{\frac {1}{n^{k}}}\left({\frac {a}{q^{n}-1}}+{\frac {b}{q^{2n}-1}}+{\frac {c}{q^{4n}-1}}\right)} {\displaystyle \pi ^{k}=\sum _{n=1}^{\infty }{\frac {1}{n^{k}}}\left({\frac {a}{q^{n}-1}}+{\frac {b}{q^{2n}-1}}+{\frac {c}{q^{4n}-1}}\right)},

бында q = eπ, k — таҡ һан, һәм a, b, c — рациональ һандар. Әгәр k — 4m + 3 күренешендә булһа, был формула айырыуса ябай күренештә була:

p π k = ∑ n = 1 ∞ 1 n k ( 2 k − 1 q n − 1 − 2 k − 1 + 1 q 2 n − 1 + 1 q 4 n − 1 ) {\displaystyle p\pi ^{k}=\sum _{n=1}^{\infty }{\frac {1}{n^{k}}}\left({\frac {2^{k-1}}{q^{n}-1}}-{\frac {2^{k-1}+1}{q^{2n}-1}}+{\frac {1}{q^{4n}-1}}\right)} {\displaystyle p\pi ^{k}=\sum _{n=1}^{\infty }{\frac {1}{n^{k}}}\left({\frac {2^{k-1}}{q^{n}-1}}-{\frac {2^{k-1}+1}{q^{2n}-1}}+{\frac {1}{q^{4n}-1}}\right)}

знаменателе — ҡабатлашыусыларға яҡшы тарҡатып булған һан булған рациональ p өсөн, формуланың ҡәтғи иҫбатланышы әлегә юҡ.

2009 йылдың авгусында Японияның Цукуба университеты ғалимдары 2 576 980 377 524 унарлы разрядтан торған эҙмә-эҙлелекте иҫәпләп сығаралар[22].

2009 йылдың 31 декабрендә француз программисы Фабрис Беллар персональ компьютерҙа 2 699 999 990 000 унарлы разрядтан торған эҙмә-эҙлелек иҫәпләй[23].

2011 йылдың 19 октябрендә Александр Йи һәм Сигэру Кондо өтөрҙән һуң 10 триллион цифр теүәллегендә эҙмә-эҙлелекте иҫәпләйҙәр[24][25].

2013 йылдың 28 декабрендә АҠШ студенты Александр Йи һәм Япония тикшеренеүсеһе Сигэру Кондо (ja|近藤茂) өтөрҙән һуң 12,1 триллион цифрға тиклем аныҡлыҡ менән эҙмә-эҙлелекте иҫәпләйҙәр[26].

Голландия математигы Брауэр XX быуаттың беренсе яртыһында, π {\displaystyle \pi } {\displaystyle \pi } һанының унарлы тарҡалмаһында 0123456789 {\displaystyle 0123456789} {\displaystyle 0123456789} эҙмә-эҙлелеген эҙләүҙе мәғәнәһеҙ мәсьәлә миҫалы сифатында килтерә — уның фекеренсә, бының өсөн кәрәк булған теүәллеккә бер ҡасан да өлгәшеп булмаясаҡ. XX быуат аҙағында был эҙмә-эҙлелек табыла, ул өтөрҙән һуң 17 387 594 880-се тамғанан башлана[27].

  • 22 7 {\displaystyle {\frac {22}{7}}} {\displaystyle {\frac {22}{7}}} — Архимед (б. э. тиклем III быуат) — боронғо грек математигы, физигы һәм инженеры;
  • 377 120 {\displaystyle {\frac {377}{120}}} {\displaystyle {\frac {377}{120}}} — Клавдий Птолемей (б. э. тиклем II быуат) һәм Ариабхата (б. э. V быуаты) — һинд астрономы һәм математигы;
  • 355 113 {\displaystyle {\frac {355}{113}}} {\displaystyle {\frac {355}{113}}} — Цзу Чунчжи (б. э. V быуаты) — ҡытай астрономы һәм математигы.
Яҡынайыуҙарҙың теүәллеген сағыштырыу
ҺанТүңәрәкләнгән ҡиммәтеТеүәллек (разрядтарҙың тап килеүенең)
π {\displaystyle \pi } {\displaystyle \pi }3,14159265…
22 7 {\displaystyle {\frac {22}{7}}} {\displaystyle {\frac {22}{7}}}3,14285714…өтөрҙән һуң 2 разряд
377 120 {\displaystyle {\frac {377}{120}}} {\displaystyle {\frac {377}{120}}}3,14166667…өтөрҙән һуң 3 разряд
355 113 {\displaystyle {\frac {355}{113}}} {\displaystyle {\frac {355}{113}}}3,14159292…өтөрҙән һуң 6 разряд
  • π {\displaystyle \pi } {\displaystyle \pi } һәм π 2 {\displaystyle \pi ^{2}} {\displaystyle \pi ^{2}} һандары өсөн теүәл иррационаллек самаһы билдәле түгел (ләкин π {\displaystyle \pi } {\displaystyle \pi } өсөн ул 7,6063-тән артмай икәнлеге билдәле)[28][29].
  • Түбәндәге һандарҙың береһе өсөн дә иррационаллек самаһы билдәле түгел: π + e , π − e , π ⋅ e , π e , π e , π 2 , ln ⁡ π , π π , e π 2 . {\displaystyle \pi +e,\pi -e,\pi \cdot e,{\frac {\pi }{e}},\pi ^{e},\pi ^{\sqrt {2}},\ln \pi ,\pi ^{\pi },e^{\pi ^{2}}.} {\displaystyle \pi +e,\pi -e,\pi \cdot e,{\frac {\pi }{e}},\pi ^{e},\pi ^{\sqrt {2}},\ln \pi ,\pi ^{\pi },e^{\pi ^{2}}.} Уларҙың береһе өсөн дә хатта, ул рациональ һан, алгебраик иррациональ йәки трансцендент һан буламы икәнлеге лә билдәле түгел. Ошонан сығып, π {\displaystyle \pi } {\displaystyle \pi } һәм e {\displaystyle e} {\displaystyle e} һандары алгебраик бәйләнешһеҙҙәрме икәне лә билдәһеҙ[5][30][31][32][33].
  • n {\displaystyle n} {\displaystyle n}-дың ниндәйҙер ыңғай бөтөн ҡиммәтендә n π {\displaystyle {^{n}\pi }} {\displaystyle {^{n}\pi }} бөтөн һан буламы икәне билдәле түгел (см. тетрация).
  • Ошоға тиклем π {\displaystyle \pi } {\displaystyle \pi } һанының нормаллеге тураһында бер нәмә лә билдәле түгел; хатта 0—9 цифрҙарының ҡайһылары π {\displaystyle \pi } {\displaystyle \pi } һанының унарлы яҙылышында сикһеҙ һанда осрай икәне лә билдәһеҙ. π {\displaystyle \pi } {\displaystyle \pi } һанының 200 млрд унарлы тамғаһын компьютер тикшереүе күрһәтеүенсә бөтә 10 цифр был яҙылышта берҙәй йыш ҡабатлана[34]:
Ентеклерәк мәғлүмәт Цифр, Нисә тапҡыр осрай ...
ЦифрНисә тапҡыр осрай
020 000 030 841
119 999 914 711
220 000 013 697
320 000 069 393
419 999 921 691
519 999 917 053
619 999 881 515
719 999 967 594
820 000 291 044
919 999 869 180
Ябырға

Ләкин ҡәтғи иҫбатланышы юҡ.

  • 1 π {\displaystyle {\frac {1}{\pi }}} {\displaystyle {\frac {1}{\pi }}} периодтар ҡулсаһына инәме икәне билдәһеҙ.
Төп мәҡәлә: Задача Бюффона о бросании иглы

Бер тигеҙ алыҫлыҡта ятҡан тура һыҙыҡтар менән һыҙыҡлатылған яҫылыҡҡа ирекле рәүештә оҙонлоғо күрше тура һыҙыҡтар араһындағы алыҫлыҡҡа тигеҙ булған энәне шулай итеп ташлайҙар, һәр ташлағанда энә йә тура һыҙыҡтарҙы киҫмәй, йәки берәүһен генә киҫә. Энәнең ниндәй ҙә булһа һыҙыҡ менән киҫешеүҙәре һанының дөйөм ташлауҙар һанына сағыштырмаһы, ташлауҙар һаны сикһеҙлеккә тиклем артҡанда, 2 π {\displaystyle {\frac {2}{\pi }}} {\displaystyle {\frac {2}{\pi }}} һанына яҡыная икәнен иҫбат итеп була[35]. Был энә ысулы ихтималлыҡ теорияһына нигеҙләнә һәм Монте-Карло ысулының нигеҙендә ята[36].

π һанының 8—11 тамғаһын хәтерләү өсөн шиғырҙар:

Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.

Надо только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.

Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.

Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять».

Хәтерҙә ҡалдырыуға шиғыр үлсәмен һаҡлау ярҙам итергә мөмкин:

Три, четырнадцать, пятнадцать, девять два, шесть пять, три пять
Восемь девять, семь и девять, три два, три восемь, сорок шесть
Два шесть четыре, три три восемь, три два семь девять, пять ноль два
Восемь восемь и четыре, девятнадцать, семь, один

π һанының беренсе цифрҙары һүҙҙәрҙәге хәрефтәр һаны рәүешендә шифрланған шиғырҙар бар:

Это я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду.

Учи и знай в числе известном
За цифрой цифру, как удачу примечать.

Раз у Коли и Арины
Распороли мы перины.
Белый пух летал, кружился,
Куражился, замирал,
Ублажился,
Нам же дал
Головную боль старух.
Ух, опасен пуха дух!

— Георгий Александров

Бындай шиғырҙар реформаға тиклемге орфографияла ла булғандар. Мәҫәлән, артабанғы шиғырҙы Түбәнге Новгород гимназияһы уҡытыусыһы Шенрок яҙған[37]:

Кто и шутя и скоро пожелаетъ
Пи узнать, число ужъ знаетъ.

Ҡалып:Trivia

  • 21-йәшлек һинд студенты Раджвир Мина (Rajveer Meena) π {\displaystyle \pi } {\displaystyle \pi } һанының өтөрҙән һуңғы тамғаларын хәтерҙә ҡалдырыу буйынса донъя рекорды ҡуя, ул 2015 йылдың мартында 9 сәғәт 27 минут эсендә өтөрҙән һуң 70 000 тамғаны хәтергә төшөрә.[38] Быға тиклем, 10 йыл дауамында тиерлек, рекорд ҡытайлы Лю Чаола һаҡлана, ул 2006 йылда 24 сәғәт 4 минут эсендә өтөрҙән һуң 67 890 тамғаны хатаһыҙ әйтеп бирә[39][40]. Шул уҡ 2006 йылда Япониянан Акира Харагути π {\displaystyle \pi } {\displaystyle \pi } һанын өтөрҙән һуң 100-тамғаға тиклем иҫтә ҡалдырҙым тип белдерә[41], ләкин быны рәсми рәүештә тикшереү килеп сыҡмай[42]. Рәсәйҙә хәтерҙә ҡалдырыу буйынса Денис Бабушкин рекорд ҡуя (13 202 тамға)[43].
  • 1897 йылда Индиана штатында (АҠШ) пи һаны тураһында билль баҫылып сыға, ул закон менән уның ҡиммәтен 3,2-гә тигеҙ тип билдәләй[44]. Был билль, был законды ҡараған ваҡытта штаттың закон сығарыу йыйылышында ҡатнашҡан Пердью университеты профессорының ваҡытында ҡыҫылыуы арҡаһында, закон булып китмәй.
  • 1960-сы йылдарҙа сығарылған «Кит аулаусы белешмәһендә» «Гренландия киттары өсөн Пи өскә тигеҙ» тип яҙылған[45].
  • Пи һанының бирелгән һандағы тамғаларын (32 миллионға тиклем) иҫәпләүгә сарыф ителгән ваҡытты билдәләүсе «супер Пи» программаһы компьютерҙарҙың етештереүсәнлеген (нәтижәлелек) асыҡлау өсөн ҡулланылырға мөмкин.
  • 2019 йылдың 14 мартында, пи һанының рәсми булмаған байрамын билдәләгәндә, Google компанияһы был һанды өтөрҙән һуң 31,4 триллион тамға менән күрһәтә. Һанды бындай теүәллек менән Япониянан Google хеҙмәткәре Эмма Харука-Ивао иҫәпләй алған.[46]
  • Пи һаны хөрмәтенә аталған нәфис фильм бар.
  • Йыл һайын 14 мартта рәсми булмаған байрам «пи һаны көнө» билдәләнә, ул π {\displaystyle \pi } {\displaystyle \pi } һанының яҡынса ҡиммәтенә ярашлы, даталарҙың АҠШ форматында (ай/көн) 3,14 тип яҙылған көн. Байрамды 1987 йылда Сан-Франциско физигы Ларри Шоу уйлап сығарған тип иҫәпләнә[47], ул 14 мартта теүәл 01:59 сәғәттә дата һәм ваҡыт Пи = 3,14159 һанының тәүге разрядтары менән тап килеүенә иғтибар итә.
  • 22 июль π {\displaystyle \pi } {\displaystyle \pi } һаны менән бәйле тағы ла бер дата булып тора, ул «Яҡынса Пи һаны көнө» тип атала (ингл. Pi Approximation Day), сөнки Европа даталар форматында был көн 22/7 тип яҙыла, ә был кәсерҙең ҡиммәте π {\displaystyle \pi } {\displaystyle \pi } һанының яҡынса ҡиммәте булып тора.
  • Точка Фейнмана
  • Число τ
Комментарии
  1. [K 1]
    Был билдәләмә тик Евклид геометрияһы өсөн генә яраҡлы. Башҡа геометрияларҙа әйләнәнең оҙонлоғоноң уның диаметры оҙонлоғона сағыштырмаһы ирекле булырға мөмкин. Мәҫәлән, Лобачевский геометрияһында был сағыштырма π {\displaystyle \pi } {\displaystyle \pi }-ҙән бәләкәй.
  2. [K 2]
    Беҙҙең көндәрҙә ЭВМ ярҙамында π {\displaystyle \pi } {\displaystyle \pi } һаны триллион тамғаға тиклем аныҡлыҡ менән иҫәпләнгән, был фәнни файҙаға ҡарағанда техник файҙа, сөнки ундай теүәллектең практик файҙаһы юҡ. Иҫәпләү теүәллеге ғәҙәттә компьютерҙың булған ресурстары менән сикләнә, — йышыраҡ ваҡыт менән, һирәгерәк — хәтер кимәле менән.
Примечания
  1. [1]
    PI
  2. [2]
    Lambert, Johann Heinrich. Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques, стр. 265–322.
  3. [3]
    Доказательство Клейна приложено к работе «Вопросы элементарной и высшей математики», ч. 1, вышедшей в Гёттингене в 1908 году.
  4. [4]
    Weisstein, Eric W. Постоянная Гельфонда (инг.) на сайте Wolfram MathWorld.
  5. [5]
    Weisstein, Eric W. Иррациональное число (инг.) на сайте Wolfram MathWorld.
  6. [6]
    Модулярные функции и вопросы трансцендентности
  7. [7]
    Ромер П. Новое выражение для π (рус.) // В.О.Ф.Э.М.. — 1890. — № 97. — С. 2—4.
  8. [8]
    Weisstein, Eric W. Pi Squared (инг.) на сайте Wolfram MathWorld.
  9. [9]
    Гнездовский Ю. Ю.. Введение // Справочник по тригонометрии. — Экоперспектива, 2006. — С. 3. — ISBN 985-469-141-1.
  10. [10]
    Вездесущее число «пи», 2007, с. 10—11
  11. [11]
    Кымпан, 1971
  12. [12]
    E. M. Bruins. Quelques textes mathématiques de la Mission de Suse, 1950.
  13. [13]
    Стройк. Д. Я. Краткий очерк истории математики. М., Наука, 1984, с. 47-48.
  14. [14]
    Вездесущее число «пи», 2007, с. 29
  15. [15]
    Кымпан, 1971, с. 81
  16. [16]
    Исаак Ньютон. Математические работы (в переводе и переработке Мордухай-Болтовского) / Мордухай-Болтовской (также перевод и комментарии). — Москва, Ленинград: Главное изд-во технико-теоретической литературы, 1937.
  17. [17]
    Brent, Richard (1975), Traub, J F, ed., "«Multiple-precision zero-finding methods and the complexity of elementary function evaluation»", Analytic Computational Complexity (New York: Academic Press): 151–176, <http://wwwmaths.anu.edu.au/~brent/pub/pub028.html> 2008 йыл 23 июль архивланған. (инг.)
  18. [18]
    Jonathan M Borwein. Pi: A Source Book. — Springer, 2004. — ISBN 0387205713. (инг.)
  19. [19]
    David H. Bailey, Peter B. Borwein, Simon Plouffe. On the Rapid Computation of Various Polylogarithmic Constants // Mathematics of Computation. — 1997. — В. 218. — Т. 66. — С. 903—913. (инг.)
  20. [20]
    Fabrice Bellard. A new formula to compute the nth binary digit of pi (ингл.). Дата обращения: 11 ғинуар 2010. Архивировано 21 август 2011 года.
  21. [21]
    Simon Plouffe. Indentities inspired by Ramanujan’s Notebooks (part 2) (ингл.). Дата обращения: 11 ғинуар 2010. Архивировано 21 август 2011 года. 2011 йыл 26 сентябрь архивланған.
  22. [22]
    π һанын иҫәпләү теүәллегенең яңы рекорды ҡуйыла  (билдәһеҙ). Дата обращения: 20 август 2009. Архивировано из оригинала 22 август 2009 года. 2009 йыл 22 август архивланған.
  23. [23]
    Pi Computation Record
  24. [24]
    Определено 10 триллионов цифр десятичного разложения для π  (билдәһеҙ). Дата обращения: 4 октябрь 2019. Архивировано из оригинала 25 июль 2018 года. 2018 йыл 25 июль архивланған.
  25. [25]
    Round 2… 10 Trillion Digits of Pi
  26. [26]
    Pi - 12.1 Trillion Digits  (билдәһеҙ). www.numberworld.org. Дата обращения: 29 октябрь 2019.
  27. [27]
    Хоакин Наварро, 2014, с. 11.
  28. [28]
    Weisstein, Eric W. Мера иррациональности (инг.) на сайте Wolfram MathWorld.
  29. [29]
    Max A. Alekseyev On convergence of the Flint Hills series, 2011.
  30. [30]
    Weisstein, Eric W. Pi (инг.) на сайте Wolfram MathWorld.
  31. [31]
    Some unsolved problems in number theory
  32. [32]
    Weisstein, Eric W. Трансцендентное число (инг.) на сайте Wolfram MathWorld.
  33. [33]
    An introduction to irrationality and transcendence methods 2013 йыл 17 май архивланған.
  34. [34]
    Вездесущее число «пи», 2007, с. 67—69
  35. [35]
    Обман или заблуждение? 2012 йыл 30 ғинуар архивланған. Квант № 5 1983 год
  36. [36]
    Г. А. Гальперин. Биллиардная динамическая система для числа пи 2014 йыл 13 июнь архивланған..
  37. [37]
    «Элементарная геометрия» Киселёвастр. 225
  38. [38]
    21-Year-Old Memorises 70,000 Pi Digits, Sets Guinness Record
  39. [39]
    Chinese student breaks Guiness record by reciting 67,890 digits of pi
  40. [40]
    Interview with Mr. Chao Lu
  41. [41]
    How can anyone remember 100,000 numbers? — The Japan Times, 17.12.2006.
  42. [42]
    Pi World Ranking List
  43. [43]
  44. [44]
    The Indiana Pi Bill, 1897 (инг.)
  45. [45]
    В. И. Арнольд любит приводить этот факт, см. например книгу Что такое математика (ps), стр. 9.
  46. [46]
    Значение числа «пи» вычислили до 31,4 трлн знаков после запятой  (урыҫ). www.mk.ru. Дата обращения: 14 март 2019.
  47. [47]
    Статья в Los Angeles Times «Желаете кусочек π {\displaystyle \pi } {\displaystyle \pi }»? (название обыгрывает сходство в написании числа π {\displaystyle \pi } {\displaystyle \pi } и слова pie (англ. пирог)) 2009 йыл 19 февраль архивланған. (недоступная ссылка с 22-05-2013 (4165  дня) — история, копия) (инг.).
  • Жуков А. В. О числе π. — М.: МЦМНО, 2002. — 32 с. — ISBN 5-94057-030-5.
  • Жуков А. В. Вездесущее число «пи». — 2-е изд. — М.: Издательство ЛКИ, 2007. — 216 с. — ISBN 978-5-382-00174-6.
  • Кымпан, Флорика. История числа пи. — М.: Наука, 1971. — 217 с.
  • Наварро, Хоакин. Секреты числа π . {\displaystyle \pi .} {\displaystyle \pi .} Почему неразрешима задача о квадратуре круга. — М.: Де Агостини, 2014. — 143 с. — (Мир математики: в 45 томах, том 7). — ISBN 978-5-9774-0629-1.
  • Перельман Я. И. Квадратура круга. — Л.: Дом занимательной науки, 1941.. Переиздание: ЁЁ Медиа, ISBN 978-5-458-62773-3.
  • Шумихин Сергей, Шумихина Александра. Число Пи. История длиною в 4000 лет. — М.: Эксмо, 2011. — 192 с. — (Тайны мироздания). — ISBN 978-5-699-51331-4.
  • David H. Bailey, Jonathan M. Borwein. Pi: The Next Generation A Sourcebook on the Recent History of Pi and Its Computation. — Springer, 2016. — 507 с. — ISBN 978-3-319-32375-6.
  • Weisstein, Eric W. Pi Formulas (инг.) на сайте Wolfram MathWorld.
  • Различные представления числа Пи на Wolfram Alpha
  • эҙмә-эҙлелек A000796 OEIS
  • 22,4 трлн знаков числа пи (мировой рекорд)

Ҡалып:Числа с собственными именами Ҡалып:Иррациональные числа

Edit in WikipediaRevision historyRead in Wikipedia

Wikiwand in your browser!

Seamless Wikipedia browsing. On steroids.

Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.

Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.

Chrome
Wikiwand for Chrome
Edge
Wikiwand for Edge
Firefox
Wikiwand for Firefox

Үҙсәнлектәре

Тарихы

Рациональ яҡынлашыуҙары

Хәл ителмәгән проблемалар

Бюффон энәһе ысулы

Мнемоник ҡағиҙәләр

Өҫтәлмә факттар

Мәҙәниәттә

Шулай уҡ ҡарағыҙ

Иҫкәрмәләр

Әҙәбиәт

Һылтанмалар