五角反棱柱

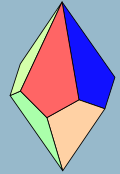
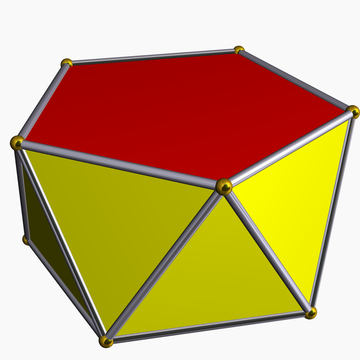
在幾何學中，五角反棱柱又稱為反五角柱或五角反柱是指底為五邊形的反棱柱，側面由三角形組成，若每一個面皆為正多邊形則稱為正五角反棱柱。每個五角反棱柱皆含有12個面，是一種十二面體。

正五角反棱柱

類別	反棱柱 柱狀均勻多面體
對偶多面體	五方偏方面體
識別
名稱	正五角反棱柱
參考索引	U77(c)
鮑爾斯縮寫 （verse-and-dimensions的wikia：Bowers acronym）	pap
數學表示法
考克斯特符號 （英语：Coxeter-Dynkin diagram）
施萊夫利符號	s{2,5}
威佐夫符號 （英语：Wythoff symbol）	| 2 2 5
康威表示法	A5
性質
面	12
邊	20
頂點	10
歐拉特徵數	F=12, E=20, V=10 （χ=2）
組成與佈局
面的種類	三角形×10 正五邊形×2
面的佈局 （英语：Face configuration）	10{3}+2{5}
頂點圖	3.3.3.5
對稱性
對稱群	D5d, [2+,10], (2*5), order 20
旋轉對稱群 （英語：Rotation_groups）	D5, [5,2]+, (522), order 10
特性
凸
圖像
3.3.3.5 （頂點圖） 五方偏方面體 （對偶多面體） （展開圖）

正五角反棱柱是基底為正五邊形的五角反棱柱，其可視為一種半正多面體。

正五角反棱柱也可以視為移除正二十面體底部及頂部的五角錐所構成的立體，因此又稱為正二十面體欠對二側錐。

• 
  正五角反棱柱

正五角反棱柱

當底面為正五邊形時，會具備一些特別的性質

當基底邊長為a的時候：

• 頂點數目：10
• 邊數目：20
• 面數目：12
• 對偶多面體：五方偏方面體
• 高：${\displaystyle a{\sqrt {{\frac {1}{10}}(5+{\sqrt {5}})}}}$
• 表面積：${\displaystyle {\frac {1}{2}}a^{2}(5+{\sqrt {3}}+{\sqrt {25+10{\sqrt {5}}}})}$
• 體積：${\displaystyle {\frac {1}{6}}a^{3}(5+2{\sqrt {5}})}$

相關多面體與鑲嵌

半正五邊形二面體球面多面體

對稱群（英语：List of spherical symmetry groups）：[5,2], (*522)							[5,2]+, (622)
{5,2}	t{5,2}	r{5,2}	2t{5,2}=t{2,5}	2r{5,2}={2,5}	rr{5,2}	tr{5,2}	sr{5,2}
半正對偶
V52	V102	V52	V4.4.5	V25	V4.4.5	V4.4.10	V3.3.3.5

半正反棱柱系列

2	3	4	5	6	7	8	9	10	11	12	n
s{2,4} sr{2,2}	s{2,6} sr{2,3}	s{2,8} sr{2,4}	s{2,10} sr{2,5}	s{2,12} sr{2,6}	s{2,14} sr{2,7}	s{2,16} sr{2,8}	s{2,18} sr{2,9}	s{2,20} sr{2,10}	s{2,22} sr{2,11}	s{2,24} sr{2,12}	s{2,2n} sr{2,n}
作為球面鑲嵌

參見

• 反棱柱
• 偏方面體

外部連結

• [1]（页面存档备份，存于互联网档案馆）