三角形

  「三角」跳轉到呢度。想搵其他用法，請睇「三角 (搞清楚)」。

  想搵第二個意思嘅話，請睇三角形 (搞清楚)。

  提示：呢篇文講嘅唔係ㅿ或Δ。

三角形係由三條線段順次首尾相連，組成嘅一個閉合嘅平面圖形，係最基本嘅多邊形。

一般用大寫英文字母${\displaystyle A}$、${\displaystyle B}$同${\displaystyle C}$為頂點標號。用小寫英語字母${\displaystyle a}$、${\displaystyle b}$同${\displaystyle c}$表示邊；${\displaystyle \alpha }$、${\displaystyle \beta }$同${\displaystyle \gamma }$或者頂點標號表示角。

基本概念

• 中線：三角形一邊中點同呢邊所對定點嘅連線段。
• 高線：由三角形一個頂點向佢嘅對邊所作嘅垂線段。
• 角平分線：平分三角形一角、一個端點喺呢一角嘅對邊上嘅線段。
• 中垂線：通過三角形一邊中點同該邊所垂直嘅線段，又叫做垂直平分線。

性質

定理

• 三角不等式：
  • 三角形兩邊嘅和大過第三邊，兩邊之差嘅絕對值小過第三邊。如果兩者相等，就係退化三角形。
  • 三角形任意一個外角大過唔相鄰嘅一個內角。

• 畢氏定理（又叫做畢達哥拉斯定理）同埋勾股逆定理：
  • 當直角三角形ABC嘅三頂點A、B、C所對嘅三邊分別為a、b、c，${\displaystyle a^{2}+b^{2}=c^{2}}$（當角C=90°）。

• 正弦定理（R係三角形外接圓半徑）：
  • ${\displaystyle {\frac {a}{\sin(\alpha )}}={\frac {b}{\sin(\beta )}}={\frac {c}{\sin(\gamma )}}=2R}$

• 餘弦定理：
  • ${\displaystyle a^{2}=b^{2}+c^{2}-2bc\cdot \cos(\alpha )}$
  • ${\displaystyle b^{2}=a^{2}+c^{2}-2ac\cdot \cos(\beta )}$
  • ${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cdot \cos(\gamma )}$

角度

三角形兩隻內角嘅和，等於剩落嚟嘅一隻外角。

喺歐幾里德平面內，三角形嘅內角和等於180°。

分類

銳角、鈍角三角形

鈍角三角形其中一隻角係鈍角（＞90°）嘅三角形，其餘兩角都＜90°。

銳角三角形嘅所有內角都係銳角（＜90°）。

直角三角形

有一個角係直角（＝90°）嘅三角形為直角三角形。

成直角嘅兩條邊稱為直角邊（cathetus），直角所對嘅邊係斜邊（hypotenuse）；或最長嘅邊稱為弦，底部嘅一邊稱作勾（又作句），另一邊稱為股。

可以透過唁同角度嘅直角三角形各邊嘅比求得銳角三角函數。

等邊三角形

等邊三角形（又叫正三角形），係三邊相等嘅三角形。三個內角相等，都係60°。佢係銳角三角形嘅一種。當佢嘅邊長係a，面積公式就係${\displaystyle {\frac {\sqrt {3}}{4}}a^{2}}$。

等邊三角形係正四面體、正八面體同正二十面體呢三個正多面體面嘅形狀。六個等邊三角形可以拼成一個正六邊形。

等腰三角形

等腰三角形係三條邊中有兩條邊相等（或者其中兩隻內角相等）嘅三角形。等腰三角形中嘅兩條相等嘅邊被稱為腰，而另一條邊被稱為底邊，兩條腰交叉組成嘅嗰個點被稱為頂點，佢哋組成嘅角被稱為頂角。

等腰三角形嘅重心、中心同垂心都位於頂點向底邊嘅垂線上。

等腰三角形嘅底嘅垂直平分線，啱啱亦係對應角嘅角平分線。

等邊三角形係等腰三角形嘅一個特殊形式。

退化三角形

退化三角形係指面積係零嘅三角形。滿足下列條件之一嘅三角形就可以稱為退化三角形：三個內角嘅度數為（180°,0°,0°）或（90°,90°,0°）；三邊其中一條邊嘅長度為0；一條邊嘅長度等於另外兩條嘅和。有人認為退化三角形唔算係三角形，咁係由於佢介乎於三角不等式之間，喺一啲資料中已否定咗其中一條邊等於其餘兩條邊嘅和嘅情況。

特性

三角形具有穩定性，若果兩個三角形有以下嘅邊角關係，佢嘅形狀、大細就唔會變，兩個三角形就係全等三角形。

• SSS（Side-Side-Side、邊、邊、邊）：各三角形嘅三條邊嘅長度都對應地相等。
• SAS（Side-Angle-Side、邊、角、邊）：各三角形嘅其中兩條邊嘅長度對應地相等，而且兩條邊夾住嘅角對應地相等。
• ASA（Angle-Side-Angle、角、邊、角）：各三角形嘅其中兩個角對應地相等，而且兩條邊夾住嘅邊對應地相等。
• RHS：喺直角三角形中，斜邊同埋另外一條直角邊對應地相等。
• AAS（Angle-Angle-Side、角、角、邊）：各三角形嘅其中兩個角對應地相等，而且其中一組對應角嘅對邊亦對應地相等。

AAA（Angle-Angle-Angle、角、角、角）只可以保證兩個三角形相似，唔可以保證全等。SSA（Side-Side-Angle、邊、邊、角）亦唔可以保證兩個三角形全等。

面積

已知兩邊同埋其夾角

當a、b係所知嘅兩邊，C係個夾角，三角形面積係${\displaystyle S={\frac {1}{2}}ab\sin {C}}$。

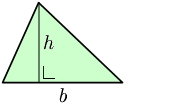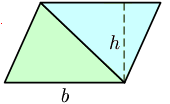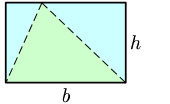
已知底同高

${\displaystyle S={\frac {1}{2}}bh}$，即底×高÷2。因為兩個相同嘅三角形砌到一個平行四邊形。

已知三邊長

希羅公式（又稱海倫公式、海龍公式）： 當p等於三角形三邊和嘅一半：

${\displaystyle p={\frac {a+b+c}{2}}}$

則

${\displaystyle S={\sqrt {p\left(p-a\right)\left(p-b\right)\left(p-c\right)}}}$

代入後就係：

${\displaystyle S={\frac {1}{4}}{\sqrt {\left(a+b+c\right)\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)}}}$

秦九韶亦求過類似嘅公式，稱為三斜求積法：

${\displaystyle {\sqrt {{\frac {1}{4}}\left(c^{2}a^{2}-\left({\frac {c^{2}+a^{2}-b^{2}}{2}}\right)^{2}\right)}}}$

基於希羅公式喺三角形擁有非常細嘅角度嗰時並唔係數值穩定，有一個變化嘅計法。當a ≥ b ≥ c，三角形面積為${\displaystyle {\frac {1}{4}}{\sqrt {(a+(b+c))(c-(a-b))(c+(a-b))(a+(b-c))}}}$

喺坐標系中已知三頂點座標

由${\displaystyle (x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})}$三個頂點構成嘅三角形，面積就係：

${\displaystyle {\frac {1}{2}}{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}}$

任三角形外心同內心半徑算面積法

若果已知三角形面積為x，三邊邊長分別為a、b、c，s係三角形周長（a+b+c）內心半徑（r）：

${\displaystyle x={\frac {1}{2}}sr}$

外心半徑（R）：

${\displaystyle x={\frac {abc}{4R}}}$

半形定理

喺三角形${\displaystyle ABC\,}$中， 三個角嘅正切同三邊有以下關係：

${\displaystyle \tan {\frac {A}{2}}={\frac {1}{b+c-a}}{\sqrt {\frac {\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}{a+b+c}}}}$

${\displaystyle \tan {\frac {B}{2}}={\frac {1}{a+c-b}}{\sqrt {\frac {\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}{a+b+c}}}}$

${\displaystyle \tan {\frac {C}{2}}={\frac {1}{a+b-c}}{\sqrt {\frac {\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}{a+b+c}}}}$

證明：

${\displaystyle \tan {\frac {A}{2}}={\frac {\sin {\frac {A}{2}}}{\cos {\frac {A}{2}}}}}$

因為：${\displaystyle \sin {\frac {A}{2}}>0}$

${\displaystyle \cos {\frac {A}{2}}>0}$

所以：${\displaystyle \sin {\frac {A}{2}}={\sqrt {\frac {1-\cos {A}}{2}}}={\sqrt {{\frac {1}{2}}\left(1-{\frac {b^{2}+c^{2}-a^{2}}{2bc}}\right)}}}$

${\displaystyle ={\sqrt {\frac {a^{2}+{\left(b-c\right)}^{2}}{4ac}}}}$

${\displaystyle ={\sqrt {\frac {\left(a+b-c\right)\left(a+c-b\right)}{4ac}}}}$

而：${\displaystyle \cos {\frac {A}{2}}={\sqrt {\frac {1+\cos {A}}{2}}}={\sqrt {{\frac {1}{2}}\left(1+{\frac {b^{2}+c^{2}-a^{2}}{2bc}}\right)}}}$

${\displaystyle ={\sqrt {\frac {{\left(b-c\right)}^{2}-a^{2}}{4ac}}}}$

${\displaystyle ={\sqrt {\frac {\left(b+c+a\right)\left(b+c-a\right)}{4ac}}}}$

所以：${\displaystyle \tan {\frac {A}{2}}={\frac {\sin {\frac {A}{2}}}{\cos {\frac {A}{2}}}}={\frac {\sqrt {\frac {\left(a+b-c\right)\left(a+c-b\right)}{4ac}}}{\sqrt {\frac {\left(b+c+a\right)\left(b+c-a\right)}{4ac}}}}={\sqrt {\frac {\left(a+b-c\right)\left(a+c-b\right)}{\left(b+c+a\right)\left(b+c-a\right)}}}}$

即：${\displaystyle \tan {\frac {A}{2}}={\frac {1}{b+c-a}}{\sqrt {\frac {\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}{a+b+c}}}}$

同理可得

${\displaystyle \tan {\frac {B}{2}}={\frac {1}{a+c-b}}{\sqrt {\frac {\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}{a+b+c}}}}$

${\displaystyle \tan {\frac {C}{2}}={\frac {1}{a+b-c}}{\sqrt {\frac {\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}{a+b+c}}}}$

用三角形嘅三邊表示角平分線長度

當喺三角形${\displaystyle ABC\,}$中，已知三邊${\displaystyle a\,}$，${\displaystyle b\,}$，${\displaystyle c\,}$，若果三個角${\displaystyle A\,}$,

${\displaystyle B\,}$，${\displaystyle C\,}$嘅角平分線分別係${\displaystyle t_{a}\,}$，${\displaystyle t_{b}\,}$，

${\displaystyle t_{c}\,}$，就用三邊表示三條內角平分線長度公式為

${\displaystyle t_{a}={\frac {1}{b+c}}{\sqrt {\left(a+b+c\right)\left(b+c-a\right)bc}}}$

${\displaystyle t_{b}={\frac {1}{a+c}}{\sqrt {\left(a+b+c\right)\left(a+c-b\right)ac}}}$

${\displaystyle t_{c}={\frac {1}{a+b}}{\sqrt {\left(a+b+c\right)\left(a+b-c\right)ab}}}$

其他三角形有關嘅定理

• 拿破崙三角形
• 費馬點
• 歐拉線
• 梅涅勞斯定理

三角形嘅五心

名稱	定義	備註
內心	三個內角嘅角平分線嘅交點	三角形內切圓嘅圓心
外心	三條邊嘅垂直平分線嘅交點	三角形外接圓嘅圓心
垂心	三條高嘅交點
形心（重心）	三條中線嘅交點	被交點劃分嘅線段比例為1:2（靠近角嘅一段較長）
旁心	外角嘅角平分線嘅交點	有三個，為三角形某一邊上嘅旁切圓嘅圓心

垂心（藍）、形心（黃）同外心（綠）能連成一線，稱為歐拉線。

外接圓同內切圓半徑

${\displaystyle R={\frac {abc}{\sqrt {\left(a+b+c\right)\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}}}}$

${\displaystyle r={\frac {\sqrt {\left(a+b+c\right)\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}}{2\left(a+b+c\right)}}}$

睇埋

• 三角學
• 多邊形