衛星測高

衛星測高（英語：Satellite Altimetry）是以人造衛星作為載體，使用雷達、雷射等測距技術量測衛星至地球表面的高度，從而獲取地球表面地形的空間測量技術。^[1][2]:187美國大地測量學家威廉·M·考拉（英語：William M. Kaula）於1969年召開的威廉斯敦固體地球和海洋物理大會上首次提出了衛星測高的概念，並將其視為研究固態地球與海洋動力學（英語：Ocean dynamics）的關鍵技術。^[3]

由TOPEX/Poseidon測高數據反演得到的海面高度，揭示了聖嬰現象帶來的海面異常起伏（圖中紅白色與藍紫色部分）

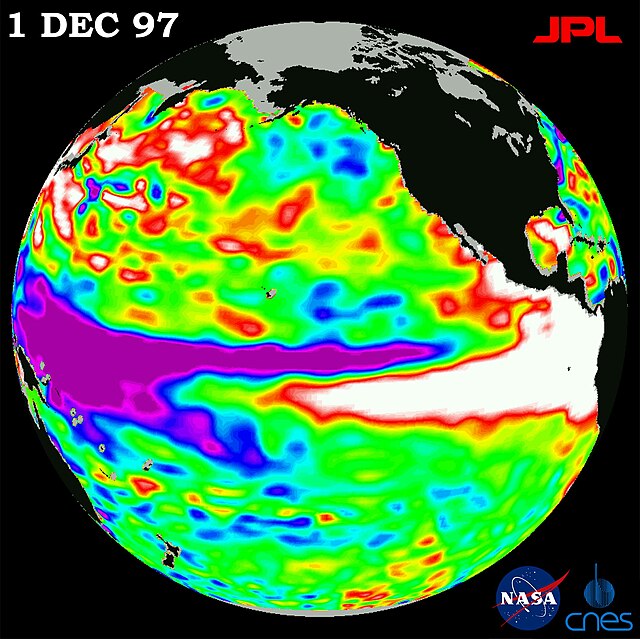
衛星測高能全天候、重複地提供全球範圍內的高度觀測值，被應用在海洋學、大地測量學、地球物理學及冰川學等各類地球科學的分支學科中，具體包括確定大地水準面與地球重力場、探測海山和深海海溝等海底地形、監測海面地形以反映大洋環流、潮汐和海平面上升等物理機制對海面高度的影響等等。^[4]以Geosat、ERS、TOPEX/Poseidon、Jason、ENVISAT、ICESat（英語：ICESat）等為代表的衛星測高任務，已參與入各類國際海洋和氣象計劃中。衛星測高技術也成為了全球氣候觀測系統（英語：Global Climate Observing System）（GCOS）和全球大地測量觀測系統（GGOS）的重要組成部分。^[2][5]

發展歷程

概念提出

由於水體具有良好的反射特性，雷達測高技術最初應用於海洋學的研究中。1969年，固體地球和海洋物理大會在美國麻薩諸塞州的威廉斯敦召開，大會上討論了雷達測高技術作為研究海洋學的空間技術的可行性。^[6]為達成這一目的，衛星測高技術需要同時具有精確測距與精確定軌的能力。^[7]

實驗階段

1973年至1974年間，NASA在其天空實驗室計劃（具體包括SL-2、SL-3及SL-4）中進行了人類歷史上的首次衛星測高實驗。在該實驗中，衛星高度約為750千米，測高精度約為1－2米，其中的誤差主要是來自於定軌精度的不足。隨著天空實驗室計劃的成功，衛星測高實驗很快得到了後續衛星任務的跟進：NASA在1975年至1979年間執行了GEOS-3（英語：GEOS-3）計劃，後又於1978年間執行了Seasat（英語：Seasat）計劃。這些後續任務配備的測高儀得到了改進，衛星本身的定軌精度也得到了提高。GEOS-3上除了搭載有雷達測高儀外，還搭載了雷射反射鏡、用於精確定軌的都卜勒發射器，以及衛星跟蹤衛星組件等。^[4]:144

成熟階段

1985年，由美國海軍運營的Geosat成功運作，標誌著衛星測高技術進入成熟階段，測距精度達到了10厘米以內。其後於1991年，歐空局也發射了其第一個地球觀測及測高衛星ERS-1。到1992年，由NASA和CNES聯合運營的TOPEX/Poseidon使用GPS與DORIS系統聯合定軌，將測距精度提高到了2－3厘米的級別，標誌著衛星測高技術進入了高精度時代。^[1]:3

基本原理

雷達高程測量

衛星測高原理示意圖

衛星測高技術通過有源測量的方式獲取衛星到地球表面的距離，這一過程通常是採用微波雷達實現。在衛星軌道上，星載雷達向天底方向發射高頻的脈衝信號，並接收地球表面反射的回波。^[8]之後，衛星通過比對分析得到信號的往返時間 ${\displaystyle \Delta t}$，再由光速 ${\displaystyle c}$ 求得衛星相對於地球表面的高度 ${\displaystyle \rho }$ ：^[4]:443

${\displaystyle \rho =c{\frac {\Delta t}{2}}}$

值得注意的是，衛星發射的雷達波束寬度約為1.5°－3°。根據衛星高度的不同，該波束在抵達地球表面時會產生一個半徑約為3－5千米的圓形區域。因此，測高儀測得的距離 ${\displaystyle \rho }$ 實際上是衛星到這個圓形區域的平均距離。^[2]:188-189

信號接收

在接收回波時，衛星會開啟一個長為數十米的窄帶分析窗口。信號進入窗口後，衛星將採用去斜脈衝壓縮的方式記錄下信號的波形和振幅。這些波形和振幅中包含有反射地物的特徵信息，以及因天線偏移產生的誤差。^[9]傳統的衛星任務採用「閉環模式（英語：closed-loop mode）」來記錄回波被接受到的時刻，而Jason-3（英語：Jason-3）及Sentinel-3（英語：Sentinel-3）等最新的衛星任務則使用所謂的「開環模式（英語：open-loop mode）」。在閉環模式中，衛星使用自適應跟蹤單元（英語：adaptive tracking unit，縮寫：ATU）分析回波；而在開環模式中，衛星會使用數字高程模型來獲得先驗的衛星高度，這主要是在陸地表面上使用。^[3]

基本觀測方程

通過衛星測高技術，可以獲得衛星星下點處，海水面及其他地球表面的大地高（橢球高） ${\displaystyle h}$。這一過程的原理由衛星測高基本觀測方程給出：^[10]:192

${\displaystyle h=r_{s}-{\hat {\rho }}-r_{e}-C}$

其中各個量的含義如下：

• ${\displaystyle r_{s}}$是衛星的地心距離，通過衛星的空間位置求得
• ${\displaystyle {\hat {\rho }}}$ 是由測高儀測得，並經誤差改正後的的衛星相對於海水面的高度
• ${\displaystyle r_{e}}$ 是衛星星下點的地心距離，該星下點位於參考橢球面上

特別地， ${\displaystyle C}$ 是因橢球法線與地心向徑的不重合而產生的改正項，量級通常在0至5米之間，其計算公式為：^[10]:192

${\displaystyle C={r_{e} \over 8}\left(1-{r_{e} \over r_{s}}\right)e^{4}\sin ^{2}2B}$

其中 ${\displaystyle e}$ 為參考橢球的偏心率， ${\displaystyle B}$為星下點的大地緯度。

誤差改正公式

衛星發射的脈衝信號在其傳播和處理中會受到各類因素的影響，使測高儀測得的距離 ${\displaystyle \rho }$ 實際上並不等於衛星到反射面的距離。為了得到這一實際距離的估計值 ${\displaystyle {\hat {\rho }}}$，需要對其進行誤差改正：^[2]:193

${\displaystyle {\hat {\rho }}=\rho +\Delta \rho _{sg}+\Delta \rho _{i}+\Delta \rho _{a}+\Delta \rho _{ssb}+\Delta \rho _{t}+\varepsilon }$

其中各類改正項及誤差項的具體含義為：

• ${\displaystyle \Delta \rho _{sg}}$ 為衛星發射與接受天線與衛星質心的偏差的改正項
• ${\displaystyle \Delta \rho _{i}}$ 為儀器誤差的改正項
• ${\displaystyle \Delta \rho _{a}}$ 為大氣傳播延遲的改正項，具體包括電離層延遲與對流層延遲，對流層延遲又可分為干延遲與濕延遲等
• ${\displaystyle \Delta \rho _{ssb}}$ 為電磁偏差改正項，由海面的波浪和地形起伏等因素造成
• ${\displaystyle \Delta \rho _{t}}$ 為潮汐改正，包括固體潮和海洋潮汐的改正等
• ${\displaystyle \varepsilon }$ 為殘餘的未改正誤差項

根據選取的改正項的不同，誤差改正公式的形式會存在差別。具體的影響因素參見誤差分析的章節。

誤差分析

測高衛星的主要誤差來源包括衛星軌道誤差、環境誤差與儀器誤差等。^[11][2]:190總體來看，以GEOS-3（英語：GEOS-3）、Seasat（英語：Seasat）、Geosat、ERS-1及TOPEX/Poseidon為例，各項誤差對其總誤差的貢獻為：^[2]:194

誤差類型		GEOS-3	Seasat	Geosat	ERS-1	TOPEX/Poseidon
軌道誤差	重力場	50 cm	25 cm	15 cm	15 cm	小於2 cm
	輻射壓		15 cm	10 cm	6 cm	小於2 cm
	大氣阻力		15 cm	10 cm	6 cm	小於2 cm
	重力常數				2 cm	1 cm
	潮汐		12 cm	5 cm	5 cm	小於2 cm
	對流層		5 cm	4 cm	2 cm	1 cm
	測站位置		10 cm	5 cm	3 cm	1 cm
	總誤差	50 cm	30 cm	20 cm	18 cm	3.5 cm
儀器誤差	儀器噪聲	50 cm	10 cm	5 cm	3 cm	小於2 cm
	儀器偏差		7 cm	5 cm	3－5 cm	2 cm
	鍾偏差		5 ms	3－5 ms	1－2 ms	小於2 ms
	總誤差	50 cm	15 cm	7 cm	5 cm	2 cm
環境誤差	電磁偏差	10 cm	5 cm	2 cm	2 cm	小於2 cm
	波形偏差	2 cm	1 cm	1 cm	1 cm	1 cm
	干延遲	2 cm	2 cm	1 cm	1 cm	1 cm
	濕延遲	2 cm	2 cm	1 cm	1 cm	1 cm
	電離層延遲	2－3 cm	2－3 cm	2－3 cm	2－3 cm	1.3 cm
	總誤差	20 cm	10 cm	6 cm	4 cm	3.5 cm

軌道誤差

軌道誤差因衛星真實運行的軌道與計算軌道的偏差引起，且影響具有長波性質^[2]:190，主要包括如下幾項：

• 地球重力場解析度和精度的不足
• 地面跟蹤站的位置誤差
• 衛星跟蹤系統（如DORIS系統）的誤差
• 用於計算軌道的模型中存在的偏差

模型誤差

地球重力場在早期的衛星測高任務中是軌道誤差中起主導作用的誤差項。每顆衛星都對重力場中某一組特定的球諧係數非常敏感。因此，較為可行的方案是利用對衛星自身的觀測數據，或是對相近衛星的觀測數據，來製作一個為其專門定製的重力場模型。但隨著EGM96、JGM-3等高階次重力場模型的出現，重力場模型在徑向上的精度可以達到10厘米內，已不再在軌道誤差中起主導作用。^[4]:454-455

潮汐誤差

日、月等天體會影響地球的整體形態，從而造成地球重力場的變化。這主要包括海洋潮汐、固體潮汐、極潮汐和負荷潮汐等，其引起的變化從數厘米到數米不等，在某些近海附近甚至可以達到數十米。^[12]這些變化可以通過潮汐模型進行改正，當前潮汐模型的精度則在數厘米左右。^[2]:191

環境誤差

環境誤差包括大氣傳播延遲和由地球表面在對電磁波的反射、散射等的過程中引起的誤差。

電離層延遲

電離層延遲是由脈衝信號在穿過大氣電離層時，與大氣中的帶電粒子等產生各類物理效應而產生的時間延遲差，最主要的影響來自於電離層的折射效應。該延遲的量級與太陽及其他天體的輻射強度、季節、時間和地理位置等因素的影響，延遲量在0.2－20厘米不等，在夜間及太陽活動不頻繁的時期較小。若衛星攜帶有雙頻測高儀（例如TOPEX/Poseidon，使用的是6GHz的C波段和13.5GHz的Ku波段），則可對電離層延遲進行直接改正。除此之外，電離層延遲也可通過模型或DORIS測量改正。^[13][14]

對流層延遲

對流層延遲分為濕延遲部分和干延遲部分。其中濕延遲部分由雲層中的液態水及大氣中的水蒸氣引起，量級在0－50厘米之間，受氣象條件的影響變化較大；干延遲部分則是由乾燥氣體引起，量級約為2.3米，並且較為穩定。^[12]

電磁偏差

電磁偏差是因海面波谷反射脈衝的能力較波峰更強，使得回波功率的重心趨向波谷而非海面中心帶來的偏移，也即平均散射面與平均海面的偏移。利用機載雷達和雷射系統對海面反射特性的研究發現，該偏移是由海波引起的海面地形的偏度、峰度，以及海面風速的函數，量級在0到50厘米之間。^[15]以TOPEX/Poseidon採用的四參數改正模型為例，其形式為：^[16]

${\displaystyle \rho _{ssb}={\text{SWH}}\left[a_{1}+a_{2}{\text{SWH}}+a_{3}U+a_{5}U^{2}\right]}$

其中，${\displaystyle {\text{SWH}}}$ 是有效波高，${\displaystyle U}$ 是估算風速，${\displaystyle a_{1}}$、${\displaystyle a_{2}}$、${\displaystyle a_{3}}$ 和 ${\displaystyle a_{5}}$ 是常係數。

儀器誤差

儀器誤差主要包括下列因素：^[17][4]:457

• 因天線的相位中心與太空飛行器的質心產生的偏移
• 信號在測高儀內部的電子器件中的傳播延遲
• 測量系統採用的時間系統中存在的誤差

測高衛星

截至2020年，已經結束或正在運行的測高衛星任務有如下幾項：^[18]

任務	圖像	運營方	開始時間	結束時間	高度	傾角	使用頻段	重複周期	測高儀	測距精度
天空實驗室 Skylab		NASA	1973年	1974年	435 km	50°			S193	1 m
GEOS-3（英語：GEOS-3）		NASA	1975年	1979年	845 km	115°			ALT	25 cm
Seasat（英語：Seasat）		NASA	1978年	1978年	800 km	108°	Ku波段	約17天	ALT	5 cm
Geosat		美國海軍	1985年	1990年	800 km	108°	Ku波段	4天/17天		4 cm
歐洲遙感衛星 ERS-1		ESA	1991年	2000年	785 km	98.5°	Ku波段	3天/35天/168天	RA	3 cm
TOPEX/Poseidon		NASA	1992年	2006年	1336 km	98.5°	Ku波段、C波段	3天/35天/168天	TOPEX	2 cm
		CNES					Ku波段		Poseidon-1
歐洲遙感衛星 ERS-2		ESA	1995年	2011年	785 km	98.5°	Ku波段	35天	RA	3 cm
GFO		美國海軍 NOAA	1998年	2008年	800 km	108°	Ku波段	17天	GFO-RA	3.5 cm
Jason-1		CNES NASA	2001年	2013年	1336 km	66°	Ku波段、C波段	10天	Poseidon-2	2 cm
歐洲環境衛星 Envisat		ESA	2002年	2012年	800 km	98.5°	Ku波段、S波段	35天	RA-2	2－3 cm
OSTM/Jason-2（英語：OSTM/Jason-2）		CNES NASA EUMETSAT（英語：European Organisation for the Exploitation of Meteorological Satellites） NOAA	2008年	2019年	1336 km	66°	Ku波段、C波段	10天	Poseidon-3
CryoSat-2（英語：CryoSat-2）		ESA	2010年	正在運行	720 km	92°	Ku波段、C波段	369天	SIRAL
海洋二號A HY-2A		中國	2011年	正在運行	963 km	99.3°	Ku波段、C波段	14天/168天
SARAL（英語：SARAL）		ISRO CNES	2013年	正在運行	800 km	92°	Ka波段	35天	AltiKa
Sentinel-3（英語：Sentinel-3）		ESA	2016年	正在運行	814 km	98.5°	Ku波段、C波段	27天	SRAL
Jason-3（英語：Jason-3）		CNES NASA EUMETSAT（英語：European Organisation for the Exploitation of Meteorological Satellites） NOAA	2016年	正在運行	1336 km	66°	Ku波段、C波段	10天	Poseidon-3

學科應用

大地測量學

在海洋部分，衛星測高量取的是海水面的形狀。而根據大地水準面的經典定義，其是與平均海水面最為密合的重力等位面。因而，衛星測高數據在去除時變因素與穩態的海面地形後，亦能用於建立高解析度的大地水準面。除此之外，衛星測高數據還可進一步用於確定重力異常、垂線偏差等地球重力場中重要的物理量。儘管當前如何區分平均海面地形和大地水準面尚未完全解決，而且還是海洋大地測量學中最具挑戰性的問題之一，但衛星測高所提供的空前豐富的數據，仍是確定地球重力場最為經濟且有效的手段。^[2][4]

數學原理

極軌衛星ENVISAT的地面軌跡，其中自南向北運動的弧段為升弧段，自北向南運動的弧段為降弧段

主條目：垂線偏差

地球重力場中的其他物理量可以通過地球表面的垂線偏差計算而得，因此在此僅以垂線偏差的計算原理為例。衛星的地面軌跡在地表上存在有交叉點，按其經過交叉點時的方向，可將交叉的兩條軌跡分為升弧和降弧。交叉點處的垂線偏差則利用測高數據量取的大地水準面高 ${\displaystyle N}$ 及其偏導數計算得出。這一垂線偏差由其在子午圈上的分量 ${\displaystyle \xi }$ 及其在卯酉圈上的分量 ${\displaystyle \eta }$ 表示：^[19]

${\displaystyle {\begin{cases}\xi =-{\frac {1}{R}}{\partial N \over \partial \varphi }\\\eta =-{\frac {1}{R\cos \varphi }}{\partial N \over \partial \lambda }\end{cases}}}$

式中，${\displaystyle R}$ 為地球的平均半徑，${\displaystyle (\varphi ,\lambda )}$則為該交叉點的大地緯度和大地經度。其中大地水準面高在經度和緯度上的偏導數的計算公式則由大衛·T·桑德威爾（英語：David T. Sandwell）提出：^[20]

${\displaystyle {\begin{cases}{\partial N \over \partial \lambda }={\frac {1}{2{\dot {\lambda }}}}({\dot {N}}_{a}+{\dot {N}}_{d})\\{\partial N \over \partial \varphi }={\frac {1}{2{\dot {\varphi }}}}({\dot {N}}_{a}-{\dot {N}}_{d})\end{cases}}}$

其中，${\displaystyle ({\dot {\varphi }},{\dot {\lambda }})}$是衛星在經過該交叉點時的速度分量，${\displaystyle {\dot {N}}_{a}}$和${\displaystyle {\dot {N}}_{d}}$則分別是大地水準面高在升弧和降弧段對時間的偏導數，這四個量都可以通過衛星測高觀測數據計算得到。

地球物理學

通過Geosat、ERS及TOPEX/Poseidon的測高數據，可以構建出海洋的重力場模型。重力場模型中的重力異常和大地水準面擾動的分布，則反映了海山、洋脊和海溝等海底地形，以及莫霍面深度、地函對流等更深層的地球內部結構的影響。具體地，大尺度的地函對流影響的是重力場中的長波部分，而岩石圈等較淺的密度異常影響的則是重力場中的短波部分。^[2][4][21]

海洋學

由TOPEX/Poseidon提供的數據繪製的全球海面地形分布圖

1880年－2015年的海平面高度變化，衛星測高數據（藍線）可用於提供有關海面變化的數據

在物理海洋學中，測高數據被用於研究海平面的空間變化與時間變化。通過測高數據，可以得到海水面的分布特徵，其相對於地球重力場中與其最為密合的等位面（即大地水準面）的起伏被稱為海面地形（英語：Sea Surface Topography，縮寫：SST）。這一起伏又被分為兩類，一類是由於大洋環流、潮汐和大氣作用所引起的瞬時海水面的起伏，另一類是剔除了部分或全部時變因素後得到的擬穩態或穩態海水面起伏。^[2]:216在已知大地水準面高 ${\displaystyle N}$ 的情況下，海水面的大地高 ${\displaystyle h}$ 可直接轉化為海面地形 ${\displaystyle H}$：^[4]:451

${\displaystyle H=h-N}$

由此得到的海面地形去除了地球重力的影響，包含了有關海流和潮汐等海洋學研究的關鍵信息。

大洋環流

大洋環流因與地球的自轉偏向力達成地轉平衡（英語：geostrophic balance）的水平壓力梯度而引起，其使海面地形出現的起伏可達到一米左右的程度。因此，洋流路線的季節性變化足以被測高衛星探測得到。^[22]以墨西哥灣暖流為例，在GEOS-3（英語：GEOS-3）分別於1977年4月和同年9月經過同一地點上空時，探測到的海水面高度發生了1.2米的變化，而附近區域因海山造成的海水面起伏則幾乎沒有改變。^[23]此外，洋流流量的變化也會引起海面地形的波動，其中季節性的影響因素可以達到大約0.1米，這種波動則可由TOPEX/Poseidon等高時間解析度的測高衛星發現。^[24][25][26]

海洋潮汐

海洋潮汐是造成平均海平面變化的最大影響因素，量級約為30厘米。重複的測高數據可以用於全球海面的潮汐監測，並參與到潮汐預測的數學模型中。以TOPEX/Poseidon為例，使用其提供的測高數據建立的潮汐模型可以達到2－3厘米的精度。^[27][28]

海面變化

海平面變化既包含有周期性的波動，也包含有人類活動帶來的影響，這一結果已被全球性的驗潮資料證實。對衛星在其軌跡上同一點獲得的重複觀測數據進行時間序列分析發現，海平面的周年變化幅度可以達20厘米，形成這類周年變化的原因則是不同季節的溫度變化。^[29]聖嬰等現象造成的海水溫度變化，也可以給海平面高度帶來10厘米左右的改變。因此，衛星測高的數據也可以用於研究全球的氣候變化，甚至提前數月就監測到海面測量無法發覺的聖嬰信號。^[30][31]TOPEX/Poseidon及其後的Jason系列任務的長期監測，已經發現了周期在10年以上的濤動現象。^[32][33]除此之外，這些測高數據還顯示出，人類活動造成的海平面上升速率則約為3－4毫米每年。^[34][35]

海況監測

平靜的海水面是良好的反射體，當海面受到風浪等因素的干擾時，其反射特性也會發生變化。這些特徵能反映在回波的波形和強度上：較為平靜的海面反射的脈衝信號較強，而起伏不定的海面反射的脈衝信號較弱。因此，通過分析雷達測高信號可以得到相關的海況數據，並進一步用於建立預測模型、為船上運輸等海上人類活動提供相關情報等。^[36][37]

相關條目

• 空間大地測量學
  • 衛星大地測量學（英語：Satellite geodesy）

• 大地水準面
• 高程系統
• 人造衛星
• 月球雷射測距實驗

參考文獻

1. Frappart, Frédéric; Blumstein, Denis; Cazenave, Anny; Ramillien, Guillaume; Birol, Florence; Morrow, Rosemary; Rémy, Frédérique. Satellite Altimetry: Principles and Applications in Earth Sciences. Wiley Encyclopedia of Electrical and Electronics Engineering. American Cancer Society. 2017: 1–25 [2020-04-24]. ISBN 978-0-471-34608-1. doi:10.1002/047134608x.w1125.pub2. （原始內容存檔於2020-05-03） （英語）.
2. 李征航; 魏二虎; 王正濤; 彭碧波. 空间大地测量学. 武漢大學出版社. : 187–223. ISBN 978-7-30-707574-0.
3. Stammer, Detlef; Cazenave, Anny. Satellite Altimetry Over Oceans and Land Surfaces. CRC Press. 2017-10-31 [2020-04-24]. ISBN 978-1-351-64781-6. （原始內容存檔於2020-05-03） （英語）.
4. Sansó, Fernando. Satellite Geodesy, 2nd Edition G. Seeber, de Gruyter, 2003, ISBN 3-11-017549-5, Softback, 589 pp, Euro 84.00, sFR 134.00, US$ 79.95. Geophysical Journal International. 2004-04-01, 157 (1): 443–468 [2020-04-24]. ISSN 0956-540X. doi:10.1111/j.1365-246X.2004.02236.x. （原始內容存檔於2020-05-03） （英語）.
5. THE GLOBAL GEODETIC OBSERVING SYSTEM (PDF). ilrs.gsfc.nasa.gov. 2007-10-15 [2020-04-25]. （原始內容存檔 (PDF)於2020-05-03） （英語）.
6. THE TERRESTRIAL ENVIRONMENT: SOLID-EARTH AND OCEAN PHYSICS (PDF). WASHINGTON, D.C.: NATIONAL AERONAUTICS AND SPACE ADMINISTRATION. 1970-04 [2020-04-24]. （原始內容 (PDF)存檔於2020-05-03）.
7. History: Aviso+. www.aviso.altimetry.fr. [2020-04-25]. （原始內容存檔於2020-05-14） （英語）.
8. Basic principle: Aviso+. www.aviso.altimetry.fr. [2020-04-25]. （原始內容存檔於2020-05-03）.
9. Fu, Lee-Lueng; Cazenave, Anny. Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications. Elsevier. 2000-11-09 [2020-04-25]. ISBN 978-0-08-051658-5. （原始內容存檔於2020-05-03） （英語）.
10. Rummel, Reiner. Principle of satellite altimetry and elimination of radial orbit errors. Rummel, Reiner (編). Satellite Altimetry in Geodesy and Oceanography. Lecture Notes in Earth Sciences. Berlin, Heidelberg: Springer. 1993: 190–241. ISBN 978-3-540-47758-7. doi:10.1007/bfb0117929 （英語）.
11. 5.2.2 Data processing – Radar Altimetry Tutorial and Toolbox. [2020-04-26]. （原始內容存檔於2020-12-04） （美國英語）.
12. 5.2.2.3 Geophysical corrections – Radar Altimetry Tutorial and Toolbox. [2020-04-26]. （原始內容存檔於2020-08-06） （美國英語）.
13. Imel, David A. Evaluation of the TOPEX/POSEIDON dual-frequency ionosphere correction. Journal of Geophysical Research: Oceans. 1994, 99 (C12): 24895–24906 [2020-04-26]. ISSN 2156-2202. doi:10.1029/94JC01869. （原始內容存檔於2020-06-08） （英語）.
14. 5.2.2.3.3 Ionosphere corrections – Radar Altimetry Tutorial and Toolbox. [2020-04-26]. （原始內容存檔於2020-11-09） （美國英語）.
15. 5.2.2.3.7. Electromagnetic bias – Radar Altimetry Tutorial and Toolbox. [2020-04-26]. （原始內容存檔於2020-11-13） （美國英語）.
16. Gaspar, Philippe; Ogor, Françoise; Le Traon, Pierre-Yves; Zanife, Ouan-Zan. Estimating the sea state bias of the TOPEX and POSEIDON altimeters from crossover differences. Journal of Geophysical Research. 1994, 99 (C12): 24981. ISSN 0148-0227. doi:10.1029/94JC01430 （英語）.
17. 5.2.2.4 Instrumental errors – Radar Altimetry Tutorial and Toolbox. [2020-04-26]. （原始內容存檔於2020-11-09） （美國英語）.
18. 7. Missions – Radar Altimetry Tutorial and Toolbox. [2020-04-24]. （原始內容存檔於2020-11-27） （美國英語）.
19. 寧津生. 管澤霖 , 編. 地球形状及外部重力场. 測繪出版社. 1981: 243–249.
20. Sandwell, David T. Geophysical Applications of Satellite Altimetry. RvGeo. 1991-05, 29 (S1): 132–137 [2020-04-27]. ISSN 8755-1209. doi:10.1002/(ISSN)1944-9208. （原始內容存檔於2020-05-03） （英語）.
21. Gao, Jinyao; Jin, Xianglong. Hwang, Cheinway , 編. Joint Application of Altimeter Data and EGM96 to Submarine Tectonic and Geodynamic Study in West Pacific. Satellite Altimetry for Geodesy, Geophysics and Oceanography. International Association of Geodesy Symposia (Berlin, Heidelberg: Springer). 2004: 133–142 [2020-04-28]. ISBN 978-3-642-18861-9. doi:10.1007/978-3-642-18861-9_16. （原始內容存檔於2020-05-03） （英語）.
22. Fu, Lee-lueng; Vazquez, Jorge; Parke, Michael E. Seasonal variability of the Gulf Stream from satellite altimetry. Journal of Geophysical Research: Oceans. 1987, 92 (C1): 749–754 [2020-04-26]. ISSN 2156-2202. doi:10.1029/JC092iC01p00749. （原始內容存檔於2020-05-03） （英語）.
23. Cheney, Robert E.; Douglas, Bruce C.; Sandwell, David T.; Marsh, James G.; Martin, Thomas V.; McCarthy, John J. Applications of satellite altimetry to oceanography and geophysics. Marine Geophysical Researches. 1984-03-01, 7 (1): 17–32. ISSN 1573-0581. doi:10.1007/BF00305408 （英語）.
24. Vivier, Frédéric; Provost, Christine. Volume transport of the Malvinas Current: Can the flow be monitored by TOPEX/POSEIDON?. Journal of Geophysical Research: Oceans. 1999, 104 (C9): 21105–21122 [2020-04-26]. ISSN 2156-2202. doi:10.1029/1999JC900056. （原始內容存檔於2020-05-03） （英語）.
25. Han, Guoqi; Tang, C. L. Interannual Variations of Volume Transport in the Western Labrador Sea Based on TOPEX/Poseidon and WOCE Data. Journal of Physical Oceanography. 2001-01-01, 31 (1): 199–211 [2020-04-26]. ISSN 0022-3670. doi:10.1175/1520-0485(2001)0312.0.CO;2. （原始內容存檔於2020-05-03）.
26. Hwang, Cheinway; Kao, Ricky. TOPEX/POSEIDON-derived space–time variations of the Kuroshio Current: applications of a gravimetric geoid and wavelet analysis. Geophysical Journal International. 2002-12-01, 151 (3): 835–847 [2020-04-26]. ISSN 0956-540X. doi:10.1046/j.1365-246X.2002.01811.x. （原始內容存檔於2020-05-03） （英語）.
27. Desai, Shailen D.; Wahr, John M. Empirical ocean tide models estimated from TOPEX/POSEIDON altimetry. Journal of Geophysical Research: Oceans. 1995, 100 (C12): 25205–25228 [2020-04-26]. ISSN 2156-2202. doi:10.1029/95JC02258. （原始內容存檔於2020-05-03） （英語）.
28. Fu, Lee-Lueng; Chelton, Dudley B. Chapter 2 Large-Scale Ocean Circulation. Fu, Lee-Lueng (編). International Geophysics. Satellite Altimetry and Earth Sciences 69. Academic Press. 2001-01-01: 133–viii [2020-04-26]. doi:10.1016/s0074-6142(01)80147-9. （原始內容存檔於2020-05-03） （英語）.
29. Cazenave, A.; Dominh, K.; Ponchaut, F.; Soudarin, L.; Cretaux, J. F.; Provost, C. Le. Sea level changes from Topex-Poseidon altimetry and tide gauges, and vertical crustal motions from DORIS. Geophysical Research Letters. 1999, 26 (14): 2077–2080 [2020-04-27]. ISSN 1944-8007. doi:10.1029/1999GL900472. （原始內容存檔於2020-05-03） （英語）.
30. Chambers, D. P.; Chen, J. L.; Tapley, B. D. Identification of El Niño Signals with Satellite Altimetry. ITN. 1999-05, 26: 5–12 [2020-04-27]. （原始內容存檔於2020-05-03） （英語）.
31. Latest El Niño/La Niña Watch Data. sealevel.jpl.nasa.gov. [2020-04-27]. （原始內容存檔於2020-08-11）.
32. Hamlington, Benjamin; Leben, Robert; Strassburg, Mathew; Nerem, Robert; Kim, K.-Y. Contribution of the Pacific Decadal Oscillation to global mean sea level trends. Geophysical Research Letters. 2013-10-16, 40: 5171–5175. doi:10.1002/grl.50950.
33. Ariana, Dewi; Kusmana, Cecep; Setiawan, Yudi. STUDY OF SEA LEVEL RISE USING SATELLITE ALTIMETRY DATA IN THE SEA OF DUMAI, RIAU, INDONESIA. Geoplanning: Journal of Geomatics and Planning. 2017-01-26, 4: 75. doi:10.14710/geoplanning.4.1.75-82.
34. TOPEX/Poseidon Mean Sea Level Rise Observations to be Revised. NASA/JPL. [2020-04-27]. （原始內容存檔於2020-05-03）.
35. Cazenave, Anny; Palanisamy, Hindumathi; Ablain, Michael. Contemporary sea level changes from satellite altimetry: What have we learned? What are the new challenges?. Advances in Space Research. 2018-10-01, 62 (7): 1639–1653 [2020-04-27]. ISSN 0273-1177. doi:10.1016/j.asr.2018.07.017. （原始內容存檔於2020-05-03） （英語）.
36. Ocean forecasting and altimetry. sealevel.jpl.nasa.gov. [2020-04-27]. （原始內容存檔於2020-05-03）.
37. Barratt, Mark. The use of radar altimeter products at ECMWF. ECMWF. 2016-11-08 [2020-04-27]. （原始內容存檔於2020-05-03） （英語）.

外部連結

• 衛星海洋學存檔數據中心Aviso+ （CNES） （頁面存檔備份，存於網際網路檔案館）（英語）
• 雷達測高教程與工具箱（ESA&CNES） （頁面存檔備份，存於網際網路檔案館）（英語）