中央極限定理 （英語：central limit theorem，簡作 CLT ）是機率論 中的一組定理。在機率論中，中央極限定理 (CLT) 確認，在許多情況下，對於獨立並同樣分布的隨機變數，即使原始變量本身不是常態分布 ，標準化樣本均值的抽樣分布也趨向於標準常態分布 . 這組定理是數理統計學 和誤差 分析的理論基礎，指出了大量隨機變數之和近似服從常態分布 的條件。
10,000 次拋擲硬幣實驗中出現正面的平均比率，每次抽樣（實驗）的樣本數為 200（拋擲 200 次硬幣）
Tijms (2004, p.169) 寫到：
“
中央極限定理有著有趣的歷史。這個定理的第一版被法國 數學家 棣美弗 發現，他在1733年發表的卓越論文中使用常態分布 去估計大量拋擲硬幣出現正面次數的分布。這個超越時代的成果險些被歷史遺忘，所幸著名法國數學家拉普拉斯 在1812年發表的巨著 Théorie Analytique des Probabilités 中拯救了這個默默無名的理論。
拉普拉斯 擴展了棣美弗 的理論，指出二項分布 可用常態分布逼近。但同棣美弗 一樣，拉普拉斯 的發現在當時並未引起很大反響。直到十九世紀末中央極限定理的重要性才被世人所知。1901年，俄國數學家里雅普諾夫 用更普通的隨機變數定義中央極限定理並在數學上進行了精確的證明。如今，中央極限定理被認為是（非正式地）機率論 中的首席定理。
”
用常態分布逼近二項分布 棣莫佛 -拉普拉斯 定理（De Moivre–Laplace theorem）是中央極限定理的最初版本，討論了服從二項分布 的隨機變數序列。它指出，參數為n, p的二項分布以np為均值、np(1-p) 為變異數的常態分布為極限。
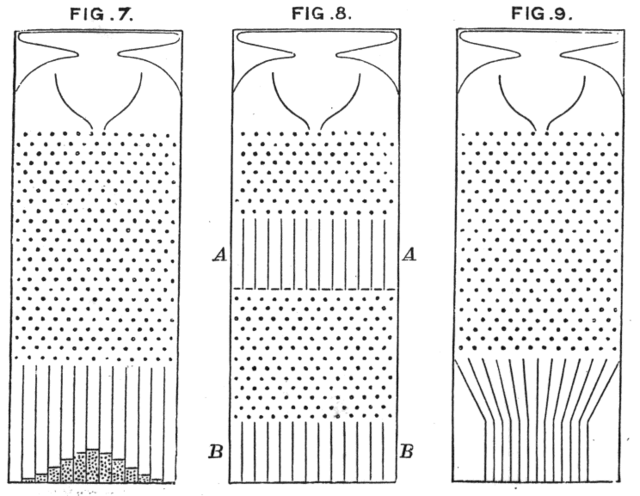
高爾頓繪製的高爾頓板模型，其中的小球顯出鐘形曲線。 棣美弗-拉普拉斯定理指出二項分布的極限為常態分布。高爾頓板可以看作是伯努利試驗的實驗模型。如果我們把小球碰到釘子看作一次實驗，而把從右邊落下算是成功，從左邊落下看作失敗，就有了一次
p
=
1
2
{\displaystyle p={\frac {1}{2}}}
中央極限定理的動態展示，獨立同分布隨機變數之和趨近常態分布。 林德伯格 萊維 （Lindeberg-Levy）定理，是棣莫佛-拉普拉斯定理的擴展，討論獨立同分布 隨機變數序列的中央極限定理。它表明，獨立同分布 （i.i.d., 即 independent and identically distributed）、且數學期望值和變異數有限的隨機變數序列的標準化和以標準常態分布為極限：
設隨機變數
X
1
,
X
2
,
⋯
,
X
n
{\displaystyle X_{1},X_{2},\cdots ,X_{n}}
數學期望值 和變異數
E
(
X
i
)
=
μ
{\displaystyle E(X_{i})=\mu }
D
(
X
i
)
=
σ
2
≠
0
(
i
=
1
,
2
,
⋯
,
n
)
{\displaystyle D(X_{i})=\sigma ^{2}\neq 0(i=1,2,\cdots ,n)}
X
¯
=
1
n
∑
i
=
1
n
X
i
{\displaystyle {\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}}
ζ
n
=
X
¯
−
μ
σ
/
n
{\displaystyle \zeta _{n}={\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}}
lim
n
→
∞
P
(
ζ
n
≤
z
)
=
Φ
(
z
)
{\displaystyle \lim _{n\rightarrow \infty }P\left(\zeta _{n}\leq z\right)=\Phi \left(z\right)}
其中
Φ
(
z
)
{\displaystyle \Phi (z)}
林德伯格 不同分布 的情況下的隨機變數和。它表明，滿足一定條件時，獨立的，但不同分布的隨機變數序列的標準化和依然以標準常態分布為極限：
記隨機變數序列
X
i
{\displaystyle X_{i}}
X
i
{\displaystyle X_{i}}
E
[
X
i
]
=
0
{\displaystyle E[X_{i}]=0}
S
n
=
∑
i
=
1
n
X
i
{\displaystyle S_{n}=\sum _{i=1}^{n}X_{i}}
記
s
i
2
=
V
a
r
(
X
i
)
{\displaystyle s_{i}^{2}={\rm {Var}}(X_{i})}
σ
n
2
=
∑
i
=
1
n
s
i
2
=
V
a
r
(
S
n
)
{\displaystyle \sigma _{n}^{2}=\sum _{i=1}^{n}s_{i}^{2}={\rm {Var}}(S_{n})}
如果對每個
ϵ
>
0
{\displaystyle \epsilon >0}
lim
n
→
∞
1
σ
n
2
∑
i
=
1
n
E
[
X
i
2
;
{
|
X
i
|
>
ϵ
σ
n
}
]
=
0
{\displaystyle \lim _{n\rightarrow \infty }{1 \over \sigma _{n}^{2}}\sum _{i=1}^{n}E[X_{i}^{2};\{|X_{i}|>\epsilon \sigma _{n}\}]=0}
則稱它滿足林德伯格（Lindeberg）條件。
滿足此條件的序列趨向於常態分布，即
S
n
/
σ
n
→
d
N
(
0
,
1
)
{\displaystyle S_{n}/\sigma _{n}{\stackrel {d}{\rightarrow }}N(0,1)}
同時，該條件也是期望值為零、變異數有限的獨立變量之和趨於常態分布的必要條件。
與之相關的是李亞普諾夫 （Lyapunov）條件：
E
[
|
X
i
|
3
]
<
∞
,
lim
n
→
∞
1
σ
n
3
∑
i
=
1
n
E
[
|
X
i
|
3
]
=
0
{\displaystyle E[|X_{i}|^{3}]<\infty ,\,\lim _{n\rightarrow \infty }{1 \over \sigma _{n}^{3}}\sum _{i=1}^{n}E[|X_{i}|^{3}]=0}
滿足李亞普諾夫條件的序列，必滿足林德伯格條件。
在此只對較強的李亞普諾夫條件給出證明。
以下證明對每一實數
t
{\displaystyle t}
φ
S
n
/
σ
n
(
t
)
→
e
−
t
2
/
2
{\displaystyle \varphi _{S_{n}/\sigma _{n}}(t)\rightarrow e^{-t^{2}/2}}
|
φ
S
n
/
σ
n
(
t
)
−
e
−
t
2
/
2
|
=
|
∏
k
=
1
n
φ
X
k
(
t
/
σ
n
)
−
∏
k
=
1
n
e
−
t
2
s
k
2
/
2
σ
n
2
|
≤
∑
k
=
1
n
|
φ
X
k
(
t
/
σ
n
)
−
e
−
t
2
s
k
2
/
2
σ
n
2
|
{\displaystyle \left|\varphi _{S_{n}/\sigma _{n}}(t)-e^{-t^{2}/2}\right|=\left|\prod _{k=1}^{n}\varphi _{X_{k}}(t/\sigma _{n})-\prod _{k=1}^{n}e^{-t^{2}s_{k}^{2}/2\sigma _{n}^{2}}\right|\leq \sum _{k=1}^{n}\left|\varphi _{X_{k}}(t/\sigma _{n})-e^{-t^{2}s_{k}^{2}/2\sigma _{n}^{2}}\right|}
泰勒展開，上式可近似為
∑
k
=
1
n
|
i
3
t
3
E
[
X
k
3
]
6
σ
n
3
+
t
4
s
k
4
8
σ
n
4
|
≤
|
t
|
3
6
σ
n
3
∑
k
=
1
n
E
[
|
X
k
|
3
]
+
t
4
8
σ
n
4
∑
k
=
1
n
s
k
4
≤
|
t
|
3
6
σ
n
3
∑
k
=
1
n
E
[
|
X
k
|
3
]
+
t
4
8
max
1
≤
k
≤
n
s
k
2
σ
n
2
{\displaystyle \sum _{k=1}^{n}\left|{\frac {i^{3}t^{3}E[X_{k}^{3}]}{6\sigma _{n}^{3}}}+{\frac {t^{4}s_{k}^{4}}{8\sigma _{n}^{4}}}\right|\leq {|t|^{3} \over 6\sigma _{n}^{3}}\sum _{k=1}^{n}E[|X_{k}|^{3}]+{\frac {t^{4}}{8\sigma _{n}^{4}}}\sum _{k=1}^{n}s_{k}^{4}\leq {|t|^{3} \over 6\sigma _{n}^{3}}\sum _{k=1}^{n}E[|X_{k}|^{3}]+{\frac {t^{4}}{8}}\max _{1\leq k\leq n}{s_{k}^{2} \over \sigma _{n}^{2}}}
由李亞普諾夫條件，當
n
→
∞
{\displaystyle n\rightarrow \infty }
令
k
n
=
a
r
g
max
1
≤
k
≤
n
s
k
2
/
σ
n
2
{\displaystyle k_{n}={\rm {arg}}\max _{1\leq k\leq n}s_{k}^{2}/\sigma _{n}^{2}}
李亞普諾夫不等式 ，
(
s
k
n
/
σ
n
)
3
/
2
≤
E
[
|
X
k
n
/
σ
n
|
3
]
≤
1
σ
n
3
∑
k
=
1
n
E
[
|
X
k
|
3
]
{\displaystyle (s_{k_{n}}/\sigma _{n})^{3/2}\leq E[|X_{k_{n}}/\sigma _{n}|^{3}]\leq {\frac {1}{\sigma _{n}^{3}}}\sum _{k=1}^{n}E[|X_{k}|^{3}]}
因此第二項也收斂於零。
證畢。
中央極限定理指出，隨著隨機變數數量的增加，許多具有有限變異數的獨立的且相同分布的隨機變數的總和將趨於常態分布。
李賢平，機率論基礎（第二版），高等教育出版社
Olav Kallenberg，現代機率論基礎（第二版），Springer（2002）。 
_-_Galton_1889_diagram.png)
![{\displaystyle [a,b]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle {\left[\varphi {\left({\frac {t}{\sigma {\sqrt {n}}}}\right)}\right]}^{n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e1c708fe0b820e2956c94ea910d451c138d37376)
![{\displaystyle {\left[\varphi {\left({\frac {t}{\sigma {\sqrt {n}}}}\right)}\right]}^{n}=\left[1-{\frac {1}{2n}}t^{2}+o\left({\frac {t^{2}}{n}}\right)\right]^{n}\to {e^{-t^{2}/2}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/645c2fce894b70d410d8a2d0afc4e10da54da156)
![{\displaystyle E[X_{i}]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f4c9e03e40d46499fafe6c167817d5fd76abbcc2)
![{\displaystyle \lim _{n\rightarrow \infty }{1 \over \sigma _{n}^{2}}\sum _{i=1}^{n}E[X_{i}^{2};\{|X_{i}|>\epsilon \sigma _{n}\}]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0297ae5e465b762cbf3a71e15d7d2e1619d1e113)
![{\displaystyle E[|X_{i}|^{3}]<\infty ,\,\lim _{n\rightarrow \infty }{1 \over \sigma _{n}^{3}}\sum _{i=1}^{n}E[|X_{i}|^{3}]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c855daeefe17ab4f3992cd776c0a805d8c3f5b7f)
![{\displaystyle \sum _{k=1}^{n}\left|{\frac {i^{3}t^{3}E[X_{k}^{3}]}{6\sigma _{n}^{3}}}+{\frac {t^{4}s_{k}^{4}}{8\sigma _{n}^{4}}}\right|\leq {|t|^{3} \over 6\sigma _{n}^{3}}\sum _{k=1}^{n}E[|X_{k}|^{3}]+{\frac {t^{4}}{8\sigma _{n}^{4}}}\sum _{k=1}^{n}s_{k}^{4}\leq {|t|^{3} \over 6\sigma _{n}^{3}}\sum _{k=1}^{n}E[|X_{k}|^{3}]+{\frac {t^{4}}{8}}\max _{1\leq k\leq n}{s_{k}^{2} \over \sigma _{n}^{2}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3dba085e636aefcd28ff7be53420a19d4e7c0889)
![{\displaystyle (s_{k_{n}}/\sigma _{n})^{3/2}\leq E[|X_{k_{n}}/\sigma _{n}|^{3}]\leq {\frac {1}{\sigma _{n}^{3}}}\sum _{k=1}^{n}E[|X_{k}|^{3}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/da8f7a389c3b84d646b8fda3117d7ccc135a8b38)
