循環群

在群論中，循環群（英文：cyclic group），是指能由單個元素所生成的群。有限循環群同構於整數同餘加法群 ${\displaystyle \mathbb {Z} {\big /}n\mathbb {Z} }$，無限循環群則同構於整數加法群。每個循環群都是阿貝爾群，亦即其運算是可交換的。在群論中，循環群的性質已經被研究的較為透徹，是更為複雜的代數研究中常用到的基礎工具。

群論
群
基本概念 子群 · 正規子群 · 商群 · 群同態 · 像 · (半)直積 · 直和 單純群 · 有限群 · 無限群 · 拓撲群 · 群概形 · 循環群 · 冪零群 · 可解群 · 圈積 離散群 有限單群分類 循環群 Zn 交錯群 An 李型群 散在群 馬蒂厄群 M11..12,M22..24 康威群 Co1..3 揚科群 J1..4 費歇爾群（英語：Fischer group）F22..24 子魔群（英語：sub monster group） B 魔群 M 其他有限群 對稱群, Sn 二面體群, Dn 無限群 整數, Z 模群, PSL(2,Z) 和 SL(2,Z) 連續群 李群 一般線性群 GL(n) 特殊線性群 SL(n) 正交群 O(n) 特殊正交群 SO(n) 么正群 U(n) 特殊么正群 SU(n) 辛群 Sp(n) G2 F4 E6 E7 E8 勞侖茲群 龐加萊群 無限維群 共形群 微分同胚群 環路群 量子群 O(∞) SU(∞) Sp(∞) 代數群 橢圓曲線 線性代數群（英語：Linear algebraic group） 阿貝爾簇（英語：Abelian variety）
閱 論 編

定義

6次單位根在乘法下形成循環群。z是本原元而 z² 不是，因為z的奇數次冪不是z²的冪。

設 ${\displaystyle (G,\cdot )}$ 為一個群，若存在一個元素 ${\displaystyle g\in G}$，使得 ${\displaystyle G=\left\langle \,g\,\right\rangle =\left\{g^{k}|\;k\in \mathbb {Z} \right\}}$，則 ${\displaystyle (G,\cdot )}$ 形成一個循環群。群 ${\displaystyle G}$ 內任意一個元素所生成的群都是循環群，而且是 ${\displaystyle G}$ 的子群。

分類

令循環群 ${\displaystyle G=\left\{g^{k}|\;k\in \mathbb {Z} \right\}}$。如果存在兩個相異整數 ${\displaystyle m,n}$ 使得 ${\displaystyle g^{m}=g^{n}}$，那麼 ${\displaystyle d=\vert m-n\vert }$ 滿足 ${\displaystyle g^{d}=e}$，其中 ${\displaystyle e}$ 是單位元素。所以對於任意整數 ${\displaystyle k}$，${\displaystyle g^{k}=g^{r}}$，其中 ${\displaystyle r}$ 是 ${\displaystyle k}$ 除以 ${\displaystyle d}$ 得到的餘數，${\displaystyle 0\leq r\leq d-1}$。這說明 ${\displaystyle G}$ 是有限群。設 ${\displaystyle d_{m}}$ 是所有這樣的正整數中最小的一個，則 ${\displaystyle G}$ 可以表示為：

${\displaystyle G=\left\{g^{k}|\;k=0,1,\ldots ,d_{m}-1\right\}}$

可以證明它同構於模 ${\displaystyle d_{m}}$ 的加法群 ${\displaystyle \left(\mathbb {Z} {\big /}d_{m}\mathbb {Z} ,+\right)}$。事實上，對每一個正整數 ${\displaystyle n}$，都存在唯一一個（在同構的意義上）階為此正整數 ${\displaystyle n}$ 的循環群。而所有的 ${\displaystyle n}$ 階循環群都和模 ${\displaystyle n}$ 的同餘類構成的加法群 ${\displaystyle \left(\mathbb {Z} {\big /}n\mathbb {Z} ,+\right)}$ 同構。如果一個循環群的階是無限的，那麼它同構於整數關於加法構成的群 ${\displaystyle \left(\mathbb {Z} ,+\right)}$。因此，循環群已被完全分類，是最簡單的一種群。

例如，${\displaystyle G=\left\{e,g,g^{2},g^{3},g^{4},g^{5}\right\}}$，則 ${\displaystyle G}$ 為循環群。${\displaystyle G}$ 同構於模 ${\displaystyle 6}$ 的加法群：${\displaystyle \mathbb {Z} _{6}=\left\{{\overline {0}},{\overline {1}},{\overline {2}},{\overline {3}},{\overline {4}},{\overline {5}}\right\}}$。考慮映射：

${\displaystyle \varphi :\;G\longrightarrow \mathbb {Z} _{6}}$

${\displaystyle \left.\;\,\right.g^{k}\,\mapsto \;\,{\overline {k}}}$

可以證明其為群同態，而且是對射，因此是群同構。

標記

由於循環群必然是阿貝爾群，且與加法群 ${\displaystyle \mathbb {Z} {\big /}n\mathbb {Z} }$ 或整數的加法群 ${\displaystyle \mathbb {Z} }$ 同構，它的運算常以加法表示並記為 ${\displaystyle \mathbb {Z} _{n}}$。然而數論中一般會避免使用這種標記，因為它和p進整數構成的環或群的局部化的標記相衝突，容易混淆。因此，數論中一般直接記作 ${\displaystyle \mathbb {Z} {\big /}n\mathbb {Z} }$，或以乘法表示運算並記為 ${\displaystyle C_{n}}$。

性質

每一個循環群要麼同構於整數模 ${\displaystyle n}$ 的加法群：${\displaystyle \mathbb {Z} _{n}=\left\{{\overline {0}},{\overline {1}},{\overline {2}},\cdots ,{\overline {n-1}}\right\}}$，要麼同構於整數的加法群 ${\displaystyle \mathbb {Z} }$。因此要研究循環群的性質，只需要研究 ${\displaystyle \mathbb {Z} _{n}}$和 ${\displaystyle \mathbb {Z} }$ 作為加法群的性質即可。設 ${\displaystyle G}$ 是一個 ${\displaystyle n}$ 階的循環群^{[N 1]}，${\displaystyle g\in G}$，則：

• ${\displaystyle G}$ 為交換群。這是因為 ${\displaystyle g+h\equiv h+g{\pmod {n}}}$ 。
• 若 ${\displaystyle n}$ 為正整數，則 ${\displaystyle g^{n}=e}$，因為${\displaystyle n\equiv 0{\pmod {n}}}$ 。而且 ${\displaystyle n}$ 是所有使得 ${\displaystyle g^{k}=e}$ 的正整數 ${\displaystyle k}$ 中最小的一個。
• 若 ${\displaystyle n}$ 為無限大，則 ${\displaystyle G}$ 有且僅有兩個生成元，分別對應於整數中的 ${\displaystyle 1}$ 和 ${\displaystyle -1}$。
• 若 ${\displaystyle n}$ 為正整數，則 ${\displaystyle G}$ 的各個生成元分別對應整數模 ${\displaystyle n}$ 加法群中與 ${\displaystyle n}$ 互質的數的同餘類。例如當 ${\displaystyle n=12}$ 時，${\displaystyle G}$ 的生成元有四個，分別對應著 ${\displaystyle \mathbb {Z} _{12}}$ 中的${\displaystyle {\overline {1}},{\overline {5}},{\overline {7}},{\overline {11}}}$四個同餘類。
• ${\displaystyle G}$ 的每一個子群都是循環群。每一個 ${\displaystyle G}$ 的 ${\displaystyle m}$ 階有限子群皆為整數模 ${\displaystyle m}$ 的加法群。而每一個 ${\displaystyle G}$ 的無限子群都可以表示成 ${\displaystyle m\mathbb {Z} }$，同構於 ${\displaystyle \mathbb {Z} }$。
• 設 ${\displaystyle p}$ 是質數，則階為 ${\displaystyle p}$ 的群都同構於 ${\displaystyle p}$ 階循環群。
• 兩個循環群的直積 ${\displaystyle \mathbb {Z} _{n}\times \mathbb {Z} _{m}}$是循環群若且唯若 ${\displaystyle n}$ 和 ${\displaystyle m}$ 互質。故 ${\displaystyle \mathbb {Z} _{12}}$ 同構於 ${\displaystyle \mathbb {Z} _{3}\times \mathbb {Z} _{4}}$，而不是 ${\displaystyle \mathbb {Z} _{2}\times \mathbb {Z} _{6}}$^{[N 2]}。
• 阿貝爾群的基本定理說明每一個有限生成阿貝爾群都是有限多個循環群的直積。

例子

在二維和三維空間裡，${\displaystyle n}$ 折旋轉對稱的對稱群為 ${\displaystyle C_{n}}$，屬 ${\displaystyle \mathbb {Z} _{n}}$ 抽象群類型。在三維裡，亦存在其他代數地相同的對稱群，詳見三維點群。

需留意的是，圓的所有旋轉所組成之群S¹(圓群)不是循環的，甚至不是可數的。

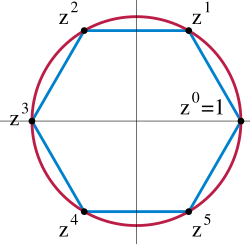
• ${\displaystyle n}$ 次單位根形成一個關於乘法的 ${\displaystyle n}$ 階循環群。

• 每一個有限體之有限擴張的伽羅瓦群是有限且循環的；相反地，給定一有限體F和一有限循環群 ${\displaystyle G}$，則存在一個 ${\displaystyle F}$ 的有限體擴張，其伽羅瓦群為 ${\displaystyle G}$。

表示

有限循環群的環圖全是有著其元素在各個角上的 ${\displaystyle n}$ 邊形。下面環圖中的黑角表示是單位元素，而其他的角則為群的其他元素。一個環包括著連接著單位元素之元素的接續之次方。

Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8

子群

所有循環群的子群及商群都是循環群。特別地，${\displaystyle \mathbb {Z} }$ 的子群為 ${\displaystyle m\mathbb {Z} }$ 的形式，其中 ${\displaystyle m}$ 為非負整數。對於不同的 ${\displaystyle m}$ ，形如 ${\displaystyle m\mathbb {Z} }$ 的子群都不同，且除了平凡群（${\displaystyle m=0}$）外都同構於 ${\displaystyle \mathbb {Z} }$ 。 ${\displaystyle \mathbb {Z} }$ 的子群格同構於以可除性排序之自然數格的對偶。除了一個平凡的反例 ${\displaystyle \mathbb {Z} \backslash \{0\}}$ 外， ${\displaystyle \mathbb {Z} }$ 的所有商群都是有限的。對每個 ${\displaystyle n}$ 的正因數 ${\displaystyle d}$ ，群 ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$ 恰有一個元質數目為 ${\displaystyle d}$ 的子群，它由 ${\displaystyle n/d}$ 的剩餘類所產生。其不存在其他的子群。故其子群格會同構於以可除性排序之 ${\displaystyle n}$ 的因數所組成的集合。

特別地，一個循環群是單群若且唯若其元質數目為質數。

舉一個實際的問題，給定一個 ${\displaystyle n}$ 目之有限子群 ${\displaystyle C}$，其生成元為 ${\displaystyle g}$，並要求求得以某一整數 ${\displaystyle k}$ 之 ${\displaystyle g^{k}}$ 所生成的子群之大小 ${\displaystyle m}$。這裡，${\displaystyle m}$ 會是能使 ${\displaystyle mk}$ 能被 ${\displaystyle n}$ 整除之最小正整數。因此其為 ${\displaystyle n/t}$，其中 ${\displaystyle t}$ 為 ${\displaystyle k}$ 和 ${\displaystyle n}$ 的最大公因數。換句話說，由 ${\displaystyle g^{k}}$ 產生之子群之指標為 ${\displaystyle t}$。其理由在數論中被稱為指標計算演算法。

自同態

阿貝爾群 ${\displaystyle \mathbb {Z} _{n}}$ 的自同態環會同構於此阿貝爾群，且使其構成一個環。在此同構之下，數字 ${\displaystyle r}$ 會對應於將每個元素映射至其 ${\displaystyle n}$ 次乘積之值上之 ${\displaystyle \mathbb {Z} _{n}}$ 的自同態。此一自同態只有在r和n互質時會是個對射函數，所以 ${\displaystyle \mathbb {Z} _{n}}$ 的自同構群會同構於群 ${\displaystyle \mathbb {Z} _{n}^{\times }}$(見上面)。${\displaystyle \mathbb {Z} _{n}}$ 的自同構群有時會被稱為 ${\displaystyle \mathbb {Z} _{n}}$ 的特徵群，且此一群的建構會直接導致對狄利克雷特徵的定義。

相似地，加法群 ${\displaystyle \mathbb {Z} }$ 的自同態環會同構於環 ${\displaystyle \mathbb {Z} }$ ，且其自同構群會同構於環 ${\displaystyle \mathbb {Z} }$ 的單位群，即${\displaystyle \{-1,+1\}\cong \mathbb {Z} _{2}}$。

逼肖循環群

一個群稱為逼肖循環（virtually cyclic）的，如果這個群包含一個有限指數的循環子群。換言之，一個逼肖循環群的任何元素，都可表示為這個循環子群的一個元素乘以群中某個有限子集的一個元素。一個無限群是逼肖循環的，若且唯若這個群是有限生成並且正好有兩個端。^[1]逼肖循環群的一個簡單例子是 ${\displaystyle \mathbb {Z} /n}$ 和 ${\displaystyle \mathbb {Z} }$ 的直積，因子 ${\displaystyle \mathbb {Z} }$ 有有限指數 ${\displaystyle n}$。任何格羅莫夫雙曲群的阿貝爾子群都是逼肖循環群。^[2]

注釋

1. n也可以是無限大，約定「n為無窮大」代表群同構於整數加法群。
2. ${\displaystyle \mathbb {Z} _{2}}$和${\displaystyle \mathbb {Z} _{6}}$的直積並不是一個循環群。

參考來源

1. Stallings, John, Groups of cohomological dimension one, Applications of Categorical Algebra (Proc. Sympos. Pure Math., Vol. XVIII, New York, 1968), Providence, R.I.: Amer. Math. Soc.: 124–128, 1970, MR 0255689. 特別見p. 126: "If G has two ends, the explicit structure of G is well known: G is an extension of a finite group by either the infinite cyclic group or the infinite dihedral group."
2. Alonso, J. M.; Brady, T.; Cooper, D.; Ferlini, V.; Lustig, M.; Mihalik, M.; Shapiro, M.; Short, H., Notes on word hyperbolic groups, Group theory from a geometrical viewpoint (Trieste, 1990) (PDF), River Edge, NJ: World Scientific, Corollary 3.6, 1991 [2014-04-01], MR 1170363, （原始內容 (PDF)存檔於2013-04-25）

相關文獻

• Gallian, Joseph, Contemporary abstract algebra 4th, Boston: Houghton Mifflin, 1998, ISBN 978-0-669-86179-2 （英語）, especially chapter 4.
• Herstein, I. N., Abstract algebra 3rd, Prentice Hall, 1996, ISBN 978-0-13-374562-7, MR1375019, especially pages 53–60.

另見

• 三維循環對稱群
• 循環擴張
• 循環模
• 同餘