病态 (数学)

在数学中，病态（英语：Pathological）现象是指其性质被认为是非典型的或反直觉的现象，反义词为良态（Well-behaved）。

魏尔斯特拉斯函数是无处不连续的，但任何一处都不可微

在分析学中

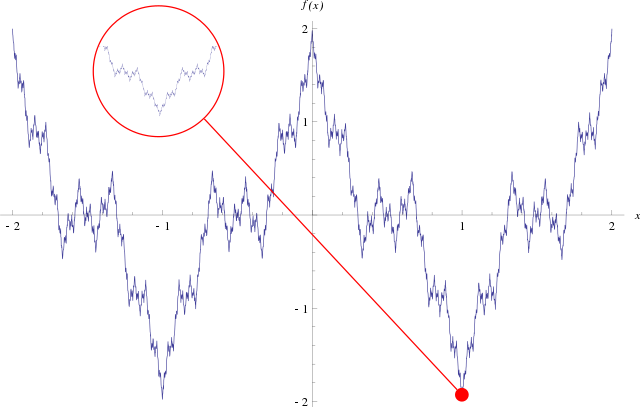
一个经典的例子的病态结构是魏尔斯特拉斯函数，它处处连续但处处不可微。可微函数和魏尔斯特拉斯函数的总和也是连续的，但是无处可微；所以这种函数至少与可微函数一样多。事实上，由贝尔纲定理之一可以显示，连续函数通常是无处可微的。

通俗地说，大多数函数都不可微，而且相对较少的函数可以被描述或研究。一般而言，大多数实用的函数也具有某种物理基础或实际应用，这意味着它们在理论数学或逻辑层面上不能是病态的；如果没有像狄拉克δ函数那样的某些限制性情况，它们往往表现得非常正态，直观。引用庞加莱的话：

有时，逻辑生出妖怪。近半世纪，怪诞的函数异军突起，竭力标奇立异，与实际有用的函数大相径庭。其不再连续，甚或连续但不可导，如此种种。诚然，以逻辑观之，该等怪异函数才是最普遍；相反，以简单法则定义，无需刻意寻找的函数，反倒是特例，仅占墙隅立锥之地。

以前，发明新函数，是为实用；今时，则祗为刻意突显先贤的逻辑缺陷，此外别无他用。

师者若祗以逻辑为纲领，则必由最普遍的函数开始教授，亦即最怪异的函数。如此，学生初学已须勉强面对整座畸形学博物馆（musée tératologique）；否则，逻辑学家会挑剔你仅逐步迈向严谨。

——Henri Poincaré^[1]，1899

这突出表明，该术语“病态”是主观的，依赖于语境，并且正在逐渐消失。它在任何特定情况下的含义都存在于数学家群体中，而不一定在数学本身中。此外，引文显示数学经常如何通过反例进展到直觉或预期结果；例如所提到的“不可导”与目前对太阳等离子体中磁重联事件的研究密切相关。

在拓扑学中

拓扑学中最臭名昭着的病态之一是亚历山大带角球（英语：Alexander horned sphere），这是一个反例，表明拓扑将球体S²嵌入R³中可能无法完全分离空间。作为反例，它激发了驯服（tameness）的额外条件，这抑制了带角球所表现出的野性行为。

像许多其他病态一样，带角球在某种意义上是无限精细的递归生成结构，在极限情况下违反了普通的直觉。在这种情况下，在极限范围内连续的球体互锁环的不断下降的链的拓扑结构完全反映了普通球体的拓扑结构，而期望在嵌入之后它的外部表现相同。然而事实却并非如此：它没有单连通。

对于基础理论，请参阅乔登-薛弗利斯定理（英语：Schoenflies problem）。

在线性代数中

定义：如果线性方程组${\displaystyle Ax=b}$ 中，A或b的元素的微小变化，会引起方程组解的巨大变化，则称方程组为病态方程组，称矩阵A为病态矩阵。条件数可以用来衡量方程组的“病态”程度。^[2]

一种常见的病态矩阵是n阶希尔伯特矩阵，随着阶数n的增大，而呈现严重的病态。^[2]

良态

数学家（以及相关科学家）经常谈论一个数学对象（函数、集合，或任何空间）是否良态。该术语没有固定的正式定义，而是取决于背景、数学兴趣、时尚和品味。为了确保对象处在良态，数学家引入了进一步的公理来缩小研究领域。这有利于使分析更容易，但减少了所得结论的一般性。像非欧几何这样的概念曾被认为是不正常的，但现在已成为常见的研究对象。

在纯数学和应用数学（例如最优化、数值积分或数学物理学）中，良态也意味着研究对象满足目前分析适用所需的一切假设。

相反的情况通常标记为病态的。在（基数或测度意义下）大多数例子中，这种病态情况并不罕见，但除非故意构建，否则病态情况不会在实践中出现。

术语“表现良好”（或良态）通常用于绝对意义上——要么表现得好，要么反之。例如：

• 在算法推理（英语：Algorithmic inference）中，表现良好的统计量（英语：Well-behaved statistic）是单调的、明确定义的和充分的。
• 在裴蜀定理中，如果两个多项式的多项式最大公约数是常数，它们的交点数定理给出的公式是有效的，它们表现良好。
• 亚纯函数是两个表现良好的函数的比，指的是这两个函数是全纯的。
• 卡罗需－库恩－塔克条件是一个表现良好的非线性规划问题解决方案最优的一阶必要条件；如果满足一些规律性条件，则问题被称为表现良好。
• 在概率上，概率空间对应的Σ-代数中包含的事件表现良好，可测函数也是如此。

虽然较少见，但该术语也可以比较方式使用：

• 在微积分中：
  • 解析函数比一般光滑函数表现得更好。
  • 平滑函数比一般可微函数表现更好。
  • 连续可微函数比一般连续函数表现更好。函数可以微分的次数越多，它的表现就越好。
  • 连续函数比稠密集上的黎曼可积函数表现更好。
  • 黎曼可积函数比勒贝格可积函数表现更好。
  • 勒贝格可积函数比一般函数表现更好。
• 在拓扑中，连续函数比不连续函数表现得更好。
  • 欧几里德空间比非欧几里德几何更好。
  • 吸引不动点比排斥不动点更好。
  • 豪斯多夫空间比任意点集拓扑中的拓扑更好。
  • 博雷尔集比任意实数集合表现更好。
  • 具有整数维度的空间比具有分形维度的空间表现得更好。
• 在抽象代数中：
  • 群比原群和半群更好。
  • 阿贝尔群表现得比非阿贝尔群更好。
  • 有限生成阿贝尔群比非有限生成交换群表现更好。
  • 有限维向量空间比无限维向量空间更好。
  • 域比除环或一般环更好。
  • 可分离的域扩张比不可分离的域扩张更好。
  • 赋范除法代数比一般组合代数表现得更好。

病态实例

病态的实例通常具有一些不合乎需要或不寻常的特性，所以难以在理论中包含或解释。这种病态行为常常引发新的研究，从而产生新的理论和更一般的结果。例如，一些重要的历史例子如下：

• 古希腊毕达哥拉斯学派发现的无理数；例如，单位正方形的对角线的长度，即${\displaystyle {\sqrt {2}}}$。
• 有理数的基数等于整数的基数。
• 某些代数数域的整数环无唯一分解，例如域${\textstyle \mathbb {Q} ({\sqrt {-5}})}$。
• 分形和其他“粗糙”几何对象的发现（参见豪斯多夫维数）。
• 魏尔施特拉斯函数，一个在实直线上的实数值函数，它在任何地方都是连续的，但在任何地方都不是可微分的。
• 实际分析和分布理论中的测试函数，它们是实直线上的无限可微函数，在给定的有限区间之外的任何地方都是0。这种函数的一个例子是测试函数，${\textstyle \varphi (t)={\begin{cases}e^{-1/(1-t^{2})},&{\text{若 }}-1<t<1,\\0,&{\text{其 他 情 況 }}\ \ .\end{cases}}}$
• 康托尔集是区间[0, 1]的零测度子集，但不可数。
• 皮亚诺曲线是一个将区间[0, 1]映射到[0, 1] × [0, 1]的连续的满射函数。
• 有理数的指标函数有界但处处不连续，且不是黎曼可积的。
• 康托尔函数是一个单调的连续映射，它将[0,1]映射到[0,1]，但几乎处处导数为零。
• 可以为皮亚诺算术的可数递归饱和模型构建包含满足“直观错误”算术语句的类。^{[来源请求]}

在它们被发现时，这些实例被认为是高度病态的；今天，每个实例都被同化为现代数学理论了。这些例子促使他们的观察者纠正他们的信仰或直觉；有时他们甚至可能需要重新评估基本定义和概念。在历史的过程中，它们导致了更正确，更精确，更强大的数学。例如，狄利克雷函数是勒贝格可积的，而测试函数的卷积适用于求出任何局部可积函数的平滑拟合（此处拟合是在局部可积函数的空间中，几乎处处意义下）。

根据定义，行为是否是病态的，取决于个人的直觉。病态依赖于背景、培训和经验——一个研究人员看来是病态，很可能另一个人看来表现良好。

病态的例子可以说明假设在一个定理中的重要性。例如，在统计学中，即使柯西分布的对称钟形看起来与许多分布相似，它也不满足中心极限定理；其平均值和标准偏差不存在（或非有限），所以不满足定理的假设。

一些最著名的悖论如巴拿赫-塔斯基悖论和豪斯多夫悖论都基于不可测集的存在性。除非他们采取少数立场否认选择公理，不然数学家一般都只能接受这些集合存在。^{[来源请求]}

计算机科学

在计算机科学中，“病态”对算法的研究略有不同。这里，如果输入（或输入集合）引起来自算法的非典型行为，例如违反其平均情况复杂性或甚至其正确性，则称输入（或输入集合）是病态的。例如，哈希表通常具有病态输入：在哈希值上碰撞的键组。快速排序通常具有O(n log n)时间复杂度，但是当给定输入触发次优行为时恶化为O(n² )。

这个术语经常作为一种拒绝输入的方式作贬义使用，例如被专门设计来打破一个在实践中听起来很正常的惯例（与拜占庭将军问题比较）。另一方面，对病态输入的认识很重要，因为它们可被利用来对计算机系统进行拒绝服务攻击。此外，这个意义上的术语与其他意义一样是主观判断的问题。如果有足够的运行时间，足够大和多样化的用户群或其他因素，实际上可能会发生可被视为病态的输入（如在亚利安5号的第一次试飞中所见）。

特殊情况

一个类似但不同的现象是特殊对象（和异常的同构），当一般模式存在“少量”例外时——一定量地，对于无限规则的有限的例外集合。相比之下，在病态的情况下，通常大多数或几乎所有的现象都是病态的，如普遍存在的那样，例如几乎所有的实数都是无理数。

主观上，特殊情况（例如二十面体或散在群）通常被认为是“美丽的”，一个理论的意外例子。而病态现象顾名思义通常被认为是“丑陋的”。因此，理论通常扩展到包括特殊对象——例如，单李代数被包含在半单李代数理论中：公理被认为是好的，特殊对象是意外但有效的。相比之下，病态的例子被用来指出公理中的一个缺点，需要更强的公理来排除它们 - 例如，要求在Schönflies问题中嵌入球体的驯化。人们可以研究更一般的理论，包括可以提供其自身简化的病态（实数具有与有理数非常不同的属性，同样连续映射具有与平滑映射非常不同的属性），但也将在一般情况下研究狭义的理论，从中得出原始的例子。

参考文献

1. Poincaré, Henri. Science et méthode. 1908: 132–133 （法语）. La logique parfois engendre des monstres. On vit surgir toute une foule de fonctions bizarres qui semblaient s'efforcer de ressembler aussi peu que possible aux honnêtes fonctions qui servent à quelque chose. Plus de continuité, ou bien de la continuité, mais pas de dérivées etc. Bien plus, au point de vue logique, ce sont ces fonctions étranges qui sont les plus générales, celles qu'on rencontre sans les avoir cherchées n'apparaissent plus que comme un cas particulier. Il ne leur reste qu'un tout petit coin.

   Autrefois, quand on inventait une fonction nouvelle, c'était en vue de quelque but pratique; aujourd'hui, on les invente tout exprès pour mettre en défaut les raisonnements de nos pères, et on n'en tirera jamais que cela.

   Si la logique était le seul guide du pédagogue, ce serait par les fonctions les plus générales, c'est-à-dire parles plus bizarres, qu'il faudrait commencer. C'est le débutant qu'il faudrait mettre aux prises avec ce musée tératologique. Si vous ne le faites pas, pourraient dire les logiciens, vous n'atteindrez la rigueur que par étapes.

2. 张宏伟，金光日，施吉林，董波 (编). 计算机科学计算 2013年第2版. 北京: 高等教育出版社. 2005: 51–54. ISBN 9787040365955.

外部链接

• 病态结构和分形（页面存档备份，存于互联网档案馆） ，引用自弗里曼·戴森的一篇文章，"Characterising Irregularity"，《科学》，1978年5月

本条目含有来自PlanetMath《pathological》的内容，版权遵守知识共享协议：署名-相同方式共享协议。