图论 (英语:Graph theory ),是组合数学 分支,和其他数学分支如群论 、矩阵论、拓扑学 有着密切关系。
一个由6个顶点和7条边组成的图 图 是图论的主要研究对象。图是由若干给定的顶点 及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物间具有这种关系。
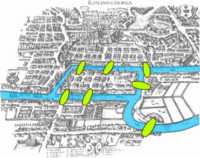
图论起源于著名的柯尼斯堡七桥问题 。该问题于1736年被欧拉 解决,因此普遍认为欧拉 是图论的创始人。[ 1]
图论的研究对象相当于一维的单纯复形 [ 2]
柯尼斯堡七桥问题 一般认为,欧拉 于1736年出版的关于柯尼斯堡七桥问题 的论文是图论领域的第一篇文章[ 3] 一笔画问题 。而此论文与范德蒙 的一篇关于骑士周游问题 的文章,则是继承了莱布尼茨 提出的“位置分析”的方法。欧拉提出的关于凸多边形顶点数、棱数及面数之间的关系的欧拉公式 与图论有密切联系,此后又被柯西 等人[ 4] [ 5] 拓扑学 的起源。1857年,哈密顿 发明了“环游世界游戏 哈密顿路径问题 ”。
西尔维斯特 于1878年发表在《自然 》上的一篇论文中首次提出“图”这一名词[ 6]
欧拉的论文发表后一个多世纪,凯莱 研究了在微分学 中出现的一种数学分析的特殊形式,而这最终将他引向对一种特殊的被称为“树 ”的图的研究。由于有机化学中有许多树状结构的分子,这些研究对于理论化学有着重要意义,尤其是其中关于具有某一特定性质的图的计数 问题。除凯莱的成果外,波利亚 也于1935至1937年发表了一些成果,1959年,De Bruijn
四色问题 可谓是图论研究史上最著名也是产生成果最多的问题之一:“是否任何一幅画在平面上的地图都可以用四种颜色染色,使得任意两个相邻的区域不同色?”这一问题由法兰西斯·古德里 于1852年提出,而最早的文字记载则出现在德摩根 于1852年写给哈密顿的一封信上。包括凯莱 、肯普 泰特 希伍德 、拉姆齐 和Hadwige 亏格 的曲面的图的着色问题的研究。一百多年后,四色问题仍未解决。1969年,Heinrich Heesch 凯尼斯·阿佩尔 和沃夫冈·哈肯 借助计算机给出了一个证明,此方法按某些性质将所有地图分为1936类并利用计算机一一验证了它们可以用四种颜色染色。但此方法由于过于复杂,在当时未被广泛接受。
1860年之1930年间,若当 、库拉托夫斯基 和惠特尼 从之前独立于图论发展的拓扑学中吸取大量内容进入图论,而现代代数方法的使用更让图论与拓扑走上共同发展的道路。其中应用代数较早者如物理学家基尔霍夫 于1845年发表的基尔霍夫电路定律 。
图论中概率方法的引入,尤其是埃尔德什 和Alfréd Rényi 随机图论 。
图论中有许多定义,以下是一些与之相关最基本的定义。
有三个边和三个顶点的图。 图论中,图 是有序对
G
=
(
V
,
E
)
{\displaystyle G=(V,E)}
V
{\displaystyle V}
E
⊆
{
{
x
,
y
}
:
(
x
,
y
)
∈
V
2
,
x
≠
y
}
{\displaystyle E\subseteq \left\{\left\{x,y\right\}:(x,y)\in V^{2},x\neq y\right\}}
{
x
,
y
}
{\displaystyle \left\{x,y\right\}}
x
,
y
{\displaystyle x,y}
为了避免歧异,上述的定义被更精准地称作无向简单图。
事实上可以推广为更一般的定义:图 是有序三元组
G
=
(
V
,
E
,
ϕ
)
{\displaystyle G=(V,E,\phi )}
V
{\displaystyle V}
E
{\displaystyle E}
E
{\displaystyle E}
ϕ
:
E
→
{
{
x
,
y
}
:
(
x
,
y
)
∈
V
2
}
{\displaystyle \phi :E\to \left\{\left\{x,y\right\}:(x,y)\in V^{2}\right\}}
为了避免歧异,上述的定义被更精准地称作无向图。
V
,
E
{\displaystyle V,E}
V
{\displaystyle V}
E
{\displaystyle E}
|
V
|
{\displaystyle |V|}
|
E
|
{\displaystyle |E|}
子图同构问题 :给定两个图
G
{\displaystyle G}
H
{\displaystyle H}
G
{\displaystyle G}
H
{\displaystyle H}
同构 。这是一个NP完全问题 。
哈密顿回路问题 可视为一个子图同构问题,即给定一个
n
{\displaystyle n}
n
{\displaystyle n}
一类相关的常见问题要求在给定图中寻找符合某些条件的最大子图,其中有很多是NP完全的,如:
类似地,有些问题要求寻找符合某些条件的最大导出子图,如:
最大独立集问题 :在给定图中寻找最大的无边的导出子图,亦即独立集 (NP完全)。平面图 判定:判定给定的图是否是平面图(此问题与子图的关系,参见库拉托夫斯基定理 )
一个尚未解决的与子图相关的猜想,重构猜想 (Reconstruction conjecture ):一个n 阶图是否能够由其所有n-1 阶导出子图唯一确定?
点色数 (Chromatic number )边色数 (Chromatic index )色多项式 许多问题与将图以特定方式染色 有关,如:
四色问题 完美图问题 (strong perfect graph theorem )列表染色问题,列表边染色问题
曲面染色
卜月华; 吴建专; 顾国华; 殷翔, 《图论及其应用》 第一版, 东南大学出版社: 1-2, 2007
Biggs, N.; Lloyd, E.; Wilson, R., Graph Theory, 1736–1936, Oxford University Press, 1986
Cauchy, A. L., Recherche sur les polyèdres - premier mémoire, Journal de l'École polytechnique, 1813,, 9 (Cahier 16): 66–86.
L'Huillier, S.-A.-J., Mémoire sur la polyèdrométrie, Annales de Mathématiques, 1812–1813, 3 : 169–189.
Berge, Claude , Théorie des graphes et ses applications, Collection Universitaire de Mathématiques II , Paris: Dunod, 1958Biggs, N.; Lloyd, E.; Wilson, R., Graph Theory, 1736–1936, Oxford University Press, 1986 .Bondy, J.A.; Murty, U.S.R., Graph Theory, Springer, 2008, ISBN 978-1-84628-969-9 .Bondy, Riordan, O.M, Mathematical results on scale-free random graphs in "Handbook of Graphs and Networks" (S. Bornholdt and H.G. Schuster (eds)), Wiley VCH, Weinheim, 1st ed., 2003 .Chartrand, Gary , Introductory Graph Theory, Dover, 1985, ISBN 0-486-24775-9Gibbons, Alan, Algorithmic Graph Theory, Cambridge University Press , 1985 .Reuven Cohen, Shlomo Havlin, Complex Networks: Structure, Robustness and Function, Cambridge University Press, 2010 Golumbic, Martin , Algorithmic Graph Theory and Perfect Graphs, Academic Press , 1980Harary, Frank , Graph Theory, Reading, MA: Addison-Wesley, 1969Harary, Frank ; Palmer, Edgar M., Graphical Enumeration, New York, NY: Academic Press, 1973Mahadev, N.V.R.; Peled, Uri N., Threshold Graphs and Related Topics, North-Holland , 1995 .Mark Newman, Networks: An Introduction, Oxford University Press, 2010 .