单峰

数学中，单峰意味着拥有唯一的众数。更一般地说，单峰意味着数学对象只有唯一的最大值。^[1]

单峰概率分布

图 1. 正态分布的概率密度函数，单峰分布的例子。

图 2. 简单双峰分布。

图 3. 双峰分布。注意只有最大的峰才对应严格的峰定义。

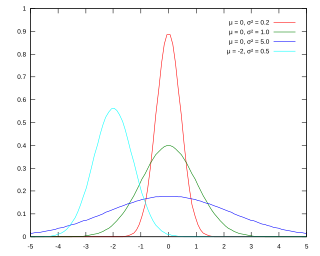
统计学中，单峰概率分布或单峰分布是具有单一峰值的概率分布。“峰”指分布的任何峰值，不仅仅是统计学中通常的众数。

若只有一个峰，则分布函数就是“单峰”的。除此之外都叫做“多峰”（multimodal）。^[2]图 1展示的正态分布、柯西分布、T分布、卡方分布、指数分布等都是单峰分布。离散型分布中，二项分布和泊松分布可视作单峰分布，但对于某些参数可以在两个相邻值上产生相同的概率。

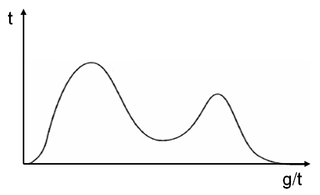
图 2、图 3展示了双峰分布。

其他定义

分布函数的单峰性还有其他定义。

对于连续型分布，单峰性可通过累积分布函数（CDF）的行为定义。^[3]若CDF在${\displaystyle x<m}$时是凸的、在${\displaystyle x<m}$时是凹的，则分布就是单峰分布，${\displaystyle m}$为众数。需要注意的是，根据这一定义，均匀分布也是单峰分布^[4]，任何在一定区间内可取到最大分布的也是单峰分布，如梯形分布。这一定义通常允许峰处不连续；在连续分布中，任意单一值的概率通常都是0，而这一定义则允许在峰中存在非零概率点。

单峰的标准也可用分布的特征函数^[3]或拉普拉斯-斯蒂尔切斯变换来定义。^[5]

定义单峰离散分布的另一种方法是通过概率差序列的变号。^[6]离散分布的概率质量函数为${\displaystyle \{p_{n}:n=\dots ,-1,0,1,\dots \}}$，若序列${\displaystyle \dots ,p_{-2}-p_{-1},p_{-1}-p_{0},p_{0}-p_{1},p_{1}-p_{2},\dots }$只有一次变号（不计入零），则称为单峰分布。

使用与结果

分布的单峰性之所以重要，是因为它可以得到几个重要的结果。下面给出的几个不等式仅适用于单峰分布，因此评估给定数据集是否来自单峰分布非常重要。双峰分布条目中给出了几种单峰测试法。

不等式

参见：切比雪夫不等式

高斯不等式

高斯不等式是第一个重要结果，^[7]给出了值与峰的距离超过给定数的概率的上限，其只能用于单峰分布。

维索尚斯基–佩图宁不等式

第二个是维索尚斯基–佩图宁不等式，^[8]其是切比雪夫不等式的细化。切比雪夫不等式保证在任何分布中，“几乎所有”值都“接近”均值。而维索尚斯基–佩图宁不等式则将其细化到更接近的值，前提是分布函数为连续单峰的。Sellke与Sellke得出了进一步的结果。^[9]

众数、中位数与平均数

高斯在1823年也证明了单峰分布的情形^[10]

${\displaystyle \sigma \leq \omega \leq 2\sigma }$

及

${\displaystyle |\nu -\mu |\leq {\sqrt {\frac {3}{4}}}\omega ,}$

其中中位数是ν，平均数是μ， ω是与众数的均方根误差。

对于单峰分布，可以证明中位数ν与平均值μ在(3/5)^1/2 ≈ 0.7746个标准差的范围内。^[11]用符号表示，

${\displaystyle {\frac {|\nu -\mu |}{\sigma }}\leq {\sqrt {\frac {3}{5}}}}$

其中| . |是绝对值。

2020年，Bernard、Kazzi与Vanduffel通过推导对称分位数均值${\displaystyle {\frac {q_{\alpha }+q_{(1-\alpha )}}{2}}}$与均值^[12]

${\displaystyle {\frac {\left|{\frac {q_{\alpha }+q_{(1-\alpha )}}{2}}-\mu \right|}{\sigma }}\leq \left\{{\begin{array}{cl}{\frac {{\sqrt[{}]{{\frac {4}{9(1-\alpha )}}-1}}{\text{ }}+{\text{ }}{\sqrt[{}]{\frac {1-\alpha }{1/3+\alpha }}}}{2}}&{\text{for }}\alpha \in \left[{\frac {5}{6}},1\right)\!,\\{\frac {{\sqrt[{}]{\frac {3\alpha }{4-3\alpha }}}{\text{ }}+{\text{ }}{\sqrt[{}]{\frac {1-\alpha }{1/3+\alpha }}}}{2}}&{\text{for }}\alpha \in \left({\frac {1}{6}},{\frac {5}{6}}\right)\!,\\{\frac {{\sqrt[{}]{\frac {3\alpha }{4-3\alpha }}}{\text{ }}+{\text{ }}{\sqrt[{}]{{\frac {4}{9\alpha }}-1}}}{2}}&{\text{for }}\alpha \in \left(0,{\frac {1}{6}}\right]\!.\end{array}}\right.}$

之间的最大距离，推广了前面的不等式。值得注意的是，${\displaystyle \alpha =0.5}$时最大距离取得最小（即当对称分位均值${\displaystyle =q_{0.5}=\nu }$），这也是选择中位数为均值的稳健估计值的原因之一。此外，当${\displaystyle \alpha =0.5}$，边界等于${\displaystyle {\sqrt {3/5}}}$，这时单峰分布中位数和均值距离的最大值。

中位数和众数θ也有类似关系：它们位于3^1/2 ≈ 1.732个标准差之内：

${\displaystyle {\frac {|\nu -\theta |}{\sigma }}\leq {\sqrt {3}}.}$

也可以证明均值和众数相差在3^1/2之内：

${\displaystyle {\frac {|\mu -\theta |}{\sigma }}\leq {\sqrt {3}}.}$

偏度与峰度

Rohatgi与Szekely声称，单峰分布的偏度与峰度可通过不等式相联系：^[13]

${\displaystyle \gamma ^{2}-\kappa \leq {\frac {6}{5}}=1.2}$

κ为峰度，γ为偏度。Klaassen、Mokveld与van Es发现，这只适于部分情形，如众数与均值重合的单峰分布集合。^[14]

他们推导出了一个适用于所有单峰分布的较弱不等式：^[14]

${\displaystyle \gamma ^{2}-\kappa \leq {\frac {186}{125}}=1.488}$

这个界限很锐，因为它是[0, 1]上的均匀分布和{0}处的离散分布的等权混合。

单峰函数

“峰”适用于数据集合概率分布，而非一般函数，所以上述定义并不适用。“单峰”的定义可扩展到实数函数。

通常定义如下：若对某值m，函数f(x)在${\displaystyle x\leq m}$时单调递增、在${\displaystyle x\geq m}$时单调递减，则为单峰函数。也就是说，f(x)的最大值为f(m)，且没有其他极大值。

证明单峰性通常很难。一种方法是利用定义，但这只适用于简单函数。还有基于导数的通用方法^[15]，但并不适用于每个函数。

单峰函数有二次项系数为负的二次函数、帐篷映射等等。

上述情形有时被称为强单调性。如有值m使${\displaystyle x\leq m}$时，函数f(x)弱单调递增；${\displaystyle x\geq m}$时，函数f(x)弱单调递减，则称函数为弱单峰函数。这时，x存在可取到最大值f(m)的区间。杨辉三角的每一行都是弱单峰函数。

单峰函数也可以指只有一个极小值的函数。^[16]例如，数值优化中的局部单峰抽样经常用这样的函数演示。可以说，这种推广下的单峰函数具有单一局部极值。

单峰函数的重要特性之一是，可以使用黄金分割搜索、三份查找或逐次抛物线插值等搜索算法找到最值。^[17]

其他推广

若${\displaystyle \forall x\neq c}$施瓦兹导数均为负，则函数f(x)是“S-单峰”（常称为“S-单峰映射”）函数，其中${\displaystyle c}$是临界点。^[18] 计算几何中，单峰函数可以设计出高效的找到极值的算法。^[19]

适用于向量自变量X的函数f(X)的更一般定义是，若存在可微单射X = G(Z)使f(G(Z))为凸函数，则f是单峰函数。通常，我们希望G(Z)连续可微，且有可逆雅各布矩阵。

拟凸函数和拟凹函数将单峰性推广到参数属于高维欧几里得空间的函数。

另见

• 双峰分布

参考文献

1. 埃里克·韦斯坦因. Unimodal. MathWorld.
2. 埃里克·韦斯坦因. Mode. MathWorld.
3. A.Ya. Khinchin. On unimodal distributions. Trams. Res. Inst. Math. Mech. (University of Tomsk). 1938, 2 (2): 1–7 （俄语）.
4. Ushakov, N.G., Unimodal distribution, Hazewinkel, Michiel (编), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
5. Vladimirovich Gnedenko and Victor Yu Korolev. Random summation: limit theorems and applications. CRC-Press. 1996. ISBN 0-8493-2875-6. p. 31
6. Medgyessy, P. On the unimodality of discrete distributions. Periodica Mathematica Hungarica. 1972-03, 2 (1–4): 245–257. S2CID 119817256. doi:10.1007/bf02018665.
7. Gauss, C. F. Theoria Combinationis Observationum Erroribus Minimis Obnoxiae, Pars Prior. Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores. 1823, 5.
8. D. F. Vysochanskij, Y. I. Petunin. Justification of the 3σ rule for unimodal distributions. Theory of Probability and Mathematical Statistics. 1980, 21: 25–36.
9. Sellke, T.M.; Sellke, S.H. Chebyshev inequalities for unimodal distributions. American Statistician (American Statistical Association). 1997, 51 (1): 34–40. JSTOR 2684690. doi:10.2307/2684690.
10. Gauss C.F. Theoria Combinationis Observationum Erroribus Minimis Obnoxiae. Pars Prior. Pars Posterior. Supplementum. Theory of the Combination of Observations Least Subject to Errors. Part One. Part Two. Supplement. 1995. Translated by G.W. Stewart. Classics in Applied Mathematics Series, Society for Industrial and Applied Mathematics, Philadelphia
11. Basu, S.; Dasgupta, A. The Mean, Median, and Mode of Unimodal Distributions: A Characterization. Theory of Probability & Its Applications. 1997, 41 (2): 210–223 [2023-09-24]. doi:10.1137/S0040585X97975447. （原始内容存档于2019-04-29）.
12. Bernard, Carole; Kazzi, Rodrigue; Vanduffel, Steven. Range Value-at-Risk bounds for unimodal distributions under partial information. Insurance: Mathematics and Economics. 2020, 94: 9–24. doi:10.1016/j.insmatheco.2020.05.013 .
13. Rohatgi, Vijay K.; Székely, Gábor J. Sharp inequalities between skewness and kurtosis. Statistics & Probability Letters. 1989, 8 (4): 297–299. doi:10.1016/0167-7152(89)90035-7.
14. Klaassen, Chris A.J.; Mokveld, Philip J.; Van Es, Bert. Squared skewness minus kurtosis bounded by 186/125 for unimodal distributions. Statistics & Probability Letters. 2000, 50 (2): 131–135. doi:10.1016/S0167-7152(00)00090-0.
15. On the unimodality of METRIC Approximation subject to normally distributed demands. (PDF). Method in appendix D, Example in theorem 2 page 5. [2013-08-28]. （原始内容存档 (PDF)于2017-08-09）.
16. Mathematical Programming Glossary.. [2020-03-29]. （原始内容存档于2022-03-28）.
17. Demaine, Erik D.; Langerman, Stefan. Optimizing a 2D Function Satisfying Unimodality Properties. Brodal, Gerth Stølting; Leonardi, Stefano (编). Algorithms – ESA 2005. Lecture Notes in Computer Science 3669. Berlin, Heidelberg: Springer. 2005: 887–898 [2023-09-24]. ISBN 978-3-540-31951-1. doi:10.1007/11561071_78. （原始内容存档于2023-07-09） （英语）.
18. See e.g. John Guckenheimer; Stewart Johnson. Distortion of S-Unimodal Maps. Annals of Mathematics. Second Series. July 1990, 132 (1): 71–130. JSTOR 1971501. doi:10.2307/1971501.
19. Godfried T. Toussaint. Complexity, convexity, and unimodality. International Journal of Computer and Information Sciences. June 1984, 13 (3): 197–217. S2CID 11577312. doi:10.1007/bf00979872.