正态分布

正态分布（normal distribution，中国大陆作正态分布，台湾作常态分布），物理学中通称高斯分布（Gaussian distribution）^[1]，是一个非常常见的连续概率分布。正态分布在统计学上十分重要，经常用在自然和社会科学来代表一个不明的随机变量。^[2][3]

正态分布

概率密度函数 红线代表标准正态分布
累积分布函数 颜色与概率密度函数相同
记号	${\displaystyle N(\mu ,\sigma ^{2})}$
参数	${\displaystyle \mu }$数学期望（实数） ${\displaystyle \sigma ^{2}>0}$方差（实数）
值域	${\displaystyle x\in (-\infty ;+\infty )\!}$
概率密度函数	${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)\!}$
累积分布函数	${\displaystyle {\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\!}$
期望	${\displaystyle \mu }$
中位数	${\displaystyle \mu }$
众数	${\displaystyle \mu }$
方差	${\displaystyle \sigma ^{2}}$
偏度	0
峰度	0
熵	${\displaystyle \ln \left(\sigma {\sqrt {2\,\pi \,e}}\right)\!}$
矩生成函数	${\displaystyle M_{X}(t)=\exp \left(\mu \,t+\sigma ^{2}{\frac {t^{2}}{2}}\right)}$
特征函数	${\displaystyle \phi _{X}(t)=\exp \left(\mu \,i\,t-{\frac {\sigma ^{2}t^{2}}{2}}\right)}$

“normal distribution”的各地常用译名
中国大陆	正态分布
台湾	常态分布
港澳	常态分布、正态分布
日本	正規分布
韩国	正規分布

若随机变量${\displaystyle X}$服从一个平均数为${\displaystyle \mu }$、标准差为${\displaystyle \sigma }$的正态分布，则记为：

${\displaystyle X\sim N(\mu ,\sigma ^{2}),}$^[4]

则其概率密度函数为 ${\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\;e^{-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}}\!}$^[4][5]

正态分布的数学期望值或期望${\displaystyle \mu }$,可解释为位置参数，决定了分布的位置；其方差${\displaystyle \sigma ^{2}}$的平方根或标准差${\displaystyle \sigma }$可解释尺度参数，决定了分布的幅度。^[5]

中心极限定理指出，在特定条件下，一个具有有限均值和方差的随机变量的多个样本(观察值)的平均值本身就是一个随机变量，其分布随着样本数量的增加而收敛于正态分布。因此，许多与独立过程总和有关的物理量，例如测量误差，通常可被近似为正态分布。

正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线（类似于寺庙里的大钟，因此得名）。我们通常所说的标准正态分布是位置参数${\displaystyle \mu =0}$，尺度参数${\displaystyle \sigma ^{2}=1}$的正态分布^[5]（见右图中红色曲线）。

概要

正态分布是自然科学与行为科学中的定量现象的一个方便模型。各种各样的心理学测试分数和物理现象比如光子计数都被发现近似地服从正态分布。尽管这些现象的根本原因经常是未知的，理论上可以证明如果把许多小作用加起来看做一个变量，那么这个变量服从正态分布（在R.N.Bracewell的Fourier transform and its application中可以找到一种简单的证明）。正态分布出现在许多区域统计：例如，采样分布均值是近似地正态的，即使被采样的样本的原始群体分布并不服从正态分布。另外，正态分布信息熵在所有的已知均值及方差的分布中最大，这使得它作为一种均值以及方差已知的分布的自然选择。正态分布是在统计以及许多统计测试中最广泛应用的一类分布。在概率论，正态分布是几种连续以及离散分布的极限分布。

历史

正态分布最早是棣莫弗在1718年著作的书籍的（Doctrine of Change），及1734年发表的一篇关于二项分布文章中提出的，当二项随机变量的位置参数n很大及形状参数p为1/2时，则所推导出二项分布的近似分布函数就是正态分布。拉普拉斯在1812年发表的《分析概率论》（Theorie Analytique des Probabilites）中对棣莫佛的结论作了扩展到二项分布的位置参数为n及形状参数为1>p>0时。现在这一结论通常被称为棣莫佛－拉普拉斯定理。

拉普拉斯在误差分析试验中使用了正态分布。勒让德于1805年引入最小二乘法这一重要方法；而高斯则宣称他早在1794年就使用了该方法，并通过假设误差服从正态分布给出了严格的证明。

将正态分布称作“钟形曲线”的习惯可以追溯到Jouffret他在1872年首次提出这个术语（Bell curve）用来指代二元正态分布。正态分布这个名字还被查尔斯·皮尔士、法兰西斯·高尔顿、威尔赫姆·莱克希斯在1875分别独立地使用。这个术语是不幸的，因为它反映和鼓励了一种谬误，即很多概率分布都是正态的。（请参考下面的“实例”）

这个分布被称为“正态”或者“高斯”正好是史蒂格勒名字由来法则的一个例子，这个法则说“没有科学发现是以它最初的发现者命名的”。

正态分布的定义

有几种不同的方法用来说明一个随机变量。最直观的方法是概率密度函数，这种方法能够表示随机变量每个取值有多大的可能性。累积分布函数是一种概率上更加清楚的方法，请看下边的例子。还有一些其他的等价方法，例如cumulant、特征函数、矩生成函数以及cumulant-生成函数。这些方法中有一些对于理论工作非常有用，但是不够直观。请参考关于概率分布的讨论。

概率密度函数

四个不同参数集的概率密度函数（红色线代表标准正态分布）

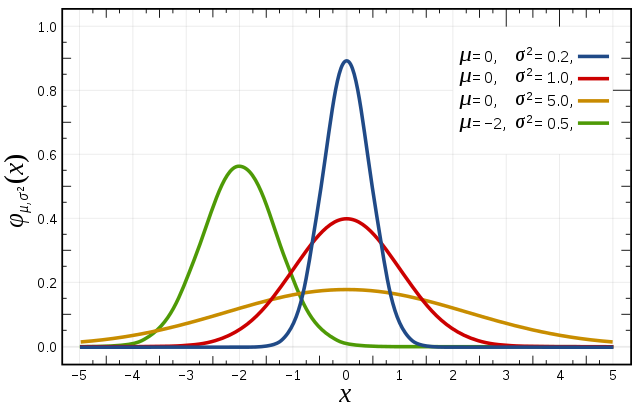
正态分布的概率密度函数均值为${\displaystyle \mu }$ 方差为${\displaystyle \sigma ^{2}}$ (或标准差${\displaystyle \sigma }$)是高斯函数的一个实例：

${\displaystyle f(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\,\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}$。

(请看指数函数以及${\displaystyle \pi }$.)

如果一个随机变量${\displaystyle X}$服从这个分布，我们写作 ${\displaystyle X}$ ~ ${\displaystyle N(\mu ,\sigma ^{2})}$. 如果${\displaystyle \mu =0}$并且${\displaystyle \sigma =1}$，这个分布被称为标准正态分布，这个分布能够简化为

${\displaystyle f(x)={\frac {1}{\sqrt {2\pi }}}\,\exp \left(-{\frac {x^{2}}{2}}\right)}$。

右边是给出了不同参数的正态分布的函数图。

正态分布中一些值得注意的量：

• 密度函数关于平均值对称
• 平均值与它的众数（statistical mode）以及中位数（median）同一数值。
• 函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。
• 95.449974%的面积在平均数左右两个标准差${\displaystyle 2\sigma }$的范围内。
• 99.730020%的面积在平均数左右三个标准差${\displaystyle 3\sigma }$的范围内。
• 99.993666%的面积在平均数左右四个标准差${\displaystyle 4\sigma }$的范围内。
• 函数曲线的拐点（inflection point）为离平均数一个标准差距离的位置。

累积分布函数

上图所示的概率密度函数的累积分布函数

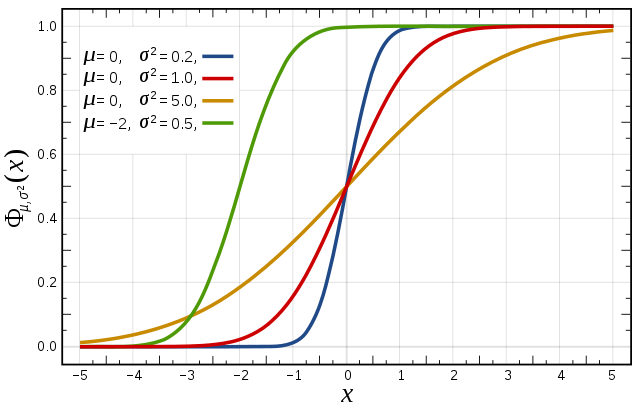
累积分布函数是指随机变量${\displaystyle X}$小于或等于${\displaystyle x}$的概率，用概率密度函数表示为

${\displaystyle F(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{x}\exp \left(-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}\ \right)\,dt.}$

正态分布的累积分布函数能够由一个叫做误差函数的特殊函数表示：

${\displaystyle \Phi (z)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {z-\mu }{\sigma {\sqrt {2}}}}\right)\right].}$

标准正态分布的累积分布函数习惯上记为${\displaystyle \Phi }$，它仅仅是指${\displaystyle \mu =0}$，${\displaystyle \sigma =1}$时的值，

${\displaystyle \Phi (x)=F(x;0,1)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}\exp \left(-{\frac {t^{2}}{2}}\right)\,dt.}$

将一般正态分布用误差函数表示的公式简化，可得：

${\displaystyle \Phi (z)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {z}{\sqrt {2}}}\right)\right].}$

它的反函数被称为反误差函数，为：

${\displaystyle \Phi ^{-1}(p)={\sqrt {2}}\;\operatorname {erf} ^{-1}\left(2p-1\right).}$

该分位数函数有时也被称为probit函数。probit函数已被证明没有初等原函数。

正态分布的分布函数${\displaystyle \Phi (x)}$没有解析表达式，它的值可以通过数值积分、泰勒级数或者渐进序列近似得到。

生成函数

矩母函数

矩生成函数，或称矩母函数被定义为${\displaystyle \exp(tX)}$的期望。

正态分布的矩产生函数如下：

${\displaystyle M_{X}(t)\,}$	${\displaystyle =\mathrm {E} \left(e^{tX}\right)}$
	${\displaystyle =\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}e^{tx}\,dx}$
	${\displaystyle =e^{\left(\mu t+{\frac {\sigma ^{2}t^{2}}{2}}\right)}}$

可以通过在指数函数内配平方得到。

特征函数

特征函数被定义为${\displaystyle \exp(itX)}$的期望，其中${\displaystyle i}$是虚数单位. 对于一个正态分布来讲，特征函数是：

${\displaystyle \phi _{X}(t;\mu ,\sigma )\!}$	${\displaystyle =\mathrm {E} \left[\exp(itX)\right]}$
	${\displaystyle =\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\exp(itx)\,dx}$
	${\displaystyle =\exp \left(i\mu t-{\frac {\sigma ^{2}t^{2}}{2}}\right).}$

把矩生成函数中的${\displaystyle t}$换成${\displaystyle it}$就能得到特征函数。

性质

正态分布的一些性质：

1. 如果${\displaystyle X\sim N(\mu ,\sigma ^{2})\,}$且${\displaystyle a}$与${\displaystyle b}$是实数，那么${\displaystyle aX+b\sim N(a\mu +b,(a\sigma )^{2})}$ (参见期望和方差).
2. 如果${\displaystyle X\sim N(\mu _{X},\sigma _{X}^{2})}$与${\displaystyle Y\sim N(\mu _{Y},\sigma _{Y}^{2})}$是统计独立的正态随机变量，那么：
   • 它们的和也满足正态分布${\displaystyle U=X+Y\sim N(\mu _{X}+\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$ (proof（英语：sum of normally distributed random variables）).
   • 它们的差也满足正态分布${\displaystyle V=X-Y\sim N(\mu _{X}-\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$.
   • ${\displaystyle U}$与${\displaystyle V}$两者是相互独立的。（要求X与Y的方差相等）
3. 如果${\displaystyle X\sim N(0,\sigma _{X}^{2})}$和${\displaystyle Y\sim N(0,\sigma _{Y}^{2})}$是独立正态随机变量，那么：
   • 它们的积${\displaystyle XY}$服从概率密度函数为${\displaystyle p}$的分布

     ${\displaystyle p(z)={\frac {1}{\pi \,\sigma _{X}\,\sigma _{Y}}}\;K_{0}\left({\frac {|z|}{\sigma _{X}\,\sigma _{Y}}}\right),}$其中${\displaystyle K_{0}}$是修正贝塞尔函数（modified Bessel function）

   • 它们的比符合柯西分布，满足${\displaystyle X/Y\sim \mathrm {Cauchy} (0,\sigma _{X}/\sigma _{Y})}$.
4. 如果${\displaystyle X_{1},\cdots ,X_{n}}$为独立标准正态随机变量，那么${\displaystyle X_{1}^{2}+\cdots +X_{n}^{2}}$服从自由度为n的卡方分布。

标准化正态随机变量

矩（moment）

一些正态分布的一阶矩如下：

阶数	原点矩	中心矩	累积量
0	1	0
1	${\displaystyle \mu }$	0	${\displaystyle \mu }$
2	${\displaystyle \mu ^{2}+\sigma ^{2}}$	${\displaystyle \sigma ^{2}}$	${\displaystyle \sigma ^{2}}$
3	${\displaystyle \mu ^{3}+3\mu \sigma ^{2}}$	0	0
4	${\displaystyle \mu ^{4}+6\mu ^{2}\sigma ^{2}+3\sigma ^{4}}$	${\displaystyle 3\sigma ^{4}}$	0

标准正态的所有二阶以上的累积量为零。

生成正态随机变量

中心极限定理

主条目：中心极限定理

正态分布的概率密度函数，参数为μ = 12，σ = 3，趋近于n = 48、p = 1/4的二项分布的概率质量函数。

正态分布有一个非常重要的性质：在特定条件下，大量统计独立的随机变量的平均值的分布趋于正态分布，这就是中心极限定理。中心极限定理的重要意义在于，根据这一定理的结论，其他概率分布可以用正态分布作为近似。

• 参数为${\displaystyle n}$和${\displaystyle p}$的二项分布，在${\displaystyle n}$相当大而且${\displaystyle p}$接近0.5时近似于正态分布（有的参考书建议仅在${\displaystyle np}$与${\displaystyle n(1-p)}$至少为5时才能使用这一近似）。

近似正态分布平均数为${\displaystyle \mu =np}$且方差为${\displaystyle \sigma ^{2}=np(1-p)}$.

• 一泊松分布带有参数${\displaystyle \lambda }$当取样样本数很大时将近似正态分布${\displaystyle \lambda }$.

近似正态分布平均数为${\displaystyle \mu =\lambda }$且方差为${\displaystyle \sigma ^{2}=\lambda }$.

这些近似值是否完全充分正确取决于使用者的使用需求

无限可分性

正态分布是无限可分的概率分布。

稳定性

正态分布是严格稳定的概率分布。

标准偏差

深蓝色区域是距平均值小于一个标准差之内的数值范围。在正态分布中，此范围所占比率为全部数值之68%，根据正态分布，两个标准差之内的比率合起来为95%；三个标准差之内的比率合起来为99%。

在实际应用上，常考虑一组数据具有近似于正态分布的概率分布。若其假设正确，则约68.3%数值分布在距离平均值有1个标准差之内的范围，约95.4%数值分布在距离平均值有2个标准差之内的范围，以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则”。

数字比率 标准差值	概率	包含之外比例
	百分比	百分比	比例
6999318639000000000♠0.318639σ	25%	75%	3 / 4
6999674490000000000♠0.674490σ	7001500000000000000♠50%	7001500000000000000♠50%	1 / 7000200000000000000♠2
6999994458000000000♠0.994458σ	68%	32%	1 / 3.125
1σ	7001682689492000000♠68.2689492%	7001317310508000000♠31.7310508%	1 / 7000315148720000000♠3.1514872
7000128155200000000♠1.281552σ	80%	20%	1 / 5
7000164485400000000♠1.644854σ	90%	10%	1 / 10
7000195996400000000♠1.959964σ	95%	5%	1 / 20
2σ	7001954499736000000♠95.4499736%	7000455002640000000♠4.5500264%	1 / 7001219778950000000♠21.977895
7000257582900000000♠2.575829σ	99%	1%	1 / 100
3σ	7001997300204000000♠99.7300204%	6999269979600000000♠0.2699796%	1 / 370.398
7000329052700000000♠3.290527σ	99.9%	0.1%	1 / 7003100000000000000♠1000
7000389059200000000♠3.890592σ	99.99%	0.01%	1 / 7004100000000000000♠10000
4σ	7001999936660000000♠99.993666%	6997633400000000000♠0.006334%	1 / 7004157870000000000♠15787
7000441717300000000♠4.417173σ	99.999%	0.001%	1 / 7005100000000000000♠100000
7000450000000000000♠4.5σ	99.9993204653751%	0.0006795346249%	1 / 7005147159535800000♠147159.5358 3.4 / 7006100000000000000♠1000000 (每一边)
7000489163800000000♠4.891638σ	7001999999000000000♠99.9999%	6996100000000000000♠0.0001%	1 / 7006100000000000000♠1000000
5σ	7001999999426697000♠99.9999426697%	6995573303000000000♠0.0000573303%	1 / 7006174427800000000♠1744278
7000532672399999999♠5.326724σ	7001999999900000000♠99.99999%	6995100000000000000♠0.00001%	1 / 7007100000000000000♠10000000
7000573072900000000♠5.730729σ	7001999999990000000♠99.999999%	6994100000000000000♠0.000001%	1 / 7008100000000000000♠100000000
7000600000000000000♠6σ	7001999999998027000♠99.9999998027%	6993197300000000000♠0.0000001973%	1 / 7008506797346000000♠506797346
7000610941000000000♠6.109410σ	7001999999999000000♠99.9999999%	6993100000000000000♠0.0000001%	1 / 7009100000000000000♠1000000000
7000646695100000000♠6.466951σ	7001999999999900000♠99.99999999%	6992100000000000000♠0.00000001%	1 / 7010100000000000000♠10000000000
7000680650200000000♠6.806502σ	7001999999999990000♠99.999999999%	6991100000000000000♠0.000000001%	1 / 7011100000000000000♠100000000000
7σ	99.9999999997440%	6990256000000000000♠0.000000000256%	1 / 7011390682215445000♠390682215445

相关分布

• ${\displaystyle R\sim \mathrm {Rayleigh} (\sigma )}$是瑞利分布，如果${\displaystyle R={\sqrt {X^{2}+Y^{2}}}}$，这里${\displaystyle X\sim N(0,\sigma ^{2})}$和${\displaystyle Y\sim N(0,\sigma ^{2})}$是两个独立正态分布。
• ${\displaystyle Y\sim \chi _{\nu }^{2}}$是卡方分布具有${\displaystyle \nu }$自由度，如果${\displaystyle Y=\sum _{k=1}^{\nu }X_{k}^{2}}$这里${\displaystyle X_{k}\sim N(0,1)}$其中${\displaystyle k=1,\dots ,\nu }$是独立的。
• ${\displaystyle Y\sim \mathrm {Cauchy} (\mu =0,\theta =1)}$是柯西分布，如果${\displaystyle Y=X_{1}/X_{2}}$，其中${\displaystyle X_{1}\sim N(0,1)}$并且${\displaystyle X_{2}\sim N(0,1)}$是两个独立的正态分布。
• ${\displaystyle Y\sim {\mbox{Log-N}}(\mu ,\sigma ^{2})}$是对数正态分布如果${\displaystyle Y=e^{X}}$并且${\displaystyle X\sim N(\mu ,\sigma ^{2})}$.
• 与Lévy skew alpha-stable分布相关：如果${\displaystyle X\sim {\textrm {Levy-S}}\alpha {\textrm {S}}(2,\beta ,\sigma /{\sqrt {2}},\mu )}$因而${\displaystyle X\sim N(\mu ,\sigma ^{2})}$.

估计

参数的最大似然估计

概念一般化

多元正态分布的协方差矩阵的估计的推导是比较难于理解的。它需要了解谱原理（spectral theorem）以及为什么把一个标量看做一个1×1矩阵的迹（trace）而不仅仅是一个标量更合理的原因。请参考协方差矩阵的估计（estimation of covariance matrices）。

参数的矩估计

常见实例

光子计数

计量误差

饮料装填量不足与超量的概率

某饮料公司装瓶流程严谨，每罐饮料装填量符合平均600毫升，标准差3毫升的正态分配法则。随机选取一罐，求（1）容量超过605毫升的概率；（2）容量小于590毫升的概率。

容量超过605毫升的概率 = p ( X > 605)= p ( ((X-μ) /σ) > ( (605 – 600) / 3) )= p ( Z > 5/3) = p( Z > 1.67) = 1 - 0.9525 = 0.0475

容量小于590毫升的概率 = p (X < 590) = p ( ((X-μ) /σ) < ( (590 – 600) / 3) )= p ( Z < -10/3) = p( Z < -3.33) = 0.0004

6-标准差(6-sigma或6-σ)的品质管制标准

6-标准差(6-sigma或6-σ)，是制造业流行的品质管制标准。在这个标准之下，一个标准正态分配的变数值出现在正负三个标准差之外，只有2* 0.0013= 0.0026 (p (Z < -3) = 0.0013以及p(Z > 3) = 0.0013)。也就是说，这种品质管制标准的产品不良率只有万分之二十六。假设例中的饮料公司装瓶流程采用这个标准，而每罐饮料装填量符合平均600毫升，标准差3毫升的正态分配。那么预期装填容量的范围应该多少？

6-标准差的范围 = p ( -3 < Z < 3)= p ( - 3 < (X-μ) /σ < 3) = p ( -3 < (X- 600) / 3 < 3)= p ( -9 < X – 600 < 9) = p (591 < X < 609) 因此，预期装填容量应该介于591至609毫升之间。

生物标本的物理特性

金融变量

寿命

测试和智力分布

计算学生智商高低的概率

假设某校入学新生的智力测验平均分数与标准差分别为100与12。那么随机抽取50个学生，他们智力测验平均分数大于105的概率？小于90的概率？

本例没有正态分配的假设，还好中心极限定理提供一个可行解，那就是当随机样本长度超过30，样本平均数${\displaystyle {\bar {x}}}$近似于一个正态变数，

因此标准正态变数${\displaystyle Z={\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}}$。

平均分数大于105的概率 ${\displaystyle P(Z>{\frac {105-100}{12/{\sqrt {50}}}})=P(Z>5/1.7)=P(Z>2.94)=0.0016}$

平均分数小于90的概率 ${\displaystyle P(Z<{\frac {90-100}{12/{\sqrt {50}}}})=P(Z<-5.88)=0.0000}$

计算统计应用

生成正态分布随机变量

在计算机模拟中，经常需要生成正态分布的数值。最基本的一个方法是使用标准的正态累积分布函数的反函数。除此之外还有其他更加高效的方法，Box-Muller变换就是其中之一。另一个更加快捷的方法是ziggurat算法。下面将介绍这两种方法。一个简单可行的并且容易编程的方法是：求12个在（0,1）上均匀分布的和，然后减6(12的一半)。这种方法可以用在很多应用中。这12个数的和是Irwin-Hall分布；选择一个方差12。这个随即推导的结果限制在（-6,6）之间，并且密度为12，是用11次多项式估计正态分布。

Box-Muller方法是以两组独立的随机数U和V，这两组数在(0,1]上均匀分布，用U和V生成两组独立的标准正态分布随机变量X和Y:

${\displaystyle X={\sqrt {-2\ln U}}\,\cos(2\pi V),}$

${\displaystyle Y={\sqrt {-2\ln U}}\,\sin(2\pi V)}$。

这个方程的提出是因为二自由度的卡方分布（见性质4）很容易由指数随机变量（方程中的lnU）生成。因而通过随机变量V可以选择一个均匀环绕圆圈的角度，用指数分布选择半径然后变换成（正态分布的）x,y坐标。

参考文献

1. 物理学名词审定委员会．物理学名词 [S/OL]．全国科学技术名词审定委员会,公布. 3版．北京：科学出版社, 2019: 12. 科学文库 （页面存档备份，存于互联网档案馆）.
2. Normal Distribution （页面存档备份，存于互联网档案馆）, Gale Encyclopedia of Psychology
3. Casella & Berger (2001，第102页) harvtxt模板错误: 无指向目标: CITEREFCasellaBerger2001 (帮助)
4. McPherson (1990，第110页) harvtxt模板错误: 无指向目标: CITEREFMcPherson1990 (帮助)
5. Shaou-Gang Miaou; Jin-Syan Chou. 《Fundamentals of probability and statistics》. 高立图书. 2012: 第147页. ISBN 9789864128990. 引文使用过时参数coauthors (帮助)

• John Aldrich. Earliest Uses of Symbols in Probability and Statistics.网上材料，2006年6月3日存在.(See "Symbols associated with the Normal Distribution".)
• Abraham de Moivre (1738年). The Doctrine of Chances.
• Stephen Jay Gould (1981年). The Mismeasure of Man. First edition. W. W. Norton. ISBN 978-0-393-01489-1.
• R. J. Herrnstein and Charles Murray (1994年). The Bell Curve: Intelligence and Class Structure in American Life. Free Press. ISBN 978-0-02-914673-6.
• Pierre-Simon Laplace (1812年). Analytical Theory of Probabilities.
• Jeff Miller, John Aldrich, et al. Earliest Known Uses of Some of the Words of Mathematics. In particular, the entries for "bell-shaped and bell curve", "normal" (distribution), "Gaussian", and "Error, law of error, theory of errors, etc.".网上材料，2006年6月3日存在
• S. M. Stigler (1999年). Statistics on the Table, chapter 22. Harvard University Press. (History of the term "normal distribution".)
• Eric W. Weisstein et al. Normal Distribution （页面存档备份，存于互联网档案馆） at MathWorld.网上材料，2006年6月3日存在。
• Marvin Zelen and Norman C. Severo (1964年). Probability Functions. Chapter 26 of Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, ed, by Milton Abramowitz and Irene A. Stegun. National Bureau of Standards.

外部链接

• Interactive Distribution Modeler (incl. Normal Distribution) （页面存档备份，存于互联网档案馆）.
• basic tools for sixsigma （页面存档备份，存于互联网档案馆）
• PlanetMath: normal random variable （页面存档备份，存于互联网档案馆）
• GNU Scientific Library – Reference Manual – The Gaussian Distribution （页面存档备份，存于互联网档案馆）
• Distribution Calculator （页面存档备份，存于互联网档案馆） – Calculates probabilities and critical values for normal, t, chi-square and F-distribution.
• Inverse Cumulative Standard Normal Distribution Function
• Is normal distribution due to Karl Gauss? Euler, his family of gamma functions, and place in history of statistics
• Maxwell demons: Simulating probability distributions with functions of propositional calculus
• Normal distribution table （页面存档备份，存于互联网档案馆）
• The Doctrine of Chance （页面存档备份，存于互联网档案馆） at MathPages.
• 正态分布的前世今生(上)
• 正态分布的前世今生(下)
• 在线计算器 正态分布 （页面存档备份，存于互联网档案馆）
• Binomial Distribution Calculator （页面存档备份，存于互联网档案馆）

参见

• 数学主题
• 统计学主题

• 中心极限定理
• 概率论
• 伽玛分布