三角化四面体

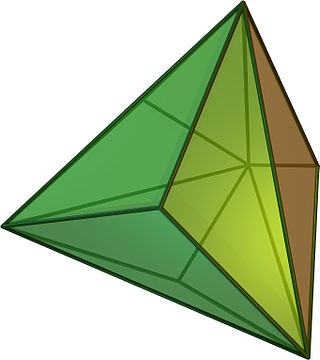
在几何学中，三角化四面体（英语：triakis tetrahedron或kistetrahedron^[2]）是一种卡塔兰多面体，其为截角正四面体的对偶多面体^[3]。

三角化四面体

（单击查看旋转模型）
类别	卡塔兰立体
对偶多面体	截角正四面体
识别
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	tikit
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）
性质
面	12
边	18
顶点	8
欧拉特征数	F=12, E=18, V=8 （χ=2）
二面角	129° 31' 16" ${\displaystyle \arccos(-{\frac {7}{11}})}$
组成与布局
面的种类	等腰三角形
面的布局 （英语：Face configuration）	V3.6.6
顶点图	4{3}+4{6}
对称性
对称群	Td, A3, [3,3], *332
旋转对称群 （英语：Rotation_groups）	T, [3,3]+, 332
特性
凸、face-transitive
图像
截角正四面体 （对偶多面体） （展开图）
查 论 编

在矿物学中，这种形状又称为三四面体^[4]（英语：tristetrahedron^[5][6]）。

性质

三角化四面体的旋转透视图。

三角化四面体是一种卡塔兰立体，由12个面、18条边和8个顶点组成^[7]，对偶多面体是一个阿基米德立体——截角四面体^[7][3]。由于其对偶多面体具有点可递的性质，因此三角化四面体拥有面可递的性质，即所有面皆全等。三角化四面体由12个全等的等腰三角形组成，其顶点有两种：一种为3个等腰三角形的公共顶点，另一种为6个等腰三角形的公共顶点。

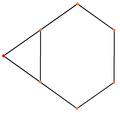
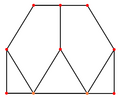
三角化四面体可以看做是在正四面体每个面上加上锥高为${\displaystyle {\frac {\sqrt {6}}{15}}}$倍边长的三角锥后所形成的形状^[8]，可以视为正三角形三边各加一个等腰三角形拼成的正六边形在立体几何中的推广。

面的组成

三角化四面体的面由12个全等的等腰三角形组成^[9]，三角形的边长比为3:3:5^[10][9]。

组成三角化四面体的等腰三角形，其顶角为${\displaystyle 2\cot ^{-1}{\frac {\sqrt {11}}{5}}}$约为112.89°、底角为${\displaystyle \tan ^{-1}{\frac {\sqrt {11}}{5}}}$约为33.56°。

体积与表面积

一个最短边长为单位长的三角化四面体，它的表面积为${\displaystyle {\tfrac {5}{3}}\scriptstyle {\sqrt {11}}}$，体积为${\displaystyle {\tfrac {25}{36}}\scriptstyle {\sqrt {2}}}$^[8]。

另一方面，也可以从其对偶多面体来计算体积。若其对偶多面体——截角四面体边长为a，可以先得出三角化四面体的边长：

短边为${\displaystyle {\frac {9}{5}}a=1.8a}$个单位长^[10][8]

长边为3a个单位长^[10][8]

半周长为${\displaystyle S={\frac {2\times {\frac {9}{5}}+3}{2}}a=3.3a}$，透过海伦公式可求得一个面的面积：

${\displaystyle {\sqrt {s(s-a)(s-b)(s-c)}}={\sqrt {3.3(3.3-{\frac {9}{5}})^{2}(3.3-3)}}a^{2}={\frac {9{\sqrt {11}}}{20}}a^{2}\approx 1.49248a^{2}}$^{[注 1]}

则体积V与表面积A为^[10]：

${\displaystyle V={\frac {81{\sqrt {2}}}{20}}a^{3}\approx 5.72756a^{3}}$

${\displaystyle A={\frac {27{\sqrt {11}}}{5}}a^{2}\approx 17.90977a^{2}}$

二面角

三角化四面体的二面角有2种结构，一种是等腰三角形长边与长边的二面角，另一种是短边与短边的二面角。两个二面角角度皆相同，其值为负十一分之七的反余弦值^[10]：

${\displaystyle \cos ^{-1}\left(-{\frac {7}{11}}\right)\approx 2.26057\approx 129.521196^{\circ }}$^[10]

正交投影

三角化四面体有4个特殊的正交投影，分别为于棱上投影（两种）、于面上投影和于面与顶点上投影。

正交投影

投影位置	于棱上投影	于面上投影	于面与顶点上投影	于棱上投影（交叉）
三角化 四面体
（对偶） 截角 四面体
投影 对称性	[1]	[1]	[3]	[4]

相关多面体与镶嵌

球面镶嵌版本的三角化四面体

三角化四面体是正四面体经过三角化变换后的结果，其他也是由正四面体透过康威变换得到的多面体有：

正四面体家族半正多面体

对称性: [3,3], (*332)							[3,3]+, (332)
{3,3}	t0,1{3,3}	t1{3,3}	t1,2{3,3}	t2{3,3}	t0,2{3,3}	t0,1,2{3,3}	s{3,3}
半正多面体对偶
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

三角化四面体是由等腰三角形组成，且对偶多面体由正六边形与正三角形交错组成。同样由等腰三角形组成，且对偶多面体由正多边形与正三角形交错组成的多面体或镶嵌图包括：

*n32变异对称性的截角镶嵌（英语：Template:Truncated figure1 table）: 3.2n.2n

对称性 *n32 [n,3]	球面镶嵌（英语：List_of_spherical_symmetry_groups）				欧氏镶嵌（英语：List_of_planar_symmetry_groups）	紧凑双曲		非紧双曲
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
截角镶嵌
顶点（英语：Vertex configuration）	3.4.4	3.6.6	3.8.8	3.10.10	3.12.12	3.14.14（英语：Truncated_heptagonal_tiling）	3.16.16（英语：Truncated octagonal tiling）	3.∞.∞（英语：Truncated order-3 apeirogonal tiling）
三角化 镶嵌
顶点（英语：Vertex configuration）	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14（英语：Truncated_heptagonal_tiling#Dual_tiling）	V3.16.16（英语：Truncated_octagonal_tiling#Dual_tiling）	V3.∞.∞（英语：Truncated_order-3_apeirogonal_tiling#Dual_tiling）

对偶复合体

复合截角四面体三角化四面体

复合截角四面体三角化四面体
类别	复合半正多面体
对偶多面体	自身对偶
性质
体	2
面	20
边	36
顶点	20
欧拉特征数	F=20, E=36, V=20 （χ=4）
组成与布局
复合几何体数量	2
复合几何体种类	1个三角化四面体 1个截角四面体
面的种类	12个等腰三角形 4个正三角形 4个正六边形
对称性
对称群	四面体群 (Td)
查 论 编

对偶复合体，即一个多面体与其对偶多面体组合成的复合图形。三角化四面体与其对偶的复合体为复合截角四面体三角化四面体。其共有20个面、36条边和20个顶点，其尤拉示性数为4，亏格为-1^[11]。

正交投影

以正六边形面为中心

以正三角形面为中心

面的组成

复合截角四面体三角化四面体由4个正三角形、4个正六边形和12个等腰三角形组成，其中组成的等腰三角形与三角化四面体完全相同，边长比同为3:3:5，但有部分隐没在截角四面体中，如下图所示，露在该立体外部的部分，以蓝色表示，隐没在立体内部的部分以白色表示，其中黑线代表等腰三角形与其对偶多面体截角四面体相交的位置：

复合截角四面体三角化四面体中的截角四面体亦有部分隐没在三角化四面体中，如下图所示：

正六边形面

正三角形面

对偶多面体

主条目：截角四面体

三角化四面体

对偶多面体： 截角四面体

三角化四面体的对偶多面体是一种由4个正三角形和4个正六边形组成的多面体^[12]，有12个顶点和18条棱，可以想象为将正四面体的顶点切去，称为截角四面体^[7][3][8]。

四半面体对称性

三角化四面体可以看做是四半面体^[13]对称性退化的极限：

四半面体变体的范例

其他变体

三角化四面体为正四面体每个面都加上适当高度的角锥所形成的几何形状^[9]。

而若加入的角锥为正三角锥（正四面体）则会产生正五胞体的展开图：

而若加入的角锥为直角三角锥，则会使等腰三角形两两共面形成立方体。可以透过在立方体的面上画上六个对角线看出此特性：

参见

• 截角三角化四面体

注解

1. 使用wolframalpha计算：[1] （页面存档备份，存于互联网档案馆）

参考文献

1. Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
2. Wenninger, Magnus（英语：Magnus J. Wenninger）, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371 (The thirteen semiregular convex polyhedra and their duals, Page 14, Triakistetrahedron)

1. The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [2] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Triakis tetrahedron)
2. Conway, Symmetries of things^[1], p.284
3. Holden, A. Shapes, Space, and Symmetry. New York: Columbia University Press, p. 55, 1971., p. 55
4. 三四面體 tristetrahedron. 国家教育研究院. [2018-08-23]. （原始内容存档于2018-08-26）.
5. Correns, C. W. Einführung in die Mineralogie (Kristallographie und Petrologie). Berlin: Springer-Verlag. 1949: p. 41. 引文格式1维护：冗余文本 (link)
6. Berry, L. G. and Mason, B. Mineralogy: Concepts, Descriptions, Determinations. San Francisco, CA: W. H. Freeman, 1959., p. 127
7. triakistetrahedron. bulatov.com. [2018-08-26]. （原始内容存档于2017-12-06）.
8. Weisstein, Eric W. (编). Triakis tetrahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
9. Triakis Tetrahedron Calculator. rechneronline.de. [2018-08-26]. （原始内容存档于2017-10-02）.
10. Catalan Solids: Triakis Tetrahedron. dmccooey.com. [2018-08-26]. （原始内容存档于2018-01-27）.
11. compound of truncated tetrahedron and triakistetrahedron. bulatov.org. [2018-08-26]. （原始内容存档于2017-12-06）.
12. Weisstein, Eric W. (编). Truncated tetrahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
13. 四半面體 tetartoid. 国家教育研究院. [2018-08-23]. （原始内容存档于2018-08-26）.

外部链接

• 埃里克·韦斯坦因, 三角化四面体 （参阅卡塔兰立体） 于MathWorld（英文）