包络

物理学和工程学中，震荡信号的包络是一条勾勒出极值的光滑曲线。^[1]因此，包络将恒定振幅的概念推广为瞬时振幅。下图展示了在上包络与下包络之间振荡的调制正弦曲线。包络函数可以是时间、空间、角度或任何变量的函数。

调制正弦曲线的包络

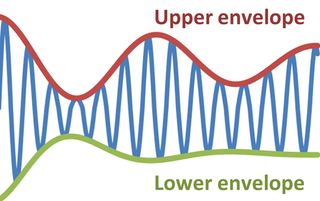
拍频波

由两个振幅相同、波长和频率几乎相同的正弦波相加产生的调制波。

在空间x和时间t中产生包络函数的常见情况是波长和频率几乎相同的两个波的叠加：^[2]

${\displaystyle {\begin{aligned}F(x,\ t)&=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]+\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]\\[6pt]&\approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\end{aligned}}}$

其中使用了两个正弦波相加的三角函数，以及近似值Δλ ≪ λ：

${\displaystyle {\frac {1}{\lambda \pm \Delta \lambda }}={\frac {1}{\lambda }}\ {\frac {1}{1\pm \Delta \lambda /\lambda }}\approx {\frac {1}{\lambda }}\mp {\frac {\Delta \lambda }{\lambda ^{2}}}.}$

此处调制波长λ_mod来自下式：^[2][3]

${\displaystyle \lambda _{\rm {mod}}={\frac {\lambda ^{2}}{\Delta \lambda }}\ .}$

调制波长是包络波长的两倍，因为余弦波的每半个波长都控制着正弦波的正负值。同样，拍频是包络波的频率，是调制波频率的两倍，即2Δf。^[4]

如果这种波是声波，耳朵听到的是与f有关的频率，振幅随拍频的变化而变化。^[4]

相速度与群速度

红色方块以相速度移动，绿色圆圈以群速度传播。

除2π之外，上述正弦波的参数是：

${\displaystyle \xi _{C}=\left({\frac {x}{\lambda }}-f\ t\right)\ ,}$

${\displaystyle \xi _{E}=\left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\ ,}$

下标C、E分别指载波和包络。同样的振幅F来自相同的ξ_C、ξ_E值，在适当相关的x、t选择下，每个本身都可能返回到相同的值。这种不变性意味着可以在空间中追踪波形，并找到固定振幅的位置在时间中传播时的速度；要使载波参数保持不变，条件为：

${\displaystyle \left({\frac {x}{\lambda }}-f\ t\right)=\left({\frac {x+\Delta x}{\lambda }}-f(t+\Delta t)\right)\ ,}$

这表明，要保持恒定振幅，距离Δx与时间间隔Δt的关系是相速度 v_p

${\displaystyle v_{\rm {p}}={\frac {\Delta x}{\Delta t}}=\lambda f\ .}$

另一方面，同样的考虑表明包络线是群速度 v_g:^[5]

${\displaystyle v_{\rm {g}}={\frac {\Delta x}{\Delta t}}=\lambda _{\rm {mod}}\Delta f=\lambda ^{2}{\frac {\Delta f}{\Delta \lambda }}\ .}$

引入波向量k，可得更常见的群速度表达式：

${\displaystyle k={\frac {2\pi }{\lambda }}\ .}$

注意到，对于微小变化Δλ而言，相应的波向量小变化Δk为：

${\displaystyle \Delta k=\left|{\frac {dk}{d\lambda }}\right|\Delta \lambda =2\pi {\frac {\Delta \lambda }{\lambda ^{2}}}\ ,}$

于是群速度可重写为：

${\displaystyle v_{\rm {g}}={\frac {2\pi \Delta f}{\Delta k}}={\frac {\Delta \omega }{\Delta k}}\ ,}$

其中ω是以弧度/秒为单位的频率：ω = 2πf。在所有介质中，频率和波向量都与色散关系ω = ω(k)有关，群速度可以写成：

${\displaystyle v_{\rm {g}}={\frac {d\omega (k)}{dk}}\ .}$

与GaAs晶格振动对应的某些波的色散关系ω=ω(k)。^[6]

在经典真空等介质中，电磁波的色散关系为：

${\displaystyle \omega =c_{0}k}$

其中c₀是经典真空中的光速。这种情况下，相速度和群速度都是c₀。

在所谓色散介质中，色散关系可能是波向量的复杂函数，相速度和群速度也不尽相同。例如，对于GaAs中原子振动（声子）表现出的几种波，不同波向量k方向的色散关系如图所示。一般而言，相速度和群速度的方向可能不同。^[7]

函数近似

参见：K·p微扰论

根据包络函数计算的GaAs-GaAlAs异质结中160Ǻ GaAs量子阱最低两个量子态的电子概率。^[8]

凝聚态物理学中，晶体中移动电荷载流子的能量本征函数可表为布洛赫波：

${\displaystyle \psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} )\ ,}$

其中n是带的编号（如导带或价带），r是空间位置，k是波矢。指数是正弦变化函数，对应一个缓慢变化的包络，调制波函数u_{n, k}的快速变化部分，描述波函数在晶格原子核心附近的行为。包络只限于晶体布里渊区限定范围内的k值，这就限制了它随位置r变化的速度。

用量子力学确定载流子行为时，通常使用包络近似法。其中薛定谔方程被简化到仅指包络的行为，边界条件直接应用于包络函数，而非完整的波函数。^[9]例如，被困在杂质附近的载流子波函数受包络函数F支配，函数是布洛赫函数的叠加：

${\displaystyle \psi (\mathbf {r} )=\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }u_{\mathbf {k} }(\mathbf {r} )\ ,}$

其中包括F(k)的傅立叶分量由近似薛定谔方程求得。^[10]在某些应用中，周期部分u_k被带缘附近的值取代，如k=k₀，接着：^[9]

${\displaystyle \psi (\mathbf {r} )\approx \left(\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }\right)u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )=F(\mathbf {r} )u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )\ .}$

衍射图样

双峰衍射图样具有单缝包络线。

多缝衍射图样的包络由单缝衍射图样决定，后者的包络线如下：^[11]

${\displaystyle I_{1}=I_{0}\sin ^{2}\left({\frac {\pi d\sin \alpha }{\lambda }}\right)/\left({\frac {\pi d\sin \alpha }{\lambda }}\right)^{2}\ ,}$

其中α是衍射角，d是狭缝宽度，λ是波长。对多个狭缝，图样为^[11]

${\displaystyle I_{q}=I_{1}\sin ^{2}\left({\frac {q\pi g\sin \alpha }{\lambda }}\right)/\sin ^{2}\left({\frac {\pi g\sin \alpha }{\lambda }}\right)\ ,}$

其中q为狭缝数量，g是光栅常数。第一个因子即单缝结果I₁，调制着第二个变化更快的因子，取决于狭缝数量与间距。

估计

包络检波器是从信号中提取包络的电子电路。

在数码信号处理中，可用希尔伯特变换或滑动平均RMS振幅估计包络。^[12]

另见

• 解析信号#复包络/基带

• 包络线
• 包络追踪
• 瞬时频率
• 调变
• 振动 (数学)

参考文献

1. C. Richard Johnson, Jr; William A. Sethares; Andrew G. Klein. Figure C.1: The envelope of a function outlines its extremes in a smooth manner. Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps. Cambridge University Press. 2011: 417. ISBN 978-0521189446.
2. Blair Kinsman. Wind Waves: Their Generation and Propagation on the Ocean Surface Reprint of Prentice-Hall 1965. Courier Dover Publications. 2002: 186. ISBN 0486495116.
3. Mark W. Denny. Air and Water: The Biology and Physics of Life's Media. Princeton University Press. 1993: 289. ISBN 0691025185. 含有内容需登入查看的页面 (link)
4. Paul Allen Tipler; Gene Mosca. Physics for Scientists and Engineers, Volume 1 6th. Macmillan. 2008: 538. ISBN 978-1429201247.
5. Peter W. Milonni; Joseph H. Eberly. §8.3 Group velocity. Laser Physics 2nd. John Wiley & Sons. 2010: 336. ISBN 978-0470387719.
6. Peter Y. Yu; Manuel Cardona. Fig. 3.2: Phonon dispersion curves in GaAs along high-symmetry axes. Fundamentals of Semiconductors: Physics and Materials Properties 4th. Springer. 2010: 111. ISBN 978-3642007095.
7. V. Cerveny; Vlastislav Červený. §2.2.9 Relation between the phase and group velocity vectors. Seismic Ray Theory. Cambridge University Press. 2005: 35. ISBN 0521018226.
8. G Bastard; JA Brum; R Ferreira. Figure 10 in Electronic States in Semiconductor Heterostructures. Henry Ehrenreich; David Turnbull (编). Solid state physics: Semiconductor Heterostructures and Nanostructures. 1991: 259. ISBN 0126077444.
9. Christian Schüller. §2.4.1 Envelope function approximation (EFA). Inelastic Light Scattering of Semiconductor Nanostructures: Fundamentals And Recent Advances. Springer. 2006: 22. ISBN 3540365257.
10. For example, see Marco Fanciulli. §1.1 Envelope function approximation. Electron Spin Resonance and Related Phenomena in Low-Dimensional Structures. Springer. 2009: 224 ff. ISBN 978-3540793649.
11. Kordt Griepenkerl. Intensity distribution for diffraction by a slit and Intensity pattern for diffraction by a grating. John W Harris; Walter Benenson; Horst Stöcker; Holger Lutz (编). Handbook of physics. Springer. 2002: 306 ff. ISBN 0387952691.
12. Envelope Extraction - MATLAB & Simulink. MathWorks. 2021-09-02 [2021-11-16]. （原始内容存档于2023-10-19）.