关系范畴

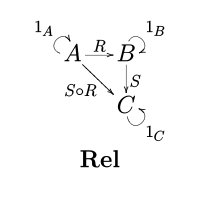
在数学上，关系范畴（记做Rel）指的是以集合为物件、以二元关系为态射的范畴。

关系范畴Rel.

Rel的反范畴Rel^op.

在这个范畴中，其态射${\displaystyle R:A\longrightarrow B}$是${\displaystyle A}$与${\displaystyle B}$之间的关系，因此${\displaystyle R\subseteq A\times B}$

这范畴中两个关系${\displaystyle R:A\longrightarrow B}$及${\displaystyle S:C\longrightarrow D}$的合成由下式给出：

${\displaystyle (a,c)\in S\circ R}$，当且仅当对于一些${\displaystyle b\in B}$而言，${\displaystyle (a,b)\in R}$且${\displaystyle (b,c)\in S}$^[1]

关系范畴又被一些人称为“集合间对应的范畴”（category of correspondences of sets）。^[2]

2 sources

性质

集合范畴是关系范畴的（宽）子范畴，其中集合范畴的态射${\displaystyle f:X\longrightarrow Y}$对应至以${\displaystyle (x,y)\in F\iff f(x)=y}$定义的关系${\displaystyle F\subseteq X\times Y}$。^[3][4]

关系范畴中的态射为关系，而其相对应的、从其反范畴（英语：opposite category）映至关系范畴的态射有着反向的箭头，因此这态射是个逆关系（英语：Converse relation），因此关系范畴包含其反范畴且是个自双对（英语：Dual (category theory)）。^[5]

由逆关系作代表所建构的对合为关系范畴提供了一个短剑结构，因此关系范畴是一个短剑范畴（英语：dagger category）。

关系范畴有两个做为同态函子（英语：hom functor）并映至自己的函子，其中一个是二元关系${\displaystyle R\subseteq A\times B}$，另一个则是其转置${\displaystyle R^{T}\subseteq B\times A}$，而这两个二元关系的两种合成关系分别为${\displaystyle RR^{T}}$及${\displaystyle R^{T}R}$，其中第一个合成关系${\displaystyle RR^{T}}$给出了A上的齐次关系（英语：homogeneous relation）；而第二个合成关系${\displaystyle R^{T}R}$则给出B上的齐次关系。由于这些函子是映至关系范畴自身的同态函子之故，因此这些同态函子是内部同态函子；而由于这些内部同态函子之故，因此关系范畴是个闭范畴（英语：Closed category），且是个短剑紧致范畴（英语：dagger compact category）。

关系范畴可以克莱斯利范畴（英语：Kleisli category）的形式，由集合范畴得到，在这种状况下，其有着以对应至幂集的函子为协变函子的单子。

一个第一眼看上去可能令人有点惊讶的事实是，关系范畴当中的乘法是以不相交联集（而非如集合范畴一般的笛卡尔积）定义的^[5]:181，而其余积（英语：Coproduct）亦然。

就其幺半乘积${\displaystyle A\otimes B}$与内部同态函子${\displaystyle A\implies B}$而言，关系范畴是个闭幺半范畴（英语：Closed monoidal category）。

关系范畴是Peter J. Freyd与Andre Scedrov在1990年给出的代数结构寓范畴（英语：Allegory (mathematics)）的原型^[6]，他们自正则范畴（英语：regular category）与${\displaystyle F:A\longrightarrow B}$出发，他们注意到了派生函子${\displaystyle Rel(A,B)\longrightarrow Rel(FA,FB)}$的性质，像例如说这函子保存了合成、逆转跟相交等运算，而他们之后以这样的性质建构了寓范畴的公理。

4 sources

关系作为物件

David Rydeheard与Rod Burstall认为关系范畴有著作为齐次关系物件，一个例子是${\displaystyle A}$是一个集合而${\displaystyle R\subseteq A\times A}$是一个二元关系；而这个范畴的态射是集合间保持关系的函数，在${\displaystyle S\subseteq B\times B}$是第二个关系且${\displaystyle f:A\longrightarrow B}$是一个使得${\displaystyle xRy\implies f(x)Sf(y),}$成立的函数，那${\displaystyle f}$是一个态射。^[7]

Adamek、Herrlich与Strecker三氏进一步发展了这想法，他们将物件${\displaystyle (A,R)}$与${\displaystyle (B,S)}$给设成（集合，关系）。^[8]

2 sources

参考资料

1. Mac Lane, S. Categories for the Working Mathematician 1st. New York: Springer-Verlag. 1988: 26. ISBN 0-387-90035-7.
2. Pareigis, Bodo. Categories and Functors. Pure and Applied Mathematics 39. Academic Press. 1970: 6. ISBN 978-0-12-545150-5.
3. Rydeheard与Burstall二氏将此范畴给记做Set_Rel
4. George Bergman (1998), An Invitation to General Algebra and Universal Constructions （页面存档备份，存于互联网档案馆）, §7.2 RelSet, Henry Helson Publisher, Berkeley. ISBN 0-9655211-4-1.
5. Michael Barr & Charles Wells (1998) Category Theory for Computing Science 互联网档案馆的存档，存档日期2016-03-04., page 83, from McGill University
6. Peter J. Freyd（英语：Peter J. Freyd） & Andre Scedrov (1990) Categories, Allegories, pages 79, 196, North Holland ISBN 0-444-70368-3
7. David Rydeheard & Rod Burstall（英语：Rod Burstall） (1988) Computational Category Theory, page 41, Prentice-Hall ISBN 978-0131627369
8. Juri Adamek, Horst Herrlich, and George E. Strecker (2004) [1990] Abstract and Concrete Categories （页面存档备份，存于互联网档案馆）, section 3.3, example 2(d) page 22, from Research group KatMAT （页面存档备份，存于互联网档案馆） at University of Bremen

• Francis Borceux. Handbook of Categorical Algebra: Volume 2, Categories and Structures. Cambridge University Press. 1994: 115 [2022-07-14]. ISBN 978-0-521-44179-7. （原始内容存档于2022-07-14）.