Loading AI tools
全等三角形指兩個全等的三角形,它們的三條邊及三個角都應對等。全等三角形是幾何中全等之一。根據全等轉換,兩個全等三角形可以平移、旋轉、軸對稱,或重疊等。
此條目需要補充更多來源。 (2024年10月19日) |
全等的數學符號為:
當使用該符號時,需保證符號兩邊的角、邊一一對應。
當有兩個或以上的三角形的對應邊及角,完全相等,便是全等三角形。

全等三角形有以下性質:
下列三對邊長為「對應邊」:
下列三對角為「對應角」:
同時,所有對應邊長及角度均相等:

下列五種方法均可驗證全等三角形:
- SSS(Side-Side-Side,邊、邊、邊;三邊):三邊長度相等。
- SAS(Side-Angle-Side,邊、角、邊;兩邊一夾角):兩邊,且夾角相等。
- ASA(Angle-Side-Angle,角、邊、角;兩角一夾邊):兩角,且夾邊相等。
- AAS(Angle-Angle-Side,角、角、邊;兩角一對邊):兩角,且非夾邊相等。
- RHS(Right angle-Hypotenuse-Side,直角、斜邊、邊,又稱 HL(斜邊、直角邊);斜股性質):在一對直角三角形中,斜邊及另一條直角邊相等。
下列兩種方法不能驗證為全等三角形:
- AAA(Angle-Angle-Angle,角、角、角):三角相等。不過它是證明相似三角形的一個條件。
- SSA(Side-Side-Angle,邊、邊、角):兩邊相等,而另一角(非夾角)相等。(但當該角是直角或鈍角時可確定三角形,而 RHS 便是該角是直角時的情形)
以上的各方法也可通過三角函數的相關定理證明。這相當於解三角形,即三條邊三個角一共六個量、固定其中三個而判斷剩下三個量是否有唯一解。
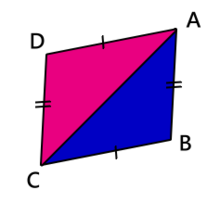
如右圖
| 原因 | |||
|---|---|---|---|
| 邊(一) | 公共邊 | ||
| 邊(二) | 已知 | ||
| 邊(三) | 已知 |
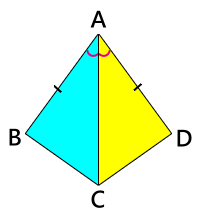
如右圖
| 原因 | |||
|---|---|---|---|
| 邊(一) | 公共邊 | ||
| 角 | 已知 | ||
| 邊(二) | 已知 |
此時兩邊夾一角已知,首先用餘弦定理計算第三邊,接下來與 SSS 的情況相同。
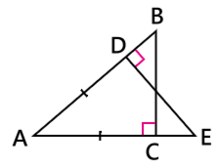
如右圖
| 原因 | |||
|---|---|---|---|
| 角(一) | 公共角 | ||
| 邊 | 已知 | ||
| 角(二) | 已知 |
此時兩角夾一邊已知,通過三角形內角和得到第三角後用正弦定理計算剩下兩邊。

RHS 判定定理在直角三角形中專用,也稱「HL」。即為直角三角形中的 SSA,也稱為斜股性質。如右圖
| 原因 | |||
|---|---|---|---|
| 直角 | 已知 | ||
| 斜邊 | 已知 | ||
| 邊 | 已知 |
勾股定理,或是直接連兩邊的頂端解出剩下一邊,即變成 SSS 或 SAS。

AAA(角、角、角),指兩個三角形的任何三個角都對應地相同。但這不能判定全等三角形,但AAA能判定相似三角形。在幾何學上,當兩條線疊在一起時,便會形一個點和一個角。而且,若該線無限地廷長,或無限地放大,該角度都不會改變。同理,在左圖中,該兩個三角形是相似三角形,這兩個三角形的關係是放大縮小,因此角度不會改變。
這樣,便能得知若邊無限地根據比例加長,角度都保持不變。因此,AAA 並不能判定全等三角形。
從正弦定理的角度看,
這個比例的比值可以任意縮放,因此無法唯一確定三邊長度。

SSA(邊、邊、角),也稱為 ASS ,指兩個三角形的任一角及另外兩個沒有夾着該角的邊相等。但這不能判定全等三角形。
在右圖中,分別有三角形 ABC 及三角形 DEF ,並提供了以下信息:
這即是 SSA。假如在右圖繪畫一個圓形,中心點為點E,半徑為。通過這個圓形便會發現:在和沒有改變的情況下,會出現另一個與一樣長度的直線(即圖中的)。這樣便能證明 SSA 並不能驗證全等三角形,(除非已知。當是直角三角形時應稱為RHS)。
雖然如此,當 ≥ 90°時,。又⇔,,故可驗證全等三角形。
再次使用正弦定理,
其中已知 、 和 ,可解出 ,但 在 0°到 180°上先升後降導致 有兩解,即 可能是鈍角或銳角(或退化為只有一解是直角的特殊情況,此處略去),分別對應圖中的 和 ,然而若已知該三角形是直角或鈍角三角形時,可以視情況排除掉其中的一個解、進而唯一確定 ,此時做減法得出 後即可用餘弦定理解得最後一邊 。
2016年,循道中學的校園電台在學校錄製了一首名叫《RHS》的歌曲,由校內三名學生主唱。創作概念是來自該學校的數學老師想令學生記得全等三角形的驗證方法。歌詞由上述老師於2014年創作,歌曲改編自1970年代德國流行樂隊 Silver Convention 歌曲《Fly, Robin, Fly》。
2016年4月18日,5分鐘的短片上傳到學校非官方Facebook專頁《MCKLN Secrets》後,因為歌詞重覆全等三角形的其中四個驗證方法,以及重覆有關的舞蹈動作[1]而瞬間爆紅。其歌詞為:
| “ | Side angle side, side side side, angle side angle, angle angle side! | ” |
影片首日上載吸引超過80萬次點擊觀看,而且被刊登於不同報刊,更被譽為「洗腦數學神曲」[2],以致被網民惡搞。關注社會基建工程等的本土研究社亦為此曲再填詞,製作了《嘥嘥嘥》短片,批評政府浪費公帑[3]。
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.











 ,
,  ...
...








 ...
...



 ...
...



 ,
,  ...
...























