餘弦定理

餘弦定理是三角形中三邊長度與一個角的餘弦值（${\displaystyle \cos }$）的數學式，餘弦定理指的是：

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma }$

一個三角形

同樣，也可以將其改為：

${\displaystyle b^{2}=c^{2}+a^{2}-2ca\cos \beta }$

${\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha }$

其中${\displaystyle c}$是${\displaystyle \gamma }$角的對邊，而${\displaystyle a}$和${\displaystyle b}$是${\displaystyle \gamma }$角的鄰邊。

勾股定理則是餘弦定理的特殊情況，當${\displaystyle \gamma }$為${\displaystyle 90^{\circ }}$時，${\displaystyle \cos \gamma =0}$，等式可被簡化為

${\displaystyle c^{2}=a^{2}+b^{2}}$

當知道三角形的兩邊和一角時，餘弦定理可被用來計算第三邊的長，或是當知道三邊的長度時，可用來求出任何一個角。

歷史

一個鈍三角形和它的高。

餘弦定理的歷史可追溯至公元三世紀前歐幾里得的幾何原本，在書中將三角形分為鈍角和銳角來解釋，這同時對應現代數學中餘弦值的正負。根據幾何原本第二卷的命題12和13^[1]，並參考右圖，以現代的數學式表示即為：

${\displaystyle {\overline {AB}}^{2}={\overline {CA}}^{2}+{\overline {CB}}^{2}+2({\overline {CA}})({\overline {CH}})\,}$

其中${\displaystyle {\overline {CH}}={\overline {BC}}\cos(\pi -\gamma )=-{\overline {BC}}\cos \gamma }$，將其帶入上式得到：

${\displaystyle {\overline {AB}}^{2}={\overline {CA}}^{2}+{\overline {CB}}^{2}-2({\overline {CA}})({\overline {BC}})\cos \gamma }$

證明

三角函數

具有垂直線的銳角三角形

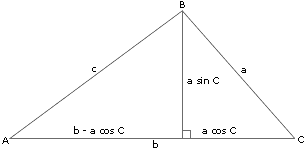
見右圖，在${\displaystyle c}$上做高可以得到（投影定理）：

${\displaystyle c=a\cos \beta +b\cos \alpha }$

將等式同乘以c得到：

${\displaystyle c^{2}=ac\cos \beta +bc\cos \alpha }$

運用同樣的方式可以得到：

${\displaystyle a^{2}=ac\cos \beta +ab\cos \gamma }$

${\displaystyle b^{2}=bc\cos \alpha +ab\cos \gamma }$

將${\displaystyle c^{2}}$的右式取代：

${\displaystyle c^{2}=ac\cos \beta +bc\cos \alpha =(a^{2}-ab\cos \gamma )+(b^{2}-ab\cos \gamma )=a^{2}+b^{2}-2ab\cos \gamma }$

勾股定理

勾股定理之一

設${\displaystyle \triangle ABC}$中，${\displaystyle {\overline {AB}}=c}$，${\displaystyle {\overline {BC}}=a}$，${\displaystyle {\overline {AC}}=b}$。過${\displaystyle B}$點作${\displaystyle AC}$的垂線，垂足為${\displaystyle D}$，如果${\displaystyle D}$在${\displaystyle AC}$內部，則${\displaystyle BD}$的長度為${\displaystyle a\sin C}$，${\displaystyle DC}$的長度為${\displaystyle a\cos C}$，${\displaystyle AD}$的長度為${\displaystyle b-a\cos C}$。根據勾股定理：

${\displaystyle c^{2}=(a\sin C)^{2}+(b-a\cos C)^{2}\,}$

${\displaystyle c^{2}=a^{2}\sin ^{2}C+b^{2}-2ab\cos C+a^{2}\cos ^{2}C\,}$

${\displaystyle c^{2}=a^{2}(\sin ^{2}C+\cos ^{2}C)+b^{2}-2ab\cos C\,}$

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C\,}$

如果${\displaystyle D}$在${\displaystyle AC}$的延長線上，證明是類似的。同理可以得到其他的等式。

勾股定理之二

證明所用的三角形

設${\displaystyle \triangle ABC}$中，${\displaystyle {\overline {AB}}=c}$，${\displaystyle {\overline {BC}}=a}$，${\displaystyle {\overline {AC}}=b}$。過${\displaystyle B}$點作${\displaystyle {\overline {AC}}}$的垂線，垂足為${\displaystyle D}$，設${\displaystyle {\overline {AD}}=x}$，則${\displaystyle {\overline {CD}}=b-x}$，根據勾股定理：

${\displaystyle c^{2}-x^{2}={\overline {BD}}^{2}=a^{2}-(b-x)^{2}}$

${\displaystyle c^{2}-x^{2}=a^{2}-b^{2}-x^{2}+2bx}$

${\displaystyle c^{2}=a^{2}-b^{2}+2bx}$

${\displaystyle x={\frac {b^{2}+c^{2}-a^{2}}{2b}}}$

${\displaystyle \cos A={\frac {x}{c}}={\frac {b^{2}+c^{2}-a^{2}}{2bc}}}$

如果${\displaystyle D}$在${\displaystyle {\overline {AC}}}$的延長線上，證明是類似的。同理可以得到其他的等式。

應用

餘弦定理是解三角形中的一個重要定理。

求邊

餘弦定理可以簡單地變形成：

${\displaystyle a={\sqrt {b^{2}+c^{2}-2bc\cos A}}}$

${\displaystyle b={\sqrt {c^{2}+a^{2}-2ac\cos B}}}$

${\displaystyle c={\sqrt {a^{2}+b^{2}-2ab\cos C}}}$

因此，如果知道了三角形的兩邊及其夾角，可由餘弦定理得出已知角的對邊。

求角

餘弦定理可以簡單地變形成：

${\displaystyle \cos A={\frac {b^{2}+c^{2}-a^{2}}{2bc}}\,\!}$

${\displaystyle \cos B={\frac {c^{2}+a^{2}-b^{2}}{2ca}}\,\!}$

${\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}\,\!}$

因為餘弦函數在${\displaystyle ({{\rm {0}},\pi })}$上的單調性，可以得到：

${\displaystyle \angle A=\arccos {\frac {b^{2}+c^{2}-a^{2}}{2bc}}\,\!}$

${\displaystyle \angle B=\arccos {\frac {c^{2}+a^{2}-b^{2}}{2ca}}\,\!}$

${\displaystyle \angle C=\arccos {\frac {a^{2}+b^{2}-c^{2}}{2ab}}\,\!}$

因此，如果已知三角形的三邊，可以由餘弦定理得到三角形的三個內角。

參見

• 三角形
• 勾股定理
• 正弦定理
• 正切定理
• 角平分線長公式
• 中線長公式

參考資料

• 數學主題

1. In obtuse-angled triangles the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle by twice the rectangle contained by one of the sides about the obtuse angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle. --- Euclid's Elements, translation by Thomas L. Heath.