在靜電學 裏，電勢 （electric potential/ ePtntl）又稱電位 （eForce/ eFrc)[ 1] 純量 ，操作型定義為「電場中某處的電勢」等於「處於電場 中該位置的單位電荷 所具有的電勢能 」[ 2] 伏特 。
本條目中，向量 與純量 分別用粗體 與斜體 顯示。例如，位置向量通常用
r
{\displaystyle \mathbf {r} \,\!}
r
{\displaystyle r\,\!}
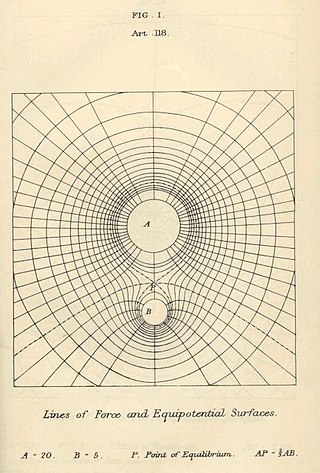
兩個同性電荷的電場線和等勢線。 電勢的數值不具有絕對意義，只具有相對意義，因此為了便於分析問題，必須設定一個參考位置，並把它設為零，稱為零位能點。通常，會把無窮遠處的電勢設定為零。那麼，電勢可以定義如下：假設檢驗電荷從無窮遠位置，經過任意路徑，克服電場力，以緩慢、沒有產生加速度的方式移動到某位置，則在這位置的電勢，等於因移動檢驗電荷所做的功 與檢驗電荷的電荷量 的比值。在國際單位制 裏，電勢的單位為伏特 （
V
=
J
/
C
{\displaystyle \scriptstyle {{\text{V}}={\text{J}}/{\text{C}}}}
亞歷山德羅·伏特 （Alessandro Volta）而命名。
電勢必需滿足帕松方程式 ，同時符合相關邊界條件；假設在某區域內的電荷密度 為零，則帕松方程式約化為拉普拉斯方程式 ，電勢必需滿足拉普拉斯方程式。
在電動力學 裏，當含時電磁場 存在的時候，電勢可以延伸為「廣義電勢」。特別注意，廣義電勢不能被視為電勢能每單位電荷。
處於外電場 的帶電粒子 會受到外電場施加的作用力 ，稱為電場力 ，促使帶電粒子加速運動。對於帶正電粒子，電場力與電場 同方向；對於帶負電粒子，電場力與電場反方向。電場力的數值大小與電荷量、電場數值大小成正比。
作用力 與位能 之間有非常直接的關係。隨着物體朝著作用力的方向的加速運動，物體的動能 變大，位能變小。例如，一個石頭在山頂的重力位能 大於在山腳的重力位能。隨着物體的滾落，重力位能變小，動能變大。
對於某種特別作用力，科學家可以定義其向量場 和其位勢 ，使得物體因為這向量場而具有的位能，只與物體位置、參考位置之間的距離有關。稱這種作用力為保守力 ，這種向量場為保守場 。
例如，重力 、靜電場的電場力，都是保守力。靜電場的純量勢 稱為電勢 ，或稱為靜電勢 。
電勢和磁向量勢 共同形成一個四維向量 ，稱為四維勢 。從某一個慣性參考系 觀察到的四維勢，應用勞侖茲變換 ，可以計算出另外一個慣性參考系所觀察到的四維勢。
由點電荷 Q 所產生的電勢，在距離 r 時，可表示為
V
=
1
4
π
ε
0
Q
r
{\displaystyle V={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}}}
其中，ε 0 是真空電容率 。
在無限遠處，電勢為零。由多個點電荷產生的電勢，相等於各點電荷所產生的電勢之和。此外，電勢場是純量場 ，電場則是向量場 。
電場遵守疊加原理 ：假設在三維空間裏，由兩組完全不相交的電荷分佈所產生的電場分別為
E
1
{\displaystyle \mathbf {E} _{1}}
E
2
{\displaystyle \mathbf {E} _{2}}
E
t
=
E
1
+
E
2
{\displaystyle \mathbf {E} _{t}=\mathbf {E} _{1}+\mathbf {E} _{2}}
總電勢為每單位電荷 克服電場力所做的機械功之和：
ϕ
t
(
r
)
=
−
∫
∞
r
E
t
⋅
d
ℓ
=
−
∫
∞
r
(
E
1
+
E
2
)
⋅
d
ℓ
=
ϕ
1
(
r
)
+
ϕ
2
(
r
)
{\displaystyle \phi _{t}(\mathbf {r} )=-\int _{\infty }^{\mathbf {r} }\mathbf {E} _{t}\cdot \mathrm {d} {\boldsymbol {\ell }}=-\int _{\infty }^{\mathbf {r} }(\mathbf {E} _{1}+\mathbf {E} _{2})\cdot \mathrm {d} {\boldsymbol {\ell }}=\phi _{1}(\mathbf {r} )+\phi _{2}(\mathbf {r} )}
所以，電勢也遵守疊加原理。當計算一組電荷分佈所產生的電勢時，只需要知道在電荷分佈的每個源位置的單獨電荷所產生在檢驗位置的電勢，就可以應用積分運算，得到整個電荷分佈所產生在檢驗位置的電勢。
應用積分符號內取微分 方法，電勢的梯度 為
∇
ϕ
(
r
)
=
−
∇
∫
∞
r
E
(
r
′
)
⋅
d
ℓ
′
=
−
E
(
r
)
{\displaystyle \mathbf {\nabla } \phi (\mathbf {r} )=-\mathbf {\nabla } \int _{\infty }^{\mathbf {r} }\mathbf {E} (\mathbf {r} ')\cdot \mathrm {d} {\boldsymbol {\ell }}^{\,\prime }=-\mathbf {E} (\mathbf {r} )}
所以，電場與電勢之間的關係為
E
(
r
)
=
−
∇
ϕ
(
r
)
{\displaystyle \mathbf {E} (\mathbf {r} )=-\mathbf {\nabla } \phi (\mathbf {r} )}
根據高斯定律 的方程式，
∇
⋅
E
=
ρ
/
ϵ
0
{\displaystyle \mathbf {\nabla } \cdot \mathbf {E} =\rho /\epsilon _{0}}
其中，
ρ
{\displaystyle \rho }
電荷密度 ，
ϵ
0
{\displaystyle \epsilon _{0}}
電常數 。
所以，電勢滿足帕松方程式 ：
∇
2
ϕ
=
−
ρ
/
ϵ
0
{\displaystyle \nabla ^{2}\phi =-\rho /\epsilon _{0}}
假設電荷密度為零，則這方程式變為拉普拉斯方程式 ：
∇
2
ϕ
=
0
{\displaystyle \nabla ^{2}\phi =0}
請注意，假若
∇
×
E
≠
0
{\displaystyle \mathbf {\nabla } \times \mathbf {E} \neq 0}
保守性 （由於隨時間變化的磁場 造成的效應；參閱麥克斯韋方程組 ），則不能使用這些方程式。
由於電勢乃是純量，而電場是具有三個分量的向量，所以，很多時候，使用電勢來解析問題會省去很多運算工作，帶來很大的便利。
在某空間區域內，假設電荷密度 為零，則電勢必須滿足拉普拉斯方程式 ，並且符合所有相關邊界條件 。
在靜電學裏，有三種邊界條件：
狄利克雷邊界條件 ：在所有邊界，電勢都已良態給定。具有這種邊界條件的問題稱為狄利克雷問題 。紐曼邊界條件 ：在所有邊界，電勢的法向導數都已良態給定。具有這種邊界條件的問題稱為紐曼問題 。混合邊界條件：一部分邊界的電勢都已良態給定，其它邊界的電勢的法向導數也已良態給定。 根據拉普拉斯方程式的唯一定理
應用分離變數法 來解析拉普拉斯方程式，可以將問題的偏微分方程式改變為一組較容易解析的常微分方程式 。對於一般問題，通常會採用直角坐標系、圓柱坐標系或球坐標系來分離拉普拉斯方程式。但是，對於其它比較特別的問題，另外還有八種坐標系可以用來分離拉普拉斯方程式。[ 3]
被位於
y
=
0
{\displaystyle y=0}
+ 、y- -半平面的兩個導體的電勢分別設定為
+
V
{\displaystyle +V}
−
V
{\displaystyle -V}
假設在xy-平面的無限平面導體 被一條位於
y
=
0
{\displaystyle y=0}
+ 、y- -半平面的導體的電勢分別設定為
+
V
{\displaystyle +V}
−
V
{\displaystyle -V}
+ -半空間任意位置的電勢這問題，由於邊界條件的幾何形狀適合用直角坐標來描述，可以以直角坐標
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
∇
2
ϕ
=
∂
2
ϕ
∂
x
2
+
∂
2
ϕ
∂
y
2
+
∂
2
ϕ
∂
z
2
=
0
{\displaystyle \nabla ^{2}\phi ={\frac {\partial ^{2}\phi }{\partial x^{2}}}+{\frac {\partial ^{2}\phi }{\partial y^{2}}}+{\frac {\partial ^{2}\phi }{\partial z^{2}}}=0}
因為這案例與x-坐標無關，方程式可以簡化為
∇
2
ϕ
(
y
,
z
)
=
∂
2
ϕ
∂
y
2
+
∂
2
ϕ
∂
z
2
=
0
{\displaystyle \nabla ^{2}\phi (y,z)={\frac {\partial ^{2}\phi }{\partial y^{2}}}+{\frac {\partial ^{2}\phi }{\partial z^{2}}}=0}
應用分離變數法，猜想解答的形式為
ϕ
(
y
,
z
)
=
Y
(
y
)
Z
(
z
)
{\displaystyle \phi (y,z)=Y(y)Z(z)}
將這公式代入拉普拉斯方程式，則可得到
1
Y
(
y
)
d
2
Y
(
y
)
d
y
2
+
1
Z
(
z
)
d
2
Z
(
z
)
d
z
2
=
0
{\displaystyle {\frac {1}{Y(y)}}\ {\frac {\mathrm {d} ^{2}Y(y)}{\mathrm {d} y^{2}}}+{\frac {1}{Z(z)}}\ {\frac {\mathrm {d} ^{2}Z(z)}{\mathrm {d} z^{2}}}=0}
注意到這方程式的每一個項目都只含有一個變量，並且跟其它變量無關。所以，每一個項目都等於常數：
1
Y
(
y
)
d
2
Y
(
y
)
d
y
2
=
C
{\displaystyle {\frac {1}{Y(y)}}\ {\frac {\mathrm {d} ^{2}Y(y)}{\mathrm {d} y^{2}}}=C}
1
Z
(
z
)
d
2
Z
(
z
)
d
z
2
=
−
C
{\displaystyle {\frac {1}{Z(z)}}\ {\frac {\mathrm {d} ^{2}Z(z)}{\mathrm {d} z^{2}}}=-C}
這樣，一個二次偏微分方程式被改變為兩個簡單的二次常微分方程式。解答分別為
Y
(
y
)
=
A
1
e
i
k
y
+
A
2
e
−
i
k
y
{\displaystyle Y(y)=A_{1}e^{iky}+A_{2}e^{-iky}}
Z
(
z
)
=
B
1
e
k
z
+
B
2
e
−
k
z
{\displaystyle Z(z)=B_{1}e^{kz}+B_{2}e^{-kz}}
其中，
A
1
(
k
)
{\displaystyle A_{1}(k)}
A
2
(
k
)
{\displaystyle A_{2}(k)}
B
1
(
k
)
{\displaystyle B_{1}(k)}
B
2
(
k
)
{\displaystyle B_{2}(k)}
當
z
{\displaystyle z}
Z
(
z
)
{\displaystyle Z(z)}
B
1
=
0
{\displaystyle B_{1}=0}
ϕ
(
y
,
z
)
=
∫
0
∞
(
A
1
e
i
k
y
+
A
2
e
−
i
k
y
)
e
−
k
z
d
k
{\displaystyle \phi (y,z)=\int _{0}^{\infty }(A_{1}e^{iky}+A_{2}e^{-iky})e^{-kz}\mathrm {d} k}
由於在
z
=
0
{\displaystyle z=0}
+ 、y- -半平面的電勢分別為
+
V
{\displaystyle +V}
−
V
{\displaystyle -V}
當
y
>
0
{\displaystyle y>0}
∫
0
∞
(
A
1
e
i
k
y
+
A
2
e
−
i
k
y
)
d
k
=
+
V
{\displaystyle \int _{0}^{\infty }(A_{1}e^{iky}+A_{2}e^{-iky})\mathrm {d} k=+V}
當
y
<
0
{\displaystyle y<0}
∫
0
∞
(
A
1
e
i
k
y
+
A
2
e
−
i
k
y
)
d
k
=
−
V
{\displaystyle \int _{0}^{\infty }(A_{1}e^{iky}+A_{2}e^{-iky})\mathrm {d} k=-V}
應用傅立葉變換，可以得到
A
1
(
k
)
=
V
2
π
(
∫
0
∞
e
−
i
k
y
′
d
y
′
−
∫
−
∞
0
e
−
i
k
y
′
d
y
′
)
{\displaystyle A_{1}(k)={\frac {V}{2\pi }}\left(\int _{0}^{\infty }e^{-iky'}\mathrm {d} y'-\int _{-\infty }^{0}e^{-iky'}\mathrm {d} y'\right)}
A
2
(
k
)
=
V
2
π
(
∫
0
∞
e
i
k
y
′
d
y
′
−
∫
−
∞
0
e
i
k
y
′
d
y
′
)
{\displaystyle A_{2}(k)={\frac {V}{2\pi }}\left(\int _{0}^{\infty }e^{iky'}\mathrm {d} y'-\int _{-\infty }^{0}e^{iky'}\mathrm {d} y'\right)}
所以，由
A
1
(
k
)
{\displaystyle A_{1}(k)}
ϕ
1
=
V
2
π
∫
0
∞
d
k
{
∫
0
∞
e
i
k
(
y
−
y
′
)
−
k
z
d
y
′
−
∫
−
∞
0
e
i
k
(
y
−
y
′
)
−
k
z
d
y
′
}
=
−
V
2
π
∫
0
∞
d
y
′
i
(
y
−
y
′
)
−
z
+
V
2
π
∫
−
∞
0
d
y
′
i
(
y
−
y
′
)
−
z
{\displaystyle {\begin{aligned}\phi _{1}&={\frac {V}{2\pi }}\int _{0}^{\infty }\mathrm {d} k\left\{\int _{0}^{\infty }e^{ik(y-y')-kz}\mathrm {d} y'-\int _{-\infty }^{0}e^{ik(y-y')-kz}\mathrm {d} y'\right\}\\&=-\ {\frac {V}{2\pi }}\int _{0}^{\infty }{\frac {\mathrm {d} y'}{i(y-y')-z}}+\ {\frac {V}{2\pi }}\int _{-\infty }^{0}{\frac {\mathrm {d} y'}{i(y-y')-z}}\\\end{aligned}}}
。 類似地，由
A
2
(
k
)
{\displaystyle A_{2}(k)}
ϕ
2
=
V
2
π
∫
0
∞
d
k
{
∫
0
∞
e
−
i
k
(
y
−
y
′
)
−
k
z
d
y
′
−
∫
−
∞
0
e
−
i
k
(
y
−
y
′
)
−
k
z
d
y
′
}
=
−
V
2
π
∫
0
∞
d
y
′
−
i
(
y
−
y
′
)
−
z
+
V
2
π
∫
−
∞
0
d
y
′
−
i
(
y
−
y
′
)
−
z
{\displaystyle {\begin{aligned}\phi _{2}&={\frac {V}{2\pi }}\int _{0}^{\infty }\mathrm {d} k\left\{\int _{0}^{\infty }e^{-ik(y-y')-kz}\mathrm {d} y'-\int _{-\infty }^{0}e^{-ik(y-y')-kz}\mathrm {d} y'\right\}\\&=-\ {\frac {V}{2\pi }}\int _{0}^{\infty }{\frac {\mathrm {d} y'}{-i(y-y')-z}}+\ {\frac {V}{2\pi }}\int _{-\infty }^{0}{\frac {\mathrm {d} y'}{-i(y-y')-z}}\\\end{aligned}}}
。 總電勢為[ 4]
ϕ
=
V
z
π
∫
0
∞
d
y
′
(
y
−
y
′
)
2
+
z
2
−
V
z
π
∫
−
∞
0
d
y
′
(
y
−
y
′
)
2
+
z
2
=
2
V
π
arctan
(
y
z
)
{\displaystyle {\begin{aligned}\phi &={\frac {Vz}{\pi }}\int _{0}^{\infty }{\frac {\mathrm {d} y'}{(y-y')^{2}+z^{2}}}-\ {\frac {Vz}{\pi }}\int _{-\infty }^{0}{\frac {\mathrm {d} y'}{(y-y')^{2}+z^{2}}}\\&={\frac {2V}{\pi }}\ \arctan {\left({\frac {y}{z}}\right)}\\\end{aligned}}}
。
包括函數
1
/
|
r
−
r
′
|
{\displaystyle 1/|\mathbf {r} -\mathbf {r} '|}
G
(
r
,
r
′
)
{\displaystyle G(\mathbf {r} ,\mathbf {r} ')}
格林函數 ，能夠滿足方程式
∇
2
G
(
r
,
r
′
)
=
−
4
π
δ
(
r
−
r
′
)
{\displaystyle \nabla ^{2}G(\mathbf {r} ,\mathbf {r} ')=-4\pi \delta (\mathbf {r} -\mathbf {r} ')}
另外，假設函數
H
(
r
,
r
′
)
{\displaystyle H(\mathbf {r} ,\mathbf {r} ')}
∇
2
H
(
r
,
r
′
)
=
0
{\displaystyle \nabla ^{2}H(\mathbf {r} ,\mathbf {r} ')=0}
則函數
G
′
(
r
,
r
′
)
=
G
(
r
,
r
′
)
+
H
(
r
,
r
′
)
{\displaystyle G'(\mathbf {r} ,\mathbf {r} ')=G(\mathbf {r} ,\mathbf {r} ')+H(\mathbf {r} ,\mathbf {r} ')}
應用這靈活性質，可以更嚴格地規定格林函數：[ 5]
對於狄利克雷問題 ，當源位置
r
′
{\displaystyle \mathbf {r} '}
S
′
{\displaystyle {\mathbb {S} '}}
G
D
(
r
,
r
′
)
=
0
{\displaystyle G_{D}(\mathbf {r} ,\mathbf {r} ')=0}
ϕ
(
r
′
)
{\displaystyle \phi (\mathbf {r} ')}
r
′
{\displaystyle \mathbf {r} '}
ψ
(
r
,
r
′
)
=
G
D
(
r
,
r
′
)
{\displaystyle \psi (\mathbf {r} ,\mathbf {r} ')=G_{D}(\mathbf {r} ,\mathbf {r} ')}
ϕ
(
r
)
=
1
4
π
ϵ
0
∫
V
′
ρ
(
r
′
)
G
D
(
r
,
r
′
)
d
3
r
′
−
1
4
π
∮
S
′
ϕ
(
r
′
)
∂
G
D
(
r
,
r
′
)
∂
n
′
d
2
r
′
{\displaystyle \phi (\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\int _{\mathbb {V} '}\rho (\mathbf {r} ')G_{D}(\mathbf {r} ,\mathbf {r} ')\ \mathrm {d} ^{3}r'-\ {\frac {1}{4\pi }}\oint _{\mathbb {S} '}\phi (\mathbf {r} ')\ {\partial G_{D}(\mathbf {r} ,\mathbf {r} ') \over \partial n'}\mathrm {d} ^{2}r'}
（2） 對於滿足紐曼問題 ，當源位置
r
′
{\displaystyle \mathbf {r} '}
S
′
{\displaystyle {\mathbb {S} '}}
∮
S
′
∂
G
D
(
r
,
r
′
)
∂
n
′
d
2
r
′
=
−
4
π
S
{\displaystyle \oint _{\mathbb {S} '}{\frac {\partial G_{D}(\mathbf {r} ,\mathbf {r} ')}{\partial n'}}\mathrm {d} ^{2}r'=-{\frac {4\pi }{S}}}
這兩種規定都能夠唯一地設定格林函數。注意到格林函數是一個幾何函數，與整個系統的電荷分佈無關。對於任何系統，只要計算出適合其幾何形狀的格林函數，則不論系統的電荷分佈為何，都可以使用同樣的格林函數。
位於xy-平面的是一個接地 的無限平面導體。其上方的點電荷
q
{\displaystyle q}
(
0
,
0
,
a
)
{\displaystyle (0,\,0,\,a)}
假設xy-平面是接地 的無限平面導體 ，則對於z+ 半空間、滿足狄利克雷邊界條件的格林函數為
G
D
(
r
,
r
′
)
=
1
(
x
−
x
′
)
2
+
(
y
−
y
′
)
2
+
(
z
−
z
′
)
2
−
1
(
x
−
x
′
)
2
+
(
y
−
y
′
)
2
+
(
z
+
z
′
)
2
{\displaystyle {\begin{matrix}G_{D}(\mathbf {r} ,\mathbf {r} ')={\cfrac {1}{\sqrt {(x-x')^{2}+(y-y')^{2}+(z-z')^{2}}}}\\\qquad \qquad \qquad -\ {\cfrac {1}{\sqrt {(x-x')^{2}+(y-y')^{2}+(z+z')^{2}}}}\\\end{matrix}}}
； 其中，
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
(
x
′
,
y
′
,
z
′
)
{\displaystyle (x',y',z')}
r
{\displaystyle \mathbf {r} }
r
′
{\displaystyle \mathbf {r} '}
直角坐標 。
由於接地導體的電勢為零，方程式（2）的面積分項目等於零，方程式（2）變為
ϕ
(
r
)
=
1
4
π
ϵ
0
∫
V
′
ρ
(
r
′
)
G
D
(
r
,
r
′
)
d
3
r
′
{\displaystyle \phi (\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\int _{\mathbb {V} '}\rho (\mathbf {r} ')G_{D}(\mathbf {r} ,\mathbf {r} ')\ \mathrm {d} ^{3}r'}
假設在位置
(
0
,
0
,
a
)
{\displaystyle (0,0,a)}
q
{\displaystyle q}
+ 半空間任意位置的電勢為
ϕ
(
r
)
=
1
4
π
ϵ
0
∫
V
′
ρ
(
r
′
)
(
1
x
2
+
y
2
+
(
z
−
a
)
2
−
1
x
2
+
y
2
+
(
z
+
a
)
2
)
d
3
r
′
=
1
4
π
ϵ
0
(
q
x
2
+
y
2
+
(
z
−
a
)
2
−
q
x
2
+
y
2
+
(
z
+
a
)
2
)
{\displaystyle {\begin{aligned}\phi (\mathbf {r} )&={\frac {1}{4\pi \epsilon _{0}}}\int _{\mathbb {V} '}\rho (\mathbf {r} ')\left({\frac {1}{\sqrt {x^{2}+y^{2}+(z-a)^{2}}}}-{\frac {1}{\sqrt {x^{2}+y^{2}+(z+a)^{2}}}}\right)\ \mathrm {d} ^{3}r'\\&={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q}{\sqrt {x^{2}+y^{2}+(z-a)^{2}}}}-{\frac {q}{\sqrt {x^{2}+y^{2}+(z+a)^{2}}}}\right)\\\end{aligned}}}
。 仔細檢察這方程式，右手邊第一個項目，是在沒有平面導體的狀況時，點電荷
q
{\displaystyle q}
鏡像法 時，鏡像電荷
−
q
{\displaystyle -q}
鏡像法 條目的點電荷與無限平面導體 段落。
已知函數
1
/
|
r
−
r
′
|
{\displaystyle 1/|\mathbf {r} -\mathbf {r} '|}
G
(
r
,
r
′
)
{\displaystyle G(\mathbf {r} ,\mathbf {r} ')}
∇
2
G
(
r
,
r
′
)
=
−
4
π
δ
(
r
−
r
′
)
{\displaystyle \nabla ^{2}G(\mathbf {r} ,\mathbf {r} ')=-4\pi \delta (\mathbf {r} -\mathbf {r} ')}
在三維無限空間裏，
1
/
|
r
−
r
′
|
{\displaystyle 1/|\mathbf {r} -\mathbf {r} '|}
傅立葉級數 為[ 6]
1
|
r
−
r
′
|
≡
1
2
π
2
∫
−
∞
∞
∫
−
∞
∞
∫
−
∞
∞
d
3
k
e
i
k
⋅
(
r
−
r
′
)
k
2
=
1
2
π
2
∫
−
∞
∞
∫
−
∞
∞
d
k
x
d
k
y
e
i
k
x
(
x
−
x
′
)
+
i
k
y
(
y
−
y
′
)
∫
−
∞
∞
d
k
z
e
i
k
z
(
z
−
z
′
)
k
x
2
+
k
y
2
+
k
z
2
{\displaystyle {\begin{aligned}{\frac {1}{|\mathbf {r} -\mathbf {r} '|}}&\equiv {\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\mathrm {d} ^{3}k{\frac {e^{i\mathbf {k} \cdot (\mathbf {r} -\mathbf {r} ')}}{k^{2}}}\\&={\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\mathrm {d} k_{x}\ \mathrm {d} k_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty }^{\infty }\ \mathrm {d} k_{z}{\frac {e^{ik_{z}(z-z')}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}\\\end{aligned}}}
。 現在，必需找到格林函數
G
D
(
r
,
r
′
)
=
G
(
r
,
r
′
)
+
H
(
r
,
r
′
)
{\displaystyle G_{D}(\mathbf {r} ,\mathbf {r} ')=G(\mathbf {r} ,\mathbf {r} ')+H(\mathbf {r} ,\mathbf {r} ')}
G
D
(
(
x
,
y
,
0
)
,
r
′
)
=
0
{\displaystyle G_{D}((x,y,0),\mathbf {r} ')=0}
H
(
r
,
r
′
)
{\displaystyle H(\mathbf {r} ,\mathbf {r} ')}
∇
2
H
(
r
,
r
′
)
=
0
{\displaystyle \nabla ^{2}H(\mathbf {r} ,\mathbf {r} ')=0}
對於z+ 半空間，
H
(
r
,
r
′
)
{\displaystyle H(\mathbf {r} ,\mathbf {r} ')}
傅立葉級數 擴張為
H
(
r
,
r
′
)
=
1
2
π
2
∫
−
∞
∞
∫
−
∞
∞
d
k
x
d
k
y
e
i
k
x
(
x
−
x
′
)
+
i
k
y
(
y
−
y
′
)
∫
−
∞
∞
d
k
z
[
B
(
k
,
z
′
)
e
i
k
z
z
+
C
(
k
,
z
′
)
e
−
i
k
z
z
]
{\displaystyle {\begin{aligned}H(\mathbf {r} ,\mathbf {r} ')&={\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ \mathrm {d} k_{x}\ \mathrm {d} k_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty }^{\infty }\ \mathrm {d} k_{z}\left[B(\mathbf {k} ,z')e^{ik_{z}z}+C(\mathbf {k} ,z')e^{-ik_{z}z}\right]\\\end{aligned}}}
對於x-座標與對於y-座標的傅立葉級數 擴張，
H
{\displaystyle H}
G
{\displaystyle G}
H
{\displaystyle H}
G
D
(
r
,
r
′
)
{\displaystyle G_{D}(\mathbf {r} ,\mathbf {r} ')}
G
D
(
r
,
r
′
)
=
1
2
π
2
∫
−
∞
∞
∫
−
∞
∞
d
k
x
d
k
y
e
i
k
x
(
x
−
x
′
)
+
i
k
y
(
y
−
y
′
)
∫
−
∞
∞
d
k
z
[
e
i
k
z
(
z
−
z
′
)
k
x
2
+
k
y
2
+
k
z
2
+
B
(
k
,
z
′
)
e
i
k
z
z
+
C
(
k
,
z
′
)
e
−
i
k
z
z
]
{\displaystyle G_{D}(\mathbf {r} ,\mathbf {r} ')={\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ \mathrm {d} k_{x}\ \mathrm {d} k_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty }^{\infty }\ \mathrm {d} k_{z}\left[{\frac {e^{ik_{z}(z-z')}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}+B(\mathbf {k} ,z')e^{ik_{z}z}+C(\mathbf {k} ,z')e^{-ik_{z}z}\right]}
其中，
B
(
k
,
z
′
)
{\displaystyle B(\mathbf {k} ,z')}
C
(
k
,
z
′
)
{\displaystyle C(\mathbf {k} ,z')}
由於
G
D
(
(
x
,
y
,
0
)
,
r
′
)
=
0
{\displaystyle G_{D}((x,y,0),\mathbf {r} ')=0}
k
{\displaystyle \mathbf {k} }
z
′
{\displaystyle z'}
B
(
k
,
z
′
)
{\displaystyle B(\mathbf {k} ,z')}
C
(
k
,
z
′
)
{\displaystyle C(\mathbf {k} ,z')}
e
−
i
k
z
z
′
k
x
2
+
k
y
2
+
k
z
2
+
B
(
k
,
z
′
)
+
C
k
,
z
′
)
=
0
{\displaystyle {\frac {e^{-ik_{z}z'}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}+B(\mathbf {k} ,z')+C\mathbf {k} ,z')=0}
B
(
k
,
z
′
)
=
B
0
e
−
i
k
z
z
′
k
x
2
+
k
y
2
+
k
z
2
{\displaystyle B(\mathbf {k} ,z')={\frac {B_{0}e^{-ik_{z}z'}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}}
C
(
k
,
z
′
)
=
C
0
e
−
i
k
z
z
′
k
x
2
+
k
y
2
+
k
z
2
{\displaystyle C(\mathbf {k} ,z')={\frac {C_{0}e^{-ik_{z}z'}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}}
其中，
B
0
{\displaystyle B_{0}}
C
0
{\displaystyle C_{0}}
B
0
+
C
0
=
−
1
{\displaystyle B_{0}+C_{0}=-1}
將這些公式代入
G
D
{\displaystyle G_{D}}
G
D
(
r
,
r
′
)
=
1
2
π
2
∫
−
∞
∞
∫
−
∞
∞
d
k
x
d
k
y
e
i
k
x
(
x
−
x
′
)
+
i
k
y
(
y
−
y
′
)
∫
−
∞
∞
d
k
z
{
(
1
+
B
0
)
k
2
[
e
i
k
z
(
z
−
z
′
)
−
e
i
k
z
(
z
+
z
′
)
]
}
{\displaystyle G_{D}(\mathbf {r} ,\mathbf {r} ')={\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ \mathrm {d} k_{x}\ \mathrm {d} k_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty }^{\infty }\ \mathrm {d} k_{z}\left\{{\frac {(1+B_{0})}{k^{2}}}\left[e^{ik_{z}(z-z')}-e^{ik_{z}(z+z')}\right]\right\}}
為了滿足方程式
∇
2
G
D
(
r
,
r
′
)
=
−
4
π
δ
(
r
−
r
′
)
{\displaystyle \nabla ^{2}G_{D}(\mathbf {r} ,\mathbf {r} ')=-4\pi \delta (\mathbf {r} -\mathbf {r} ')}
B
0
=
0
{\displaystyle B_{0}=0}
G
D
(
r
,
r
′
)
=
1
2
π
2
∫
−
∞
∞
∫
−
∞
∞
d
k
x
d
k
y
e
i
k
x
(
x
−
x
′
)
+
i
k
y
(
y
−
y
′
)
∫
−
∞
∞
d
k
z
{
1
k
2
[
e
i
k
z
(
z
−
z
′
)
−
e
i
k
z
(
z
+
z
′
)
]
}
=
1
|
r
−
r
′
|
−
1
|
r
−
r
″
|
=
1
(
x
−
x
′
)
2
+
(
y
−
y
′
)
2
+
(
z
−
z
′
)
2
−
1
(
x
−
x
′
)
2
+
(
y
−
y
′
)
2
+
(
z
+
z
′
)
2
{\displaystyle {\begin{aligned}G_{D}(\mathbf {r} ,\mathbf {r} ')&={\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ \mathrm {d} k_{x}\ \mathrm {d} k_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty }^{\infty }\ \mathrm {d} k_{z}\left\{{\frac {1}{k^{2}}}\left[e^{ik_{z}(z-z')}-e^{ik_{z}(z+z')}\right]\right\}\\&={\frac {1}{|\mathbf {r} -\mathbf {r} '|}}-{\frac {1}{|\mathbf {r} -\mathbf {r} ''|}}\\&={\cfrac {1}{\sqrt {(x-x')^{2}+(y-y')^{2}+(z-z')^{2}}}}-\ {\cfrac {1}{\sqrt {(x-x')^{2}+(y-y')^{2}+(z+z')^{2}}}}\\\end{aligned}}}
； 其中，
r
″
=
(
x
′
,
y
′
,
−
z
′
)
{\displaystyle \mathbf {r} ''=(x',y',-z')}
電勢 . 中華語文知識庫. [2016-03-03 ] . （原始內容 存檔於2016年3月6日） （中文（中國大陸）） .Halliday, David; Robert Resnick, Jearl Walker, Fundamental of Physics 7th, USA: John Wiley and Sons, Inc.: pp. 630ff, 2005, ISBN 0-471-23231-9 Beyer, William, CRC Standard Mathematical Table 28th, CRC Press, 1987, ISBN 0-8493-0628-0 pp. 241, formula #43,
pp. 252, formula#165Griffiths, David J. Introduction to Electrodynamics 3rd. Prentice Hall. 1998: pp. 555–557. ISBN 0-13-805326-X 
![{\displaystyle \int _{\mathbb {V} '}\left[\phi (\mathbf {r} ')\nabla ^{2}\left({\frac {1}{|\mathbf {r} -\mathbf {r} '|}}\right)+{\frac {\rho (\mathbf {r} ')}{\epsilon _{0}|\mathbf {r} -\mathbf {r} '|}}\right]\mathrm {d} ^{3}r'=\oint _{\mathbb {S} '}\left[\phi \ {\partial \over \partial n'}\left({\frac {1}{|\mathbf {r} -\mathbf {r} '|}}\right)-\left({\frac {1}{|\mathbf {r} -\mathbf {r} '|}}\right){\partial \phi \over \partial n'}\right]\mathrm {d} ^{2}r'}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4d85701a95584dce0f1b57fb08b286a71b808a8b)
![{\displaystyle \phi (\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\int _{\mathbb {V} '}{\frac {\rho (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}\ \mathrm {d} ^{3}r'+{\frac {1}{4\pi }}\oint _{\mathbb {S} '}\left[\left({\frac {1}{|\mathbf {r} -\mathbf {r} '|}}\right){\partial \phi \over \partial n'}-\phi \ {\partial \over \partial n'}\left({\frac {1}{|\mathbf {r} -\mathbf {r} '|}}\right)\right]\mathrm {d} ^{2}r'}](http://wikimedia.org/api/rest_v1/media/math/render/svg/264d760bfb803dd1dd72fb799e39894c6b02c15f)
![{\displaystyle {\begin{aligned}H(\mathbf {r} ,\mathbf {r} ')&={\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ \mathrm {d} k_{x}\ \mathrm {d} k_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty }^{\infty }\ \mathrm {d} k_{z}\left[B(\mathbf {k} ,z')e^{ik_{z}z}+C(\mathbf {k} ,z')e^{-ik_{z}z}\right]\\\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/67ffb34ffce09728c29b62ab5b3866c46d933589)
![{\displaystyle G_{D}(\mathbf {r} ,\mathbf {r} ')={\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ \mathrm {d} k_{x}\ \mathrm {d} k_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty }^{\infty }\ \mathrm {d} k_{z}\left[{\frac {e^{ik_{z}(z-z')}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}+B(\mathbf {k} ,z')e^{ik_{z}z}+C(\mathbf {k} ,z')e^{-ik_{z}z}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/276d3e7d2d0545641910018550914f08e2668426)
![{\displaystyle G_{D}(\mathbf {r} ,\mathbf {r} ')={\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ \mathrm {d} k_{x}\ \mathrm {d} k_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty }^{\infty }\ \mathrm {d} k_{z}\left\{{\frac {(1+B_{0})}{k^{2}}}\left[e^{ik_{z}(z-z')}-e^{ik_{z}(z+z')}\right]\right\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4bca583931500f44b518700a7408200f11bfb31d)
![{\displaystyle {\begin{aligned}G_{D}(\mathbf {r} ,\mathbf {r} ')&={\frac {1}{2\pi ^{2}}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ \mathrm {d} k_{x}\ \mathrm {d} k_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty }^{\infty }\ \mathrm {d} k_{z}\left\{{\frac {1}{k^{2}}}\left[e^{ik_{z}(z-z')}-e^{ik_{z}(z+z')}\right]\right\}\\&={\frac {1}{|\mathbf {r} -\mathbf {r} '|}}-{\frac {1}{|\mathbf {r} -\mathbf {r} ''|}}\\&={\cfrac {1}{\sqrt {(x-x')^{2}+(y-y')^{2}+(z-z')^{2}}}}-\ {\cfrac {1}{\sqrt {(x-x')^{2}+(y-y')^{2}+(z+z')^{2}}}}\\\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/68ab02614b77010f741d6302b3df313fd8b9d117)
![{\displaystyle {\begin{aligned}{\partial G_{D} \over \partial n'}&=-\ {\partial G_{D} \over \partial z'}\\&=-\ {\cfrac {z-z'}{[(x-x')^{2}+(y-y')^{2}+(z-z')^{2}]^{3/2}}}\ -\ {\cfrac {z+z'}{[(x-x')^{2}+(y-y')^{2}+(z+z')^{2}]^{3/2}}}\\&=-\ {\cfrac {2z}{[(x-x')^{2}+(y-y')^{2}+z^{2}]^{3/2}}}\\\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/75afc05c54454b72455434245d4b8bd27a893391)
![{\displaystyle {\begin{aligned}\phi (\mathbf {r} )&={\frac {2z}{4\pi }}\left\{\int _{0+}^{\infty }\int _{-\infty }^{\infty }{\cfrac {V\mathrm {d} x'\mathrm {d} y'}{[(x-x')^{2}+(y-y')^{2}+z^{2}]^{3/2}}}+\int _{-\infty }^{0-}\int _{-\infty }^{\infty }{\cfrac {-V\mathrm {d} x'\mathrm {d} y'}{[(x-x')^{2}+(y-y')^{2}+z^{2}]^{3/2}}}\right\}\\&=\ {\frac {zV}{\pi }}\left\{\int _{0+}^{\infty }{\frac {\mathrm {d} y'}{(y-y')^{2}+z^{2}}}-\int _{-\infty }^{0-}{\frac {\mathrm {d} y'}{(y-y')^{2}+z^{2}}}\right\}\\&={\frac {2V}{\pi }}\ \arctan {\left({\frac {y}{z}}\right)}\\\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b8cabe883bcda4043675000bf274c893cdd89935)
