自然對數

自然對數（英語：Natural logarithm）為以數學常數e為底數的對數函數，標記作${\displaystyle \ln x}$或${\displaystyle \log _{e}x}$，其反函數為指數函數${\displaystyle e^{x}}$。^{[註 1]}

自然對數${\displaystyle \ln(x)}$的函數圖像

自然對數${\displaystyle \ln(x)}$的積分定義

自然對數積分定義為對任何正實數${\displaystyle x}$，由${\displaystyle 1}$到${\displaystyle x}$所圍成，${\displaystyle xy=1}$曲線下的面積。如果${\displaystyle x}$小於1，則計算面積為負數。

${\displaystyle \ln x=\int _{1}^{x}{\frac {dt}{t}}\,}$

${\displaystyle e}$則定義為唯一的實數${\displaystyle x}$使得${\displaystyle \ln x=1}$。

自然對數一般表示為${\displaystyle \ln x\!}$，數學中亦有以${\displaystyle \log x\!}$表示自然對數。^{[1][註 2]}

歷史

十七世紀

雙曲線扇形是笛卡爾平面${\displaystyle \{(x,y)\}}$上的一個區域，由從原點到${\textstyle (a,{\frac {1}{a}})}$和${\textstyle (b,{\frac {1}{b}})}$的射線，以及雙曲線${\displaystyle xy=1}$圍成。在標準位置的雙曲線扇形有${\displaystyle a=1}$且${\displaystyle b>1}$，它的面積為${\displaystyle \ln(b)}$^[2]，此時雙曲線扇形對應正雙曲角。

當直角雙曲線下的兩段面積相等時，${\displaystyle x}$的值呈等比數列，${\textstyle {\frac {x_{2}}{x_{1}}}={\frac {x_{1}}{x_{0}}}=k}$，${\displaystyle y}$的值也呈等比數列，${\textstyle {\frac {x_{2}}{x_{1}}}={\frac {x_{1}}{x_{0}}}={\frac {1}{k}}}$。

約翰·納皮爾在1614年^[3]以及約斯特·比爾吉在6年後^[4]，分別發表了獨立編制的對數表，當時通過對接近1的底數的大量乘冪運算，來找到指定範圍和精度的對數和所對應的真數。當時還沒出現有理數冪的概念，按後世的觀點，約翰·納皮爾的底數0.9999999^10000000相當接近${\textstyle {\frac {1}{e}}}$^[5]，而約斯特·比爾吉的底數1.0001¹⁰⁰⁰⁰相當接近自然對數的底數${\displaystyle e}$。實際上不需要做開高次方這種艱難運算，約翰·納皮爾用了20年時間進行相當於數百萬次乘法的計算，亨利·布里格斯（英語：Henry Briggs (mathematician)）建議納皮爾改用10為底數未果，他用自己的方法^[6]於1624年部份完成了常用對數表的編制。

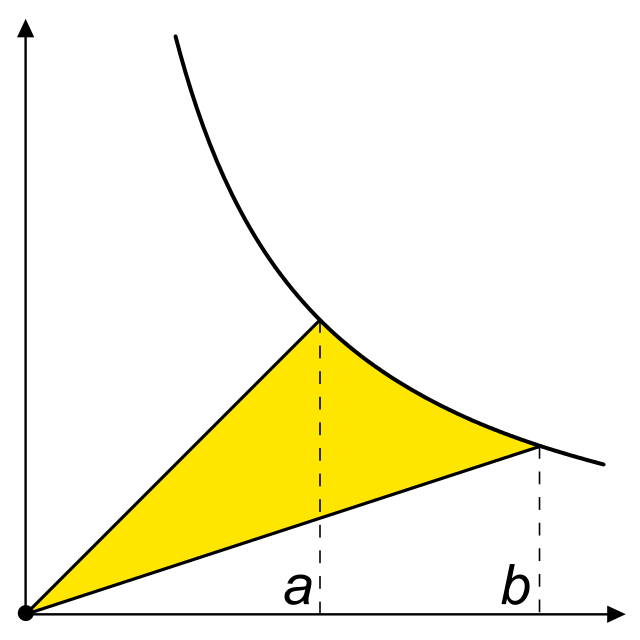
形如${\displaystyle f(x)=x^{p}}$的曲線都有一個代數反導數，除了特殊情況${\displaystyle p=-1}$對應於雙曲線的弓形面積（英語：Quadrature (mathematics)），即雙曲線扇形；其他情況都由1635年發表的卡瓦列里弓形面積公式（英語：Cavalieri's quadrature formula）給出^[7]，其中拋物線的弓形面積由公元前3世紀的阿基米德完成（拋物線的弓形面積），雙曲線的弓形面積需要發明一個新函數。1647年聖文森特的格列高利（英語：Grégoire de Saint-Vincent）將對數聯繫於雙曲線${\displaystyle xy=1}$的弓形面積，他發現x軸上${\displaystyle [a,b]}$兩點對應的雙曲線線段與原點圍成的雙曲線扇形同${\displaystyle [c,d]}$對應的扇形，在${\textstyle {\frac {a}{b}}={\frac {c}{d}}}$時面積相同，這指出了雙曲線從${\displaystyle x=1}$到${\displaystyle x=t}$的積分${\displaystyle f(t)}$滿足^[8]：

${\displaystyle f(tu)=f(t)+f(u)\,}$

1649年，薩拉薩的阿爾豐斯·安東尼奧（英語：Alphonse Antonio de Sarasa）將雙曲線下的面積解釋為對數。大約1665年，伊薩克·牛頓推廣了二項式定理，他將${\textstyle {\frac {1}{1+x}}}$展開並逐項積分，得到了自然對數的無窮級數。「自然對數」最早描述見於尼古拉斯·麥卡托在1668年出版的著作《Logarithmotechnia》中^[9]，他也獨立發現了同樣的級數，即自然對數的麥卡托級數。

十八世紀

大約1730年，歐拉定義互為逆函數的指數函數和自然對數為^[10][11]：

${\displaystyle e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n},}$

${\displaystyle \ln(x)=\lim _{n\rightarrow \infty }n\left(x^{\frac {1}{n}}-1\right)}$

1742年威廉·瓊斯發表了現在的冪指數概念^[12]。

形式定義

歐拉定義自然對數為序列的極限：

${\displaystyle \ln(x)=\lim _{n\rightarrow \infty }n\left(x^{\frac {1}{n}}-1\right).}$

${\displaystyle \ln(a)}$正式定義為積分，

${\displaystyle \ln(a)=\int _{1}^{a}{\frac {1}{x}}\,dx.}$

這個函數為對數是因滿足對數的基本性質:

${\displaystyle \ln(ab)=\ln(a)+\ln(b).\,\!}$

這可以通過將定義了${\displaystyle \ln(ab)}$的積分拆分為兩部份，並在第二部份中進行換元${\displaystyle x=ta}$來證實:

${\displaystyle \ln(ab)=\int _{1}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{a}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{at}}\;d(at)}$

${\displaystyle =\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{t}}\;dt=\ln(a)+\ln(b).}$

冪公式${\displaystyle \ln(t^{r})=r\ln(t)}$可如下推出:

${\displaystyle \ln(t^{r})=\int _{1}^{t^{r}}{\frac {1}{x}}dx=\int _{1}^{t}{\frac {1}{u^{r}}}d\left(u^{r}\right)=\int _{1}^{t}{\frac {1}{u^{r}}}\left(ru^{r-1}\,du\right)=r\int _{1}^{t}{\frac {1}{u}}\,du=r\ln(t).}$

第二個等式使用了換元${\displaystyle u=x^{\frac {1}{r}}}$。

自然對數還有在某些情況下更有用的另一個積分表示：

${\displaystyle \ln(x)=-\lim _{\epsilon \to 0}\int _{\epsilon }^{\infty }{\frac {dt}{t}}\left(e^{-xt}-e^{-t}\right).}$

性質

• ${\displaystyle \ln(1)=\int _{1}^{1}{\frac {1}{t}}\,dt=0\,}$
• ${\displaystyle \operatorname {ln} (-1)=i\pi \,}$

(參見複數對數)

• ${\displaystyle \ln(x)<\ln(y)\quad {\rm {for}}\quad 0<x<y\,}$
• ${\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1\,}$
• ${\displaystyle \ln(x^{y})=y\,\ln(x)\,}$
• ${\displaystyle {\frac {x-1}{x}}\leq \ln(x)\leq x-1\quad {\rm {for}}\quad x>0\,}$
• ${\displaystyle \ln {(1+x^{\alpha })}\leq \alpha x\quad {\rm {for}}\quad x\geq 0,\alpha \geq 1\,}$

證明
${\displaystyle \lim _{h\to 0}{\frac {\ln(1+h)}{h}}=\lim _{h\to 0}{\frac {\ln(1+h)-\ln 1}{h}}={\frac {d}{dx}}\ln x{\Bigg |}_{x=1}=1}$

導數

自然對數的圖像和它在${\displaystyle x=1.5}$處的切線。

${\displaystyle \ln(1+x)}$的泰勒多項式只在${\displaystyle -1<x\leq 1}$範圍內有逐步精確的近似。

自然對數的導數為

${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}.\,}$

證明一（微積分第一基本定理）:${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {d}{dx}}\int _{1}^{x}{\frac {1}{t}}\,dt={\frac {1}{x}}}$

證明二：按此影片（頁面存檔備份，存於互聯網檔案館）

${\displaystyle {\frac {d}{dx}}\ln(x)=\lim _{h\to 0}{\frac {\ln(x+h)-\ln(x)}{h}}}$

${\displaystyle =\lim _{h\to 0}{\frac {\ln({\frac {x+h}{x}})}{h}}}$

${\displaystyle =\lim _{h\to 0}\left[{\frac {1}{h}}\ln \left(1+{\frac {h}{x}}\right)\right]\quad }$

${\displaystyle =\lim _{h\to 0}\ln \left(1+{\frac {h}{x}}\right)^{\frac {1}{h}}}$

設${\displaystyle u={\frac {h}{x}}\Rightarrow ux=h}$

${\displaystyle {\frac {1}{h}}={\frac {1}{ux}}}$

${\displaystyle {\frac {d}{dx}}\ln(x)=\lim _{u\to 0}\ln(1+u)^{\frac {1}{ux}}}$

${\displaystyle =\lim _{u\to 0}\ln \left[(1+u)^{\frac {1}{u}}\right]^{\frac {1}{x}}}$

${\displaystyle ={\frac {1}{x}}\lim _{u\to 0}\ln(1+u)^{\frac {1}{u}}}$

設${\displaystyle n={\frac {1}{u}}\Rightarrow u={\frac {1}{n}}}$

${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}\lim _{n\to \infty }\ln \left(1+{\frac {1}{n}}\right)^{n}}$

${\displaystyle ={\frac {1}{x}}\ln \left[\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\right]}$

${\displaystyle ={\frac {1}{x}}\ln e}$

${\displaystyle ={\frac {1}{x}}}$

用自然對數定義的更一般的對數函數，${\displaystyle \log _{b}(x)={\frac {\ln(x)}{\ln(b)}}}$，根據其逆函數即一般指數函數的性質，它的導數為^[13][14]：

${\displaystyle {\frac {d}{dx}}\log _{b}(x)={\frac {1}{x\ln(b)}}.}$

根據連鎖法則，以${\displaystyle f(x)}$為參數的自然對數的導數為

${\displaystyle {\frac {d}{dx}}\ln[f(x)]={\frac {f'(x)}{f(x)}}.}$

右手端的商叫做${\displaystyle f}$的對數導數（英語：logarithmic derivative），通過${\displaystyle \ln(f(x))}$的導數的方法計算${\displaystyle f'(x)}$叫做對數微分^[15]。

冪級數

自然對數的導數性質導致了${\displaystyle \ln(1+x)}$在0處的泰勒級數，也叫做麥卡托級數：

${\displaystyle \ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots }$

對於所有${\displaystyle \left|x\right|\leq 1,}$但不包括${\displaystyle x=-1.}$

把${\displaystyle x-1}$代入${\displaystyle x}$中，可得到${\displaystyle \ln(x)}$自身的級數。通過在麥卡托級數上使用歐拉變換，可以得到對絕對值大於1的任何${\displaystyle x}$有效的如下級數:

${\displaystyle \ln {x \over {x-1}}=\sum _{n=1}^{\infty }{1 \over {nx^{n}}}={1 \over x}+{1 \over {2x^{2}}}+{1 \over {3x^{3}}}+\cdots \,.}$

這個級數類似於貝利-波爾溫-普勞夫公式。

還要注意到${\displaystyle x \over {x-1}}$是自身的逆函數，所以要生成特定數${\displaystyle y}$的自然對數，簡單把${\displaystyle x \over {x-1}}$代入${\displaystyle x}$中。

${\displaystyle \ln {x}=\sum _{n=1}^{\infty }{1 \over {n}}\left({x-1 \over x}\right)^{n}=\left({x-1 \over x}\right)+{1 \over 2}\left({x-1 \over x}\right)^{2}+{1 \over 3}\left({x-1 \over x}\right)^{3}+\cdots \,}$

對於${\displaystyle \operatorname {Re} (x)\geq {\frac {1}{2}}\,.}$

自然數的倒數的總和

${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}},}$

叫做調和級數。它與自然對數有密切聯繫：當${\displaystyle n}$趨於無窮的時候，差

${\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}-\ln(n),}$

收斂於歐拉-馬歇羅尼常數。這個關係有助於分析算法比如快速排序的性能。^[16]

積分

自然對數通過分部積分法積分:

${\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C.}$

假設:

${\displaystyle u=\ln(x)\Rightarrow du={\frac {dx}{x}}}$

${\displaystyle dv=dx\Rightarrow v=x\,}$

所以:

${\displaystyle {\begin{aligned}\int \ln(x)\,dx&=x\ln(x)-\int {\frac {x}{x}}\,dx\\&=x\ln(x)-\int 1\,dx\\&=x\ln(x)-x+C\end{aligned}}}$

自然對數可以簡化形如${\displaystyle g(x)={\frac {f'(x)}{f(x)}}}$的函數的積分：${\displaystyle g(x)}$的一個原函數給出為${\displaystyle \ln(\left\vert f(x)\right\vert )}$。這是基於連鎖法則和如下事實:

${\displaystyle \ {d \over dx}\ln \left|x\right|={1 \over x}.}$

換句話說，

${\displaystyle \int {1 \over x}dx=\ln |x|+C}$

且

${\displaystyle \int {{\frac {f'(x)}{f(x)}}\,dx}=\ln |f(x)|+C.}$

例子

下面是${\displaystyle g(x)=\tan x}$的例子：

${\displaystyle {\begin{aligned}\int \tan x\,dx&=\int {\sin x \over \cos x}\,dx\\&=\int {-{d \over dx}\cos x \over {\cos x}}\,dx.\\\end{aligned}}}$

設${\displaystyle f(x)=\cos x}$且${\displaystyle f'(x)=-\sin x}$：

${\displaystyle {\begin{aligned}\int \tan x\,dx&=-\ln {\left|\cos x\right|}+C\\&=\ln {\left|\sec x\right|}+C\\\end{aligned}}}$

與雙曲函數的關係

在直角雙曲線(方程${\displaystyle y={\frac {1}{x}}}$)下，雙曲線三角形(黃色)，和對應於雙曲角${\displaystyle u}$的雙曲線扇形(紅色)。這個三角形的邊分別是雙曲函數中${\displaystyle \cosh }$和${\displaystyle \sinh }$的${\displaystyle {\sqrt {2}}}$倍。

射線出原點交單位雙曲線${\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}$於點${\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}$，這裏的${\displaystyle \scriptstyle a}$是射線、雙曲線和${\displaystyle \scriptstyle x}$軸圍成的面積的二倍。對於雙曲線上位於x軸下方的點，這個面積被認為是負值。

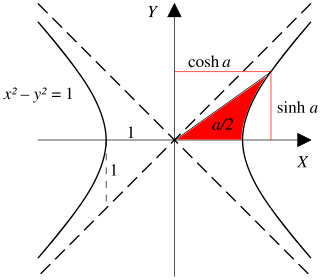
在18世紀，約翰·海因里希·蘭伯特介入雙曲函數^[17]，並計算雙曲幾何中雙曲三角形的面積^[18]。對數函數是在直角雙曲線${\displaystyle xy=1}$下定義的，可構造雙曲線直角三角形，底邊在線${\displaystyle y=x}$上，一個頂點是原點，另一個頂點在雙曲線。這裏以自然對數即雙曲角作為參數的函數，是自然對數的逆函數指數函數，即要形成指定雙曲角${\displaystyle u}$，在漸近線即x或y軸上需要有的${\displaystyle x}$或${\displaystyle y}$的值。顯見這裏的底邊是${\displaystyle \left(e^{u}+e^{-u}\right){\frac {\sqrt {2}}{2}}}$，垂線是${\displaystyle \left(e^{u}-e^{-u}\right){\frac {\sqrt {2}}{2}}}$。

通過旋轉和縮小線性變換，得到單位雙曲線下的情況，有：

• ${\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}}$
• ${\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}}$

單位雙曲線中雙曲線扇形的面積是對應直角雙曲線${\displaystyle xy=1}$下雙曲角的${\displaystyle {\frac {1}{2}}}$。

連分數

儘管自然對數沒有簡單的連分數，但有一些廣義連分數如:

${\displaystyle {\begin{aligned}\ln(1+x)&={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\cdots \\&={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}\\\end{aligned}}}$

${\displaystyle {\begin{aligned}\ln \left(1+{\frac {x}{y}}\right)&={\cfrac {x}{y+{\cfrac {1x}{2+{\cfrac {1x}{3y+{\cfrac {2x}{2+{\cfrac {2x}{5y+{\cfrac {3x}{2+\ddots }}}}}}}}}}}}\\&={\cfrac {2x}{2y+x-{\cfrac {(1x)^{2}}{3(2y+x)-{\cfrac {(2x)^{2}}{5(2y+x)-{\cfrac {(3x)^{2}}{7(2y+x)-\ddots }}}}}}}}\\\end{aligned}}}$

這些連分數特別是最後一個對接近1的值快速收斂。但是，更大的數的自然對數，可以輕易的用這些更小的數的自然對數的加法來計算，帶有類似的快速收斂。

例如，因為${\displaystyle 2=1.25^{3}\times 1.024}$，2的自然對數可以計算為:

${\displaystyle {\begin{aligned}\ln 2&=3\ln \left(1+{\frac {1}{4}}\right)+\ln \left(1+{\frac {3}{125}}\right)\\&={\cfrac {6}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {6}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\\\end{aligned}}}$

進而，因為${\displaystyle 10=1.25^{10}\times 1.024^{3}}$，10的自然對數可以計算為:

${\displaystyle {\begin{aligned}\ln 10&=10\ln \left(1+{\frac {1}{4}}\right)+3\ln \left(1+{\frac {3}{125}}\right)\\&={\cfrac {20}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {18}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\\\end{aligned}}}$

複數對數

主條目：複數對數

指數函數可以擴展為對任何複數${\displaystyle x}$得出複數值為${\displaystyle e^{x}}$的函數，只需要簡單使用${\displaystyle x}$為複數的無窮級數；這個指數函數的逆函數形成複數對數，並帶有正常的對數的多數性質。但是它涉及到了兩個困難：不存在${\displaystyle x}$使得${\displaystyle e^{x}=0}$；並且有着${\displaystyle e^{2\pi i}=1=e^{0}}$。因為乘法性質仍適用於複數指數函數，${\displaystyle e^{z}=e^{z+2n\pi i}}$，對於所有複數${\displaystyle z}$和整數${\displaystyle n}$。

所以對數不能定義在整個複平面上，並且它是多值函數，就是說任何複數對數都可以增加${\displaystyle 2\pi i}$的任何整數倍而成為等價的對數。複數對數只能在切割平面上是單值函數。例如，${\displaystyle \log i={\frac {1}{2}}\pi i}$或${\displaystyle {\frac {5}{2}}\pi i}$或${\displaystyle -{\frac {3}{2}}\pi i}$等等；儘管${\displaystyle i^{4}=1}$，${\displaystyle 4\log =i}$不能定義為${\displaystyle 2\pi i}$或${\displaystyle 10\pi i}$或${\displaystyle -6\pi i}$，以此類推。

• 自然對數函數在複平面（主分支）上的繪圖
• 
  z=Re(ln(x+iy))
• 
• 
• 
  前三圖的疊加

主值定義

對於每個非0複數${\displaystyle z=x+yi}$，主值${\displaystyle \log z}$是虛部位於區間${\displaystyle (-\pi ,\pi ]}$內的對數。表達式${\displaystyle \log 0}$不做定義，因為沒有複數${\displaystyle w}$滿足${\displaystyle e^{w}=0}$。

要對${\displaystyle \log z}$給出一個公式，可以先將${\displaystyle z}$表達為極坐標形式，${\displaystyle z=re^{i\theta }}$。給定${\displaystyle z}$，極坐標形式不是確切唯一的，因為有可能向${\displaystyle \theta }$增加${\displaystyle 2\pi }$的整數倍，所以為了保證唯一性而要求${\displaystyle \theta }$位於區間${\displaystyle (-\pi ,\pi ]}$內；這個${\displaystyle \theta }$叫做幅角的主值，有時寫為${\displaystyle \operatorname {arg} z}$或${\displaystyle \operatorname {atan} 2(y,x)}$。則對數的主值可以定義為^[19] ：

${\displaystyle \operatorname {Log} z:={\text{ln }}r+i\theta =\ln |z|+i\operatorname {Arg} z=\operatorname {ln} {\sqrt {x^{2}+y^{2}}}+i\operatorname {atan2} (y,x).}$

例如，${\displaystyle \operatorname {Log} (-3i)=\ln 3-{\frac {\pi i}{2}}}$。

科學應用

自然指數有應用於表達放射衰變（放射性）之類關於衰減的過程，如放射性原子數目的微分方程${\displaystyle N}$隨時間變化率${\displaystyle {\frac {dN}{dt}}=-pN}$，常數${\displaystyle p}$為原子衰變概率，積分得${\displaystyle N(t)=N(0)\exp(-pt)}$。

註釋

1. 根據微積分學，某函數之定義域為其反函數之值域，反之其值域為其反函數之定義域。因${\displaystyle e^{x}}$的值域為${\displaystyle (0,\infty )}$，且其為${\displaystyle \ln x}$之反函數，故可知${\displaystyle \ln x}$之定義域為${\displaystyle (0,\infty )}$，即${\displaystyle \ln x}$在非正實數系無法定義。
2. 若要避免與底為10的常用對數 ${\displaystyle \log x\!}$ 混淆，可用「全寫」 ${\displaystyle \log _{\boldsymbol {e}}x\!}$ 。

參考資料

1. 例如哈代和賴特所著的《數論入門》"Introduction to the theory of numbers" (1.7, Sixth edition, Oxford 2008)的註解 "log x is, of course the 'Napierian' logarithm of x, to base e. 'Common' logarithms have no mathematical interest."（log x 當然是以e為基，x的「納皮爾」對數。「常用」對數在數學上毫無重要。）
2. 證明：從1到b積分1/x，增加三角形{(0, 0), (1, 0), (1, 1)}，並減去三角形{(0, 0), (b, 0), (b, 1/b)}。
3. Ernest William Hobson, John Napier and the invention of logarithms, 1614, Cambridge: The University Press, 1914
4. Boyer, Carl B., 14，Section "Jobst Bürgi", A History of Mathematics, New York: John Wiley & Sons, 1991, ISBN 978-0-471-54397-8
5. 選取接近e的底數b，對數表涉及的b^x為單調增函數，定義域為0到1而值域為1到b；選取接近1/e的底數b，對數表涉及的b^x為單調減函數，定義域為0到∞而值域為1到0。
6. 以${\displaystyle 10^{\frac {1}{2^{54}}}}$這個接近1的數為基礎。
7. 博納文圖拉·卡瓦列里在1635年的《Geometria indivisibilibus continuorum nova quadam ratione promota》中給出定積分：

   ${\displaystyle \int _{0}^{a}x^{n}\,dx={\tfrac {1}{n+1}}\,a^{n+1}\qquad n\geq 0,}$

   其不定積分形式為：

   ${\displaystyle \int x^{n}\,dx={\tfrac {1}{n+1}}\,x^{n+1}+C\qquad n\neq -1.}$

   獨立發現者還有：皮埃爾·德·費馬、羅貝瓦爾的吉爾（英語：Gilles de Roberval）和埃萬傑利斯塔·托里拆利。
8. 設a=1，x軸上[a,b]兩點對應的雙曲線線段與原點圍成的雙曲線扇形面積為f(b)，[c,d]對應的扇形面積為f(d)-f(c)，d=bc，即為f(bc)-f(c)，當且僅當f(bc)=f(b)+f(c)時，兩雙曲線扇形面積相等。
9. J. J. O'Connor; E. F. Robertson, The number e, The MacTutor History of Mathematics archive, September 2001 [2009-02-02], （原始內容存檔於2012-02-19）
10. 卡瓦列里弓形面積公式，對於負數值的n(x的負數冪)，由於在x = 0處有個奇異點，因此定積分的下限為1，而不是0，即為：

    ${\displaystyle \int _{1}^{a}x^{n}\,dx={\tfrac {1}{n+1}}(a^{n+1}-1)\qquad n\neq -1.}$

    歐拉的自然對數定義：

    ${\displaystyle {\begin{aligned}\ln(x)&=\lim _{n\rightarrow \infty }n(x^{1/n}-1)\\&=\lim _{n\rightarrow -1}{\tfrac {1}{n+1}}(x^{n+1}-1)\\\end{aligned}}}$

11. Maor, Eli, e: The Story of a Number, Princeton University Press, 2009, ISBN 978-0-691-14134-3,sections 1, 1.
    Eves, Howard Whitley, An introduction to the history of mathematics, The Saunders series 6th, Philadelphia: Saunders, 1992, ISBN 978-0-03-029558-4, section 9-3
    Boyer, Carl B., A History of Mathematics, New York: John Wiley & Sons, 1991, ISBN 978-0-471-54397-8, p. 484, 489
12. ${\displaystyle \left(1+{\frac {1}{n}}\right)^{x}=\left(\left(1+{\frac {1}{n}}\right)^{n}\right)^{\frac {x}{n}}}$
    在最初的概念下，底數是接近1的數，而對數是整數；經過簡單變換後，底數變大了，成為接近數學常數e的數，而對數變小了，成為 x/n。
13. Lang 1997, section IV.2
14. Wolfram, Stephen. "Calculation of d/dx(Log(b,x))". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research. （原始內容存檔於2011-07-18） （英語）.
15. Kline, Morris, Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications, 1998, ISBN 978-0-486-40453-0, p. 386
16. Havil, Julian, Gamma: Exploring Euler's Constant, Princeton University Press, 2003, ISBN 978-0-691-09983-5, sections 11.5 and 13.8
17. Eves, Howard, Foundations and Fundamental Concepts of Mathematics, Courier Dover Publications: 59, 2012, ISBN 9780486132204, We also owe to Lambert the first systematic development of the theory of hyperbolic functions and, indeed, our present notation for these functions.
18. Ratcliffe, John, Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics 149, Springer: 99, 2006 [2014-03-28], ISBN 9780387331973, （原始內容存檔於2014-01-12）, That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786.
19. Sarason, Section IV.9.

延伸閱讀

• John B. Conway, Functions of one complex variable, 2nd edition, Springer, 1978.
• Serge Lang, Complex analysis, 3rd edition, Springer-Verlag, 1993.
• Gino Moretti, Functions of a Complex Variable, Prentice-Hall, Inc., 1964.
• Donald Sarason, Complex function theory （頁面存檔備份，存於互聯網檔案館）, 2nd edition, American Mathematical Society, 2007.
• E. T. Whittaker（英語：E. T. Whittaker） and G. N. Watson, A Course in Modern Analysis, fourth edition, Cambridge University Press, 1927.