拱點

拱點（來自古希臘語 ἁψίς (hapsís)，意即：「arch, vault」; pl. apsides /ˈæpsɪˌdiːz/ AP-sih-deez）^[1][2]是行星體在圍繞其主體的橢圓軌道中，距離主體極端值的兩個點。

拱點是指軌道上的行星體（2和3）相對於主天體（1）到達的最遠（2）和最近（3）點。

例如，對於圍繞太陽的軌道，最遠和最近的極端點被稱為「遠日點」（英語：aphelion）和「近日點」（英語：perihelion）。月球環繞地球公轉軌道的兩個拱點，分別是「遠地點」（英語：apogee）和「近地點」（英語：perigee）。地球環繞太陽公轉軌道的兩個拱點，離太陽最遠和最近的兩個極端點，就是前述的「遠日點」和「近日點」。這兩個術語，「遠日點」和「近日點」，同樣適用於木星和其它的行星，以及彗星、小行星和太陽系內所有繞太陽公轉的天體。

概述

二體系統相互作用的橢圓軌道：較小的衛星體（藍色）繞主體（黃色）運行；兩者都在圍繞它們的共同質心或重心（紅+）的橢圓軌道上
∗近拱點和遠拱點表示距離：軌道飛行器和其宿主之間的最小和最大距離。

在任何的橢圓軌道中都有兩個拱點。每個拱點的名稱在英文都是由詞頭「ap-」、「apo-」創建的（來自 ἀπ(ό), (ap(o)-)，意即：「遠離」）表示最遠的點，或「peri-」（來自 περί (peri-)，意即：「接近」）表示離主體最近的點。詞尾描述主體，地球的詞尾是「-gee」，所以兩個拱點的名字是「apogee」（遠地點）和「perigee」（近地點）。 對於太陽，詞尾是「-helion」，因此名稱是「aphelion」（遠日點）和「perilion」（近日點）。

根據牛頓運動定律，所有的週期軌道都是橢圓。這兩個天體的重心可能位於較大的天體內，例如地-月系統的重心大約是地球中心到其表面的75%。如果與較大的質量相比，較小的質量可以忽略不計（例如，對於衛星），則軌道參數與較小的質量無關。

當用作詞尾時，也就是「-apsis」，該術語可以指當軌道物體位於拱點時，從主體到軌道物體的兩個距離：1）在「periapsis」（近拱點），或2）在「poapsis」（遠拱點，比較兩個圖形的第二個圖）。拱點線表示連接軌道上最近點和最遠點的線的距離；它還簡單地指繞主體運行的物體的極限範圍（見圖的上圖；與見第三圖）。

在航天動力學，拱點在科技上是指中心體的質心與軌道物體質心之間量測的距離。然而，在太空船的情況下，這些術語通常用於指太空船在中心體表面上方的軌道高度（假設標準參考半徑是恆定的）。

開普勒的軌道根數：點F，軌道物體最近的接近點是軌道的近心點（也稱為近拱點）；點H，軌道物體的最遠點，是軌道的遠心點（也稱為遠拱點）；它們之間的紅線是連結拱點的線。

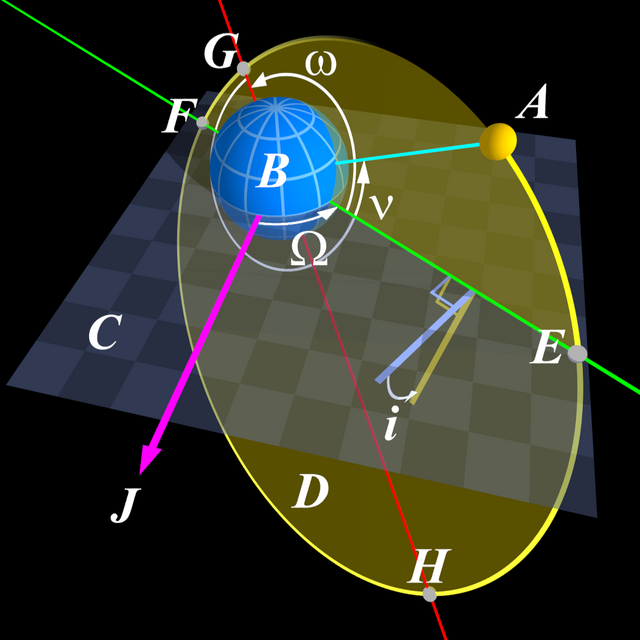
術語

單詞「percenter」（近心點）和「apocenter」（遠心點）經常出現，然而在科技用法上更傾向於使用「periapsis/apoapsis」（近拱點/遠拱點）。

• 對於未指定主軌道的一般情況，術語「近心點」和「遠心點」用於命名軌道上的極值點（見表，上圖）；「近拱點」和「遠拱點」是等效的替代詞。但這些術語也經常只距離，及軌道飛行器和其宿主之間的最小和最大距離periapsis」和「poapsis」（或「papsis」）是等效的替代品，但這些術語也經常指距離，即軌道飛行器與其宿主之間的最小和最大距離（見第二圖）。
• 對於繞太陽運行的天體，距離最小的點是「近日點」（/ˌpɛrɪˈhiːliən/），和距離最大的點是「遠日點」（/æpˈhiːliən/）^[3]。當討論圍繞其它恆星的軌道時，術語變成了「遠星點」和「近星點」。
• 當討論地球的衛星，包括月球時，距離最小的點是「近地點」（perigee，/ˈpɛrɪdʒiː/），並且距離最大的點是「遠地點」（apogee，源自 古希臘語：Γῆ（Gē），"土地"或"土壤"）^[4]。
• 對於月球軌道中的物體，距離最小的點被稱為「近月點」（pericynthion，/ˌpɛrɪˈsɪnθiən/），和距離最大的點稱為「遠月點」（apocynthion，/ˌæpəˈsɪnθiən/）。術語「perilune」和「polune」，以及「perilene」和「poselene」也被使用^[5]。由於月球沒有天然衛星，這只適用於人造物體。

詞源學

「perihelion」（近日點）和「aphelion」（遠日點）這兩個字是約翰尼斯·開普勒鑄造的^[6]，用來描述行星圍繞太陽的軌道運動。這些單詞由詞首「peri-」（希臘語：περί，近）和「apo-」（希臘文：ἀπό，遠離），附在希臘語中表示太陽的單詞上，（ἥλιος，或hēlíos）^[3]。

各種相關術語用於其他天體。詞尾-gee、-helion、-astron和-galacticon，在天文學文獻中經常使用，分別指地球、太陽、恆星和星系中心。詞尾-jove偶爾會使用在木星，但在過去的50年裏，詞尾-saturnium很少使用在土星。-gee的形式也被用作為「任何行星」的術語，是最接近的通用方法，而不是僅適用於地球。

在太陽神計劃期間，「pericynthion」（近月點）和「apocynthion」（遠月點）在提及繞月運行的月球軌道時會使用；他們是參考「Cynthia」（辛西婭，希臘月亮女神阿提米絲的另一個名字。）^[7]。最近，在阿提米斯計劃期間，使用了術語「perilune」和「polune」^[8]。

關於黑洞，術語「peribothron」首先在J.Frank和M.J.Rees 1976年的一篇論文中使用^[9]，他稱讚W·R·斯托格建議用希臘語單詞「bothron」來創造這一個術語。

物理學家和科幻小說作家傑弗里·蘭迪斯在1998年發表的一篇文章中使用了術語「perimelasma」和「apomerasma」（源自希臘詞根）^[10]，因此是在2002年的科學文獻中出現「perinigricon」和「aponigricon」（來自拉丁語）之前^[11]。

術語總結

下面顯示的前綴碼（詞首碼）「peri-」和「apo-」可以添加到字首中，以形成所表示的宿主/母體系統軌道天體的的拱點之唯一名稱。然而，常用這唯一詞首碼的只有地球、月球和太陽系。系外行星研究通常使用「-astron」做為詞尾，而對於其它宿主系統，通常會使用通用詞尾「-apsis」^{[12][與來源不符]}。

太陽系中具有命名/可命名拱點的主體對象

宿主對象	詞尾	名稱來源
太陽	-helion	Helios
水星	-hermion	Hermes
金星	-cythe	Cytherean（英語：Cytherean）
地球	-gee	Gaia
月球	-lune[5] -cynthion -selene[5]	Luna Cynthia Selene
火星	-areion	Ares
穀神星	-demeter[13]	Demeter
木星	-jove	Zeus Jupiter
土星	-chron[5] -kronos -saturnium -krone[14]	Cronos Saturn

其它具有命名/可命名apsides的天體

天體 宿主	詞尾	名稱來源
恆星	-astron	stars
星系	-galacticon	Gr: galaxias; galaxy
質心	-center -focus -apsis
黑洞	-melasma -bothron -nigricon	Gr: melos; black Gr: bothros（英語：bothros）; hole Lat: niger; black

天體	近拱點	遠拱點
銀河系	近銀心點 Perigalacticon	遠銀心點 Apogalacticon
恆星	近星點 Periastron	遠星點 Apastron
黑洞	近黑點 Perimelasma/Peribothra/Perinigricon	遠黑點 Apomelasma/Apobothra/Aponigricon
太陽	近日點 Perihelion	遠日點 Aphelion [15]
水星	近水點 Perihermion	遠水點 Apohermion
金星	近金點 Pericytherion/Pericytherean/Perikrition	遠金點 Apocytherion/Apocytherean/Apokrition
地球	近地點 perigee	遠地點 Apogee
月球	近月點 Periselene/Pericynthion/Perilune	遠月點 Aposelene/Apocynthion/Apolune
火星	近火點 Periareion/Perimartian	遠火點 Apoareion/Apomartian
木星	近木點 Perizene/Perijove	遠木點 Apozene/Apojove
土星	近土點 Perikrone/Perisaturnium	遠土點 Apokrone/Aposaturnium
天王星	近天點 Periuranion	遠天點 Apouranion
海王星	近海點 Periposeidion	遠海點 Apoposedion
冥王星	近冥點 Perihadion	遠冥點 Apohadion

近日點和遠日點

直接圍繞太陽的天體軌道及其最近點（近日點）和最遠點（遠日點）的示意圖。

近日點（q）和遠日點（q）分別是直接圍繞太陽的天體軌道的最近點和最遠點。

將特定曆元的吻切元素與不同時期的元素進行有效比較將產生差異。作為六個吻切元素之一的近日點通過時間不是使用全動力學模型對到太陽的實際最小距離的精確預測（除了通用二體模型）。對近日點通過的精確預測需要數值積分。

內行星和外行星

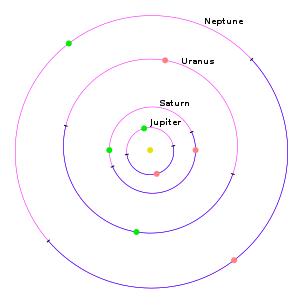
下面的兩張圖顯示了太陽系行星的軌道，軌道交點，以及近日點（q）和遠日點（Q）的位置 ^[16]，如同從地球黃道面的北極上方看到的，它與地球軌道面共面。行星繞太陽逆時針運行，對於每顆行星，其軌道的藍色部分在黃道面以北運行，粉紅色部分在南面運行，圓點標記近日點（綠色）和遠日點（橙色）。

第一張圖片（左下）展示了位於太陽外側的「內部」行星，包括水星、金星、地球和火星。「參考」的地球軌道是黃色的，代表軌道參考平面。春分時，地球在圖的底部。第二張圖片（右下）顯示了「外部」行星，即木星、土星、天王星和海王星。

軌道交點是「交點線」的兩個端點：行星的傾斜軌道與參考平面相交^[17]；在這裏，它們可能被「視為」軌道的藍色部分與粉紅色部分相遇的點。

• 
  太陽系內行星的近日點（綠色）和遠日點（橙色）。
• 
  太陽系外行星的近日點（綠色）和遠日點（橙色）。

拱線

該圖表顯示了太陽系的幾個天體軌道的極端範圍——從最近點（近日點）到最遠點（遠日點）：行星，已知的矮行星，包括穀神星和哈雷彗星。 水平條的長度對應於所指示天體圍繞太陽的軌道極端範圍。這些極端距離（近日點和遠日點之間）是宿主周圍各種物體軌道的「拱線」。

太陽系中所選擇的天體與太陽的距離。每個條形的左右邊緣分別對應於天體近日點和遠日點，長條表示高的軌道離心率。太陽的半徑約70萬公里，木星（最大的行星）約7萬公里，都太小，在這個圖像中顯示不出來。

更近的視角

將距離縮小到只有八大行星與哈雷彗星的範圍：

若將視野縮得更小，只限於內行星的範圍：

地球的近日點和遠日點

現時，地球在1月初到達近日點，大約在12月至日後14天。在近日點，地球的中心與太陽中心的距離大約是6999983290000000000♠0.98329天文單位（AU）或147,098,070 km（91,402,500 mi）。相較之下，地球現時在7月初到達遠日點，大約在六月至日後14天。地球和太陽中心之間的遠日點距離現時約為7011152097651119397♠1.01671 AU或152,097,700 km（94,509,100 mi）.

近日點和遠日點的日期隨着時間的推移而變化，這是由於歲差和其他軌道因素，這些因素遵循被稱為米蘭科維奇循環的週期性模式。在短期內，這些日期可能因年份而異，最多可以有2天的變化^[18]。這種顯著的變化是由於月球的存在：當地月質心在圍繞太陽的穩定軌道上移動時，地球中心的位置與質心的平均距離約為4,700公里（2,900英里），並可能移動在質心的任何方向——這會影響太陽和地球中心之間實際最接近的時間（這反過來又定義了給定年份中近日點的時間）^[19]。

由於遠日點距離的增加，使得落在地球表面給定區域的太陽輻射量只有近日點的93.55%，但這並不能解釋季節，與地球軌道垂直平面的23.4°地軸傾斜，才是季節的成因^[20]。事實上，在近日點和遠日點，地球在一個半球是夏天，而在另一個半球則是冬天。無論地球與太陽的距離如何，冬天落在陽光傾斜照射的半球，夏天落在陽光能垂直照射的半球。

在北半球，此時太陽輻射量最低，夏季與遠日點同時發生。儘管如此，北半球的夏天平均來說比南半球的夏天熱2.3 °C（4 °F）。這是因為北半球有更多的陸地，比海洋更容易加熱^[21]。

然而，近日點和遠日點確實對季節有間接影響：因為地球的軌道速度在遠日點是最小的，在近日點是最大的。所以從6月至9月分至點的軌道運行時間比從12月至3月分至點的時間要長。因此，北半球的夏季持續時間（93日）比南半球的夏季持續時間（89日）長^[22]。

天文學家通常不用日和小時來表示相對於春分點的近日點的時間差，而是用軌道位移的角度來表示，即所謂的近心點經度（也稱為近心經度）。在2010年，這一數值已經增加了一些，達到約283.067°^[23]。

對於地球圍繞太陽的軌道，經過遠地點的時間通常用相對於季節的時間來表示，因為這決定了橢圓軌道對季節變化的貢獻。季節的變化主要由太陽仰角的年度週期控制，這是從黃道面測量地軸傾斜的結果。地球的偏心率和其它軌道元素都不是恆定的，會由於太陽系中行星和其它天體的擾動效應而緩慢變化（米蘭科維奇循環）。

在很長的時間尺度上，近日點和遠日點的日期隨着季節的變化而變化，它們在22,000到26,000年內形成一個完整的週期。從地球上看，恆星的位置有着相應的運動，稱為拱線進動。（這與軸向進動密切相關。）下表列出了過去和未來幾年的近日點和遠日點的日期和時間^[24]：

年	近日點		遠日點
	日期	時間（UT）	日期	時間（UT）
2010	1月3日	00:09	7月6日	11:30
2011	1月3日	18:32	7月4日	14:54
2012	1月5日	00:32	7月5日	03:32
2013	1月2日	04:38	7月5日	14:44
2014	1月4日	11:59	7月4日	00:13
2015	1月4日	06:36	7月6日	19:40
2016	1月2日	22:49	7月4日	16:24
2017	1月4日	14:18	7月3日	20:11
2018	1月3日	05:35	7月6日	16:47
2019	1月3日	05:20	7月4日	22:11
2020	1月5日	07:48	7月4日	11:35
2021	1月2日	13:51	July 5	22:27
2022	1月4日	06:55	7月4日	07:11
2023	1月4日	16:17	7月6日	20:07
2024	1月3日	00:39	7月5日	05:06
2025	1月4日	13:28	7月3日	19:55
2026	1月3日	17:16	7月6日	17:31
2027	1月3日	02:33	7月5日	05:06
2028	1月5日	12:28	7月3日	22:18
2029	1月2日	18:13	7月6日	05:12

其它行星

下表顯示了行星和矮行星在近日點和遠日點與太陽的距離^[25]。

天體類型	天體	近日點距離	遠日點距離	差異（%）	太陽輻照度（英語：Solar irradiance） 差異（%）
行星	1 !水星	46,001,009 km（28,583,702 mi）	69,817,445 km（43,382,549 mi）	34%	57%
	2 !金星	107,476,170 km（66,782,600 mi）	108,942,780 km（67,693,910 mi）	1.3%	2.8%
	3 !地球	147,098,291 km（91,402,640 mi）	152,098,233 km（94,509,460 mi）	3.3%	6.5%
	4 !火星	206,655,215 km（128,409,597 mi）	249,232,432 km（154,865,853 mi）	17%	31%
	5 !木星	740,679,835 km（460,237,112 mi）	816,001,807 km（507,040,016 mi）	9.2%	18%
	6 !土星	1,349,823,615 km（838,741,509 mi）	1,503,509,229 km（934,237,322 mi）	10%	19%
	7 !天王星	2,734,998,229 km（1.699449110×109 mi）	3,006,318,143 km（1.868039489×109 mi）	9.0%	17%
	8 !海王星	4,459,753,056 km（2.771162073×109 mi）	4,537,039,826 km（2.819185846×109 mi）	1.7%	3.4%
矮行星	9 !穀神星	380,951,528 km（236,712,305 mi）	446,428,973 km（277,398,103 mi）	15%	27%
	10 !冥王星	4,436,756,954 km（2.756872958×109 mi）	7,376,124,302 km（4.583311152×109 mi）	40%	64%
	11 !姙神星	5,157,623,774 km（3.204798834×109 mi）	7,706,399,149 km（4.788534427×109 mi）	33%	55%
	12 !鳥神星	5,671,928,586 km（3.524373028×109 mi）	7,894,762,625 km（4.905578065×109 mi）	28%	48%
	13 !鬩神星	5,765,732,799 km（3.582660263×109 mi）	14,594,512,904 km（9.068609883×109 mi）	60%	84%

公式

描繪軌道的近拱點和遠拱點的公式如下：

• 近拱點：在最短的距離處有最快的速度

${\displaystyle v_{\mathrm {per} }={\sqrt {\frac {(1+e)\mu }{(1-e)a}}}\,}$

${\displaystyle r_{\mathrm {per} }=(1-e)a\!\,}$

• 遠拱點：在最遠的距離上有最慢的速度

${\displaystyle v_{\mathrm {ap} }={\sqrt {\frac {(1-e)\mu }{(1+e)a}}}\,}$

${\displaystyle r_{\mathrm {ap} }=(1+e)a\!\,}$

此處，它符合開普勒行星運動定律（角動量守恆）和能量守恆，在一條給定的軌道上測量都是定值：

• 比較相對角動量 ${\displaystyle h={\sqrt {(1-e^{2})\mu a}}}$
• 比較軌道能量 ${\displaystyle \epsilon =-{\frac {\mu }{2a}}}$

此處：

• ${\displaystyle a\!\,}$ 指半主軸(semi-major axis)。
• ${\displaystyle h\!\,}$ 指比較相對角動量(specific relative angular momentum)。
• ${\displaystyle \epsilon \!\,}$ 指比較軌道能量(specific orbital energy)。
• ${\displaystyle \mu \!\,}$ 指標準重力參數值(standard gravitational parameter)。
• ${\displaystyle e\!\,}$ 指軌道離心率，定義為：

${\displaystyle e={\frac {r_{\mathrm {ap} }-r_{\mathrm {per} }}{r_{\mathrm {ap} }+r_{\mathrm {per} }}}=1-{\frac {2}{{\frac {r_{\mathrm {ap} }}{r_{\mathrm {per} }}}+1}}}$

相關條目

• 偏近點角（Eccentric anomaly）
• 橢圓軌道
• 近地點
• 拱點進動（英語：Apsidal precession）

註解和參考資料

1. Template:Cite Dictionary.com
2. apsis. The American Heritage Dictionary of the English Language 5th. Boston: Houghton Mifflin Harcourt.
3. ，自從太陽，「在希臘，λιος以母音開頭（在希臘，H是長ē母音），詞首中省略了「apo」中的最後一個o。=許多詞典都給出了「Ap helion」的發音 [1] 互聯網檔案館的存檔，存檔日期December 22, 2015，.，用不同的音節發音「p」和「h」。然而，發音/əˈfiːliən/ [2] 互聯網檔案館的存檔，存檔日期July 29, 2017，.也是常見的（e.g., McGraw Hill Dictionary of Scientific and Technical Terms, 5th edition, 1994, p. 114），因為在希臘語晚期，「p」來自 ἀ πξ後接「h」ἥ λις變為φ；因此，希臘語單詞是αφήλιον（參見，例如Walker，John，「希臘語、拉丁語和聖經專有名詞的經典發音的關鍵」，Townsend Young [3] 互聯網檔案館的存檔，存檔日期September 21, 2019，.，page 26.）許多 [4] （頁面存檔備份，存於互聯網檔案館）字典給出兩種發音
4.  Chisholm, Hugh (編). Perigee. Encyclopædia Britannica 21 (第11版). London: Cambridge University Press: 149. 1911.
5. Basics of Space Flight. NASA. [May 30, 2017]. （原始內容存檔於September 30, 2019）.
6. Klein, Ernest, A Comprehensive Etymological Dictionary of the English Language, Elsevier, Amsterdam, 1965. (Archived version)
7. Apollo 15 Mission Report. Glossary. [October 16, 2009]. （原始內容存檔於March 19, 2010）.
8. R. Dendy; D. Zeleznikar; M. Zemba. NASA Lunar Exploration – Gateway's Power and Propulsion Element Communications Links. 38th International Communications Satellite Systems Conference (ICSSC). Arlington, VA. September 27, 2021 [July 18, 2022]. （原始內容存檔於Mar 29, 2022）.
9. Frank, J.; Rees, M.J. Effects of massive black holes on dense stellar systems.. MNRAS. September 1, 1976, 176 (6908): 633–646. Bibcode:1976MNRAS.176..633F. doi:10.1093/mnras/176.3.633 .
10. Perimelasma 互聯網檔案館的存檔，存檔日期February 25, 2019，., by Geoffrey Landis, first published in Asimov's Science Fiction, January 1998, republished at Infinity Plus
11. R. Schödel; T. Ott; R. Genzel; R. Hofmann; M. Lehnert; A. Eckart; N. Mouawad; T. Alexander; M. J. Reid; R. Lenzen; M. Hartung; F. Lacombe; D. Rouan; E. Gendron; G. Rousset; A.-M. Lagrange; W. Brandner; N. Ageorges; C. Lidman; A. F. M. Moorwood; J. Spyromilio; N. Hubin; K. M. Menten. A star in a 15.2-year orbit around the supermassive black hole at the centre of the Milky Way. Nature. October 17, 2002, 419 (6908): 694–696. Bibcode:2002Natur.419..694S. PMID 12384690. S2CID 4302128. arXiv:astro-ph/0210426 . doi:10.1038/nature01121.
12. MAVEN » Science Orbit. [November 7, 2018]. （原始內容存檔於November 8, 2018）.
13. Dawn Journal: 11 Years in Space. www.planetary.org. [October 24, 2018]. （原始內容存檔於October 24, 2018）.
14. Cecconi, B.; Lamy, L.; Zarka, P.; Prangé, R.; Kurth, W. S.; Louarn, P. Goniopolarimetric study of the revolution 29 perikrone using the Cassini Radio and Plasma Wave Science instrument high-frequency radio receiver. Journal of Geophysical Research: Space Physics. March 4, 2009, 114 (A3): A03215 [December 9, 2019]. Bibcode:2009JGRA..114.3215C. doi:10.1029/2008JA013830. （原始內容存檔於December 9, 2019） –透過ui.adsabs.harvard.edu.
15. Properly pronounced 'affelion' because the (neo) Greek is αφήλιον, although the hypercorrection 'ap-helion' is commonly heard.
16. the definition of apsis. Dictionary.com. [November 28, 2015]. （原始內容存檔於December 8, 2015）.
17. Darling, David. line of nodes. The Encyclopedia of Astrobiology, Astronomy, and Spaceflight. [May 17, 2007]. （原始內容存檔於August 23, 2019）.
18. Perihelion, Aphelion and the Solstices. timeanddate.com. [January 10, 2018]. （原始內容存檔於January 3, 2018）.
19. Variation in Times of Perihelion and Aphelion. Astronomical Applications Department of the U.S. Naval Observatory. August 11, 2011 [January 10, 2018]. （原始內容存檔於January 11, 2018）.
20. Solar System Exploration: Science & Technology: Science Features: Weather, Weather, Everywhere?. NASA. [September 19, 2015]. （原始內容存檔於September 29, 2015）.
21. Earth at Aphelion. Space Weather. July 2008 [July 7, 2015]. （原始內容存檔於July 17, 2015）.
22. Rockport, Steve C. How much does aphelion affect our weather? We're at aphelion in the summer. Would our summers be warmer if we were at perihelion, instead?. Planetarium. University of Southern Maine. [4 July 2020]. （原始內容存檔於July 6, 2020）.
23. Data.GISS: Earth's Orbital Parameters. data.giss.nasa.gov. （原始內容存檔於2015-10-02）.
24. Espenak, Fred. Earth at Perihelion and Aphelion: 2001 to 2100. astropixels. [June 24, 2021]. （原始內容存檔於July 13, 2021）.
25. NASA planetary comparison chart. [August 4, 2016]. （原始內容存檔於August 4, 2016）.

外部連結

• Apogee - Perigee （頁面存檔備份，存於互聯網檔案館） Photographic Size Comparison
• Aphelion - Perihelion （頁面存檔備份，存於互聯網檔案館） Photographic Size Comparison
• Aphelion - Perihelion Dates and Times （頁面存檔備份，存於互聯網檔案館）