雙縫實驗中光子的動力學

雙縫實驗中光子的動力學描述了在雙縫實驗中，經典電磁波和其量子化的對應物——光子之間的關係。表面上，只要將經典場解釋為光子的機率幅，光子的動力學似乎就能用經典的麥克斯韋方程組完全描述。然而，這種解釋充滿疏漏，並最終會導致矛盾的結論。也就是說，我們不能將電磁場看作是光子的波函數。主要原因在於，電磁場是物理實在的並且是可觀測的；而從原理上說（即不管使用什麼儀器），滿足薛定諤方程式的波函數都不是可觀測量。從而，電磁場是一種物理實在的可觀測場，而不僅僅代表了對振幅取模平方所對應的在某處找到光子的機率。而光子的波函數是否可定義，仍然是一個懸而未決的問題^[1]。

雙縫實驗的經典描述

電磁波方程式

主條目：電磁波方程式

參見：非齊次的電磁波方程式

電磁波方程式^[2]是一種簡化了的麥克斯韋方程組，它描述了電磁場在真空或介質中的傳播。電磁波方程式的齊次形式，以電場${\displaystyle \mathbf {E} \,}$或磁場${\displaystyle \mathbf {B} \,}$的形式寫成

${\displaystyle \nabla ^{2}\mathbf {E} \ -\ {1 \over c^{2}}{\partial ^{2}\mathbf {E} \over \partial t^{2}}\ \ =\ \ 0}$

${\displaystyle \nabla ^{2}\mathbf {B} \ -\ {1 \over c^{2}}{\partial ^{2}\mathbf {B} \over \partial t^{2}}\ \ =\ \ 0}$

其中${\displaystyle c\,}$是真空或介質中的光速。對於真空，c = 2.998 x 10⁸米/秒，也就是光在自由空間中的速度。

磁場和電場之間的聯繫由麥克斯韋修正的安培定律給出：

${\displaystyle \nabla \times \mathbf {B} ={1 \over c}{\frac {\partial \mathbf {E} }{\partial t}}}$.

電磁波方程式的平面波解

主條目：電磁波方程式的正弦平面波解

沿z方向傳播的電磁波可由一個平面正弦波來給出（在厘米-克-秒制和國際單位制下）：

${\displaystyle \mathbf {E} (\mathbf {z} ,t)={\begin{pmatrix}E_{x}^{0}\cos \left(kz-\omega t+\alpha _{x}\right)\\E_{y}^{0}\cos \left(kz-\omega t+\alpha _{y}\right)\\0\end{pmatrix}}=E_{x}^{0}\cos \left(kz-\omega t+\alpha _{x}\right){\hat {\mathbf {x} }}\;+\;E_{y}^{0}\cos \left(kz-\omega t+\alpha _{y}\right){\hat {\mathbf {y} }}}$

以上為電向量。

${\displaystyle \mathbf {B} (\mathbf {z} ,t)={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {z} ,t)={\begin{pmatrix}-E_{y}^{0}\cos \left(kz-\omega t+\alpha _{x}\right)\\E_{x}^{0}\cos \left(kz-\omega t+\alpha _{y}\right)\\0\end{pmatrix}}=-E_{y}^{0}\cos \left(kz-\omega t+\alpha _{y}\right){\hat {\mathbf {x} }}\;+\;E_{x}^{0}\cos \left(kz-\omega t+\alpha _{x}\right){\hat {\mathbf {y} }}}$

以上為磁向量，其中${\displaystyle k\,}$是波數。

${\displaystyle \omega _{}^{}=ck}$

是波的角頻率。向量正上方的標記分別表示x、y和z方向的單位向量。

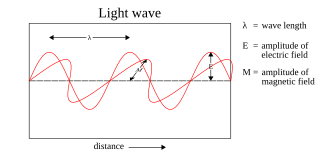電磁輻射是橫向振動的同相電場和磁場的傳播。這一示意圖表示了一個線偏振的平面電磁波從左向右的傳播。

其中的參數包括振幅

${\displaystyle E_{x}^{0}=\mid \mathbf {E} \mid \cos \theta }$

${\displaystyle E_{y}^{0}=\mid \mathbf {E} \mid \sin \theta }$

和相位

${\displaystyle \alpha _{x}^{},\alpha _{y}}$

其中

${\displaystyle \theta \ {\stackrel {\mathrm {def} }{=}}\ \tan ^{-1}\left({E_{y}^{0} \over E_{x}^{0}}\right)}$.

${\displaystyle \mid \mathbf {E} \mid ^{2}\ {\stackrel {\mathrm {def} }{=}}\ \left(E_{x}^{0}\right)^{2}+\left(E_{y}^{0}\right)^{2}}$.

這個解可被寫為簡潔的形式

${\displaystyle \mathbf {E} (\mathbf {z} ,t)=\mid \mathbf {E} \mid \mathrm {Re} \left\{|\psi \rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}}$

其中

${\displaystyle |\psi \rangle \ {\stackrel {\mathrm {def} }{=}}\ {\begin{pmatrix}\psi _{x}\\\psi _{y}\end{pmatrix}}={\begin{pmatrix}\cos \theta \exp \left(i\alpha _{x}\right)\\\sin \theta \exp \left(i\alpha _{y}\right)\end{pmatrix}}}$

是x-y平面的瓊斯向量。這裏這個向量的記法是借用了量子力學中的狄拉克符號。之所以用狄拉克符號來標註瓊斯向量是希望將其理解為量子力學中的態向量。

電磁波方程式的球面波和柱面波解

球面波

從一個源點發出的球面波解為

${\displaystyle \mathbf {E} (\mathbf {r} ,t)=\mid \mathbf {E} (\mathbf {r_{0}} ,t)\mid \left({r_{0} \over r}\right)\mathrm {Re} \left\{|\psi \rangle \exp \left[i\left(kr-\omega t\right)\right]\right\}}$

其中${\displaystyle r\,}$是從波源出發的距離，而${\displaystyle r_{0}\,}$是對應電場強度 ${\displaystyle \mathbf {E} (\mathbf {r_{0}} ,t)}$的從波源出發的距離。

而磁場和電場的關係為

${\displaystyle \mathbf {B} (\mathbf {r} ,t)={\hat {\mathbf {r} }}\times \mathbf {E} (\mathbf {r} ,t)}$

其中單位向量是沿徑向的。

柱面波

從一根無限長波源線發出的柱面波解是貝索函數。對於遠源情形，解簡化為如下形式：

${\displaystyle \mathbf {E} (\mathbf {r} ,t)=\mid \mathbf {E} (\mathbf {r_{0}} ,t)\mid \left({r_{0} \over r}\right)^{1/2}\mathrm {Re} \left\{|\psi \rangle \exp \left[i\left(kr-\omega t\right)\right]\right\}}$

${\displaystyle \mathbf {B} (\mathbf {r} ,t)={\hat {\mathbf {r} }}\times \mathbf {E} (\mathbf {r} ,t)}$

其中${\displaystyle r\,}$和${\displaystyle r_{0}\,}$的意義同上，和球面波呈${\displaystyle {\frac {1}{r}}\,}$衰減相比，柱面波的衰減為${\displaystyle {\frac {1}{\sqrt {r}}}\,}$。

惠更斯原理

主條目：惠更斯－菲涅耳原理

惠更斯原理所描述的波的繞射

惠更斯原理指出，向前行進的波前上的每一點都實則為新的擾動中心，從而成為新的子波源；而波前本身是所有這些子波疊加形成的包絡。

這個原理意味着一束平面波傳播至一個屏障上兩個相鄰的狹縫時，這兩個狹縫可視作相關的波源。如果狹縫本身的長度和觀察者所在距離相比很長，則觀察到的波是柱面波；反之則是球面波。對於任意一種情形，從狹縫發出的電場正比於

${\displaystyle \mathrm {Re} \left\{|\psi \rangle \exp \left[i\left(kr-\omega t\right)\right]\right\}\ {\stackrel {\mathrm {def} }{=}}\ \mathrm {Re} \left\{|\phi \rangle \right\}}$.

干涉

主條目：干涉 (物理學)

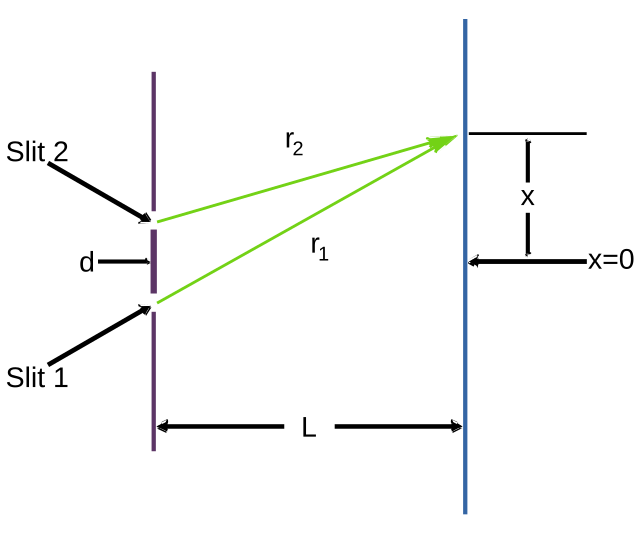雙縫實驗

考慮兩個相鄰距離為d的狹縫，在離狹縫距離為L處放置一個屏，則從狹縫1到屏上一點x的距離為

${\displaystyle r_{1}={\sqrt {L^{2}+x^{2}}}}$

從狹縫2到屏上同一點x的距離為

${\displaystyle r_{2}={\sqrt {L^{2}+(x-d)^{2}}}}$.

當L很大，而x和L相比很小時，兩者的距離差近似等於

${\displaystyle \Delta r\approx {xd \over r_{1}}\approx {xd \over L}}$.

場點x處的電場是來自每個狹縫的波前的疊加並正比於下面相位的實部：

${\displaystyle |\phi _{1}\rangle +|\phi _{2}\rangle =|\psi \rangle \left\{\exp \left[i\left(kr_{1}-\omega t\right)\right]+\exp \left[i\left(kr_{2}-\omega t\right)\right]\right\}=|\phi _{1}\rangle \exp \left[i\left(k\Delta r-\omega t\right)\right].}$

托馬斯·楊描繪雙縫實驗的草圖

入射到場點x的電磁波的總能量正比於電場的模平方，從而正比於

${\displaystyle \cos ^{2}\left(k\Delta r\right)\approx \cos ^{2}\left(2\pi {xd \over \lambda }\right)}$

其中${\displaystyle \lambda \,}$是電磁波的波長。當相位是${\displaystyle \pi \,}$的整數倍時來自狹縫的兩列波有建設性干涉，形成干涉駐波的波腹：

${\displaystyle 2\pi {xd \over \lambda }=n\pi \quad n=0,1,2,\cdots }$

即

${\displaystyle x_{n}={n\lambda \over 2d}\quad n=0,1,2,\cdots }$.

而在相位是${\displaystyle \pi /2\,}$的奇數倍時有破壞性干涉，此時對應着干涉駐波中兩個相鄰波腹當中的波節。

雙縫實驗的量子描述

主條目：光子

以上的處理方法都是經典的。不過，這種方法可以被推廣成量子力學的方法，只需要將其中一個經典量重新解釋為量子力學量。這個量就是上面用狄拉克符號寫成的瓊斯向量${\displaystyle \mid \phi \rangle }$：將其從原本雙縫實驗中的經典描述改為用於描述光子量子態的態向量。

光子的能量和動量

通過普朗克的能量量子化假設和愛因斯坦對光電效應實驗的解釋，愛因斯坦提出了電磁波的能量是由不可再分的能量子組成的，這種不可再分的能量子稱為光子。

能量

由普朗克的能量量子化假設，光子的能量正比於電磁波的角頻率：

${\displaystyle \epsilon =\hbar \omega }$

則如在體積為V的盒子內存在有N個光子，電磁場的能量密度為${\displaystyle {N\hbar \omega \over V}}$。

根據對應原理，當光子數量很大時，量子化的能量密度必須和經典場的能量密度一致。從而對於很大的N，我們有

${\displaystyle {N\hbar \omega \over V}={\mathcal {E}}_{c}={\frac {\mid \mathbf {E} \mid ^{2}}{8\pi }}}$.

則可得到盒子中的光子數量

${\displaystyle N={\frac {V}{8\pi \hbar \omega }}\mid \mathbf {E} \mid ^{2}}$.

動量

用電子進行的雙縫實驗，用光子得到的結果也類似於此。本圖描述的是隨時間的累積，到達屏幕的電子的分佈情況。^{[註 1]}

從對應原理還可以得到光子的動量，其動量密度對應着經典的玻印亭向量除以光速的平方，即

${\displaystyle {\mathcal {P}}_{c}={N\hbar \omega \over cV}={N\hbar k \over V}}$

即一個光子的動量為${\displaystyle \hbar k}$。

量子力學中的機率本性

單個光子的干涉

將機率的概念應用到解釋光子的行為時，有兩種方法可以考慮：一種是用機率計算處在某個特定態上的可能的光子數量，另一種是用機率計算單個光子處在某個特定態上的可能性。前一種方法的結果會違反能量守恆；後一種方法雖然不直觀但確實是可行的。狄拉克在雙縫實驗中對這一點進行了解釋^[4]：

“	在量子力學發現以前不久，人們就已了解到，光波和光子之間的聯繫必須是統計的性質。然而，他們沒有清楚地了解到，波函數告訴我們的是一個光子在一特定位置上的機率，而不是在那個位置上可能有的光子數目。這一區別的重要性可在下面看清楚。假定我們令大量光子組成的光束分裂為兩個強度相等的部分。按照光束的強度與其中可能的光子數目相聯繫的假定，我們就會得到，光子總數的一半分別走入每一組分。現在，如果使這兩個組分互相干涉，我們就得要求，在一個組分中的一個光子能夠與另一組分中的一個光子互相干涉。在某些情況下，這兩個光子就要互相抵消，而在另一些情況下，它們就要產生四個光子。這樣一來，就會和能量守恆相矛盾了。而新的理論把波函數與一個光子的機率聯繫起來，就克服了這一困難，因為這個理論認定，每一光子都是部分地走入兩個組分中的每一個。這樣，每一個光子只與它自己發生干涉。從來不會出現兩個不同的光子之間的干涉。	”
——保羅·狄拉克，《量子力學原理》第四版，第一章第3節

機率幅

光子處於某一偏振態的機率取決於用麥克斯韋方程組描述的經典場；類似地，一個單光子的福柯態所對應的機率密度和其對應電磁場的能量密度的期望值有關。一般而言，量子力學中機率幅的疊加法則和經典的機率疊加看上去非常相似^[5]：

1. 兩個先後過程的機率疊加得到的機率幅是每一個單獨機率幅的乘積。
2. 一個過程可由多種不可區分的方法之一來完成，則它的機率幅是每一種獨立方法的機率幅的和。
3. 過程發生的總機率是通過第1條和第2條所給出的機率幅的模平方。

參見

• 薛定諤方程式的理論和實驗驗證
• 斯特恩-革拉赫實驗
• 波粒二象性
• 光子的偏振
• 光電效應
• 基爾霍夫繞射公式

註釋

1. 雖然每一點表示一個電子抵達探測屏，這事實並不能表現出電子的粒子性，因為探測器是由離散原子組成的，這可以詮釋為電子波與離散原子彼此之間的相互作用。^[3]

參考文獻

1. Bialynicki-Birula, Iwo. Photon wave function. eprint arXiv:quant-ph/0508202. 2005-08 [2010-01-11]. （原始內容存檔於2013-08-31）.
2. Jackson, John D. Classical Electrodynamics (3rd ed.). Wiley. 1998. ISBN 0-471-30932-X.
3. Hobson, Art. There are no particles, there are only fields. American Journal of Physics. 2013, 81 (211) [2014-09-25]. doi:10.1119/1.4789885. （原始內容存檔於2015-02-10）.
4. Dirac, P. A. M. The Principles of Quantum Mechanics, Fourth Edition. Oxford. 1958. ISBN 0-19-851208-2. 中文譯文來自陳咸亨中譯本《量子力學原理》，科學出版社出版
5. Baym, Gordon. Lectures on Quantum Mechanics. W. A. Benjamin. 1969. ISBN 0-8053-0667-6.