高斯積分

提示：此條目的主題不是高斯求積。

高斯積分（英語：Gaussian integral），有時也被稱為概率積分，是高斯函數（e^−x2）在整個實數線上的積分。它得名於德國數學家兼物理學家卡爾·弗里德里希·高斯之姓氏。

${\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}dx={\sqrt {\pi }}}$

f(x) = e^−x2 的圖像，這個函數與 x 軸之間的面積等於 ${\displaystyle \scriptstyle {\sqrt {\pi }}}$。

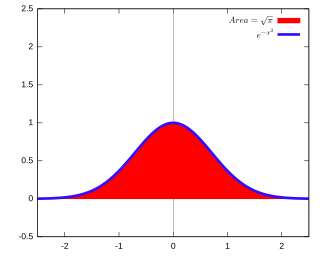
高斯積分用處很廣。例如，利用換元積分法，它可以用來計算正態分布的歸一化常數。在極限為有限值的時候，高斯積分與正態分布的誤差函數和累積分布函數密切相關。在物理學中，這種積分也經常出現：例如在量子力學中，諧振子基態的概率密度；在路徑積分公式中，諧振子的傳播子；以及統計力學中的配分函數，以上的計算都要用到這個積分。

我們可以通過Risch算法證明誤差函數不具有初等函數形式；儘管如此，高斯積分可以通過多元微積分方法分析求解。雖然不定積分${\displaystyle \int e^{-x^{2}}\,dx}$ 無法用初等函數表示，但定積分${\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}\,dx}$是可以計算的。

任意高斯函數的定積分為

${\displaystyle \int _{-\infty }^{\infty }e^{-a(x+b)^{2}}\,dx={\sqrt {\frac {\pi }{a}}}.}$

計算方式

通過極限計算

要想找到高斯積分的閉合形式，首先定義一個近似函數：

${\displaystyle I(a)=\int _{-a}^{a}e^{-x^{2}}dx}$，

高斯積分可以通過它的極限來運算：

${\displaystyle \lim _{a\to \infty }I(a)=\int _{-\infty }^{+\infty }e^{-x^{2}}\,dx.}$

對${\displaystyle I}$取平方獲得

${\displaystyle I^{2}(a)=\left(\int _{-a}^{a}e^{-x^{2}}\,dx\right)\cdot \left(\int _{-a}^{a}e^{-y^{2}}\,dy\right)=\int _{-a}^{a}\left(\int _{-a}^{a}e^{-y^{2}}\,dy\right)\,e^{-x^{2}}\,dx=\int _{-a}^{a}\int _{-a}^{a}e^{-(x^{2}+y^{2})}\,dx\,dy.}$

根據富比尼定理，以上的雙重積分可以被看作是直角坐標系上一個正方形的面積積分${\displaystyle \int e^{-(x^{2}+y^{2})}\,d(x,y)}$，其頂點為${\displaystyle \{(-a,a),(a,a),(a,-a),(-a,-a)\}}$。

不論${\displaystyle x}$為任何實數，指數函數${\displaystyle e^{x}}$均大於0，所以這個正方形的內切圓的積分必須小於${\displaystyle I(a)^{2}}$。同理，正方形的外接圓積分必須大於${\displaystyle I(a)^{2}}$。通過從直角坐標系轉化到極坐標系${\displaystyle x=r\,\cos \theta }$, ${\displaystyle y=r\,\sin \theta }$, ${\displaystyle d(x,y)=r\,d(r,\theta )}$，可以計算出這兩個圓面的積分：

${\displaystyle \int _{0}^{2\pi }\int _{0}^{a}re^{-r^{2}}\,dr\,d\theta <I^{2}(a)<\int _{0}^{2\pi }\int _{0}^{a{\sqrt {2}}}re^{-r^{2}}\,dr\,d\theta }$，

得到

${\displaystyle \pi (1-e^{-a^{2}})<I^{2}(a)<\pi (1-e^{-2a^{2}}).}$

使用夾擠定理獲得高斯積分

${\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}.}$

利用沃利斯積分計算

在這裡，對於n為自然數時，沃利斯積分定義為：

${\displaystyle I_{n}=\int _{0}^{\frac {\pi }{2}}\sin ^{n}x\mathrm {d} x={\begin{cases}{\dfrac {n-1}{n}}\cdot {\dfrac {n-3}{n-2}}\cdots {\dfrac {3}{4}}\cdot {\dfrac {1}{2}}\cdot {\dfrac {\pi }{2}}&2|n\\{\dfrac {n-1}{n}}\cdot {\dfrac {n-3}{n-2}}\cdots {\dfrac {4}{5}}\cdot {\dfrac {2}{3}}\cdot 1&2\nmid n\end{cases}}}$

因此有${\displaystyle {\frac {n+1}{n+2}}={\frac {I_{n+2}}{I_{n}}}}$的關係，並且根據${\displaystyle I_{n+2}\leqslant I_{n+1}\leqslant I_{n}}$以及夾擠定理得到${\displaystyle \lim _{n\to \infty }{\frac {I_{n+1}}{I_{n}}}=1}$，另外也可以得到${\displaystyle {\frac {(n+2)I_{n+1}I_{n+2}}{(n+1)I_{n}I_{n+1}}}=1}$，因此總有${\displaystyle (n+1)I_{n}I_{n+1}=I_{0}I_{1}={\frac {\pi }{2}}}$，於是可以得到：

${\displaystyle {\begin{aligned}\lim _{n\to \infty }{\frac {(n+1)I_{n+1}}{nI_{n}}}&=\lim _{n\to \infty }{\frac {(n+1)I_{n}I_{n+1}}{nI_{n}^{2}}}=\lim _{n\to \infty }{\frac {\pi }{2nI_{n}^{2}}}=1\\\lim _{n\to \infty }{\sqrt {n}}I_{n}&={\sqrt {\frac {\pi }{2}}}\end{aligned}}}$

考慮到${\displaystyle \mathrm {e} ^{t}=\sum _{k=0}^{\infty }{\frac {t^{k}}{k!}}}$以及${\displaystyle {\frac {1}{1-t}}=\sum _{k=0}^{\infty }t^{k}}$，因此當${\displaystyle t\geqslant 0}$時該不等式成立：

${\displaystyle {\frac {1}{1-t}}\geqslant \mathrm {e} ^{t}\geqslant 1+t}$

當${\displaystyle t=x^{2}}$並且不等式各邊取倒數之後，變成：

${\displaystyle 1-x^{2}\leqslant \mathrm {e} ^{-x^{2}}\leqslant {\frac {1}{1+x^{2}}}}$

各邊同時乘方運算與積分，並且最右邊的部分積分區間大於左邊與中間部分，變成：

${\displaystyle \int _{0}^{1}(1-x^{2})^{n}\mathrm {d} x\leqslant \int _{0}^{1}\mathrm {e} ^{-nx^{2}}\mathrm {d} x\leqslant \int _{0}^{\infty }{\frac {\mathrm {d} x}{(1+x^{2})^{n}}}}$

最左邊變量代換為${\displaystyle x=\sin \theta }$得${\displaystyle \mathrm {d} x=\cos \theta \mathrm {d} \theta }$；當中變量代換為${\displaystyle x={\frac {y}{\sqrt {n}}}}$；最右邊變量代換為${\displaystyle x=\tan \theta }$得${\displaystyle \mathrm {d} x=\sec ^{2}\theta \mathrm {d} \theta ={\frac {\mathrm {d} \theta }{\cos ^{2}\theta }}}$，變成：

${\displaystyle \int _{0}^{\frac {\pi }{2}}\cos ^{2n+1}\theta \mathrm {d} \theta \leqslant {\frac {1}{\sqrt {n}}}\int _{0}^{\sqrt {n}}\mathrm {e} ^{-y^{2}}\mathrm {d} y\leqslant \int _{0}^{\frac {\pi }{2}}\cos ^{2n-2}\theta \mathrm {d} \theta }$

利用誘導公式${\displaystyle \cos \left({\frac {\pi }{2}}-\theta \right)=\sin \theta }$，並且同時乘係數${\displaystyle {\sqrt {n}}}$，變成：

${\displaystyle {\sqrt {n}}\int _{0}^{\frac {\pi }{2}}\sin ^{2n+1}\theta \mathrm {d} \theta \leqslant \int _{0}^{\sqrt {n}}\mathrm {e} ^{-y^{2}}\mathrm {d} y\leqslant {\sqrt {n}}\int _{0}^{\frac {\pi }{2}}\sin ^{2n-2}\theta \mathrm {d} \theta }$

此時即為${\displaystyle {\sqrt {n}}I_{2n+1}\leqslant \int _{0}^{\sqrt {n}}\mathrm {e} ^{-y^{2}}\mathrm {d} y\leqslant {\sqrt {n}}I_{2n-2}}$，當${\displaystyle n\to \infty }$時通過夾擠定理可以得到共同極限為${\displaystyle {\frac {\sqrt {\pi }}{2}}}$，最終有${\displaystyle \int _{-\infty }^{\infty }\mathrm {e} ^{-x^{2}}\mathrm {d} x=2\int _{0}^{\infty }\mathrm {e} ^{-x^{2}}\mathrm {d} x={\sqrt {\pi }}}$。

與Γ函數的關係

由於被積分的函數是一個偶函數，

${\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}dx=2\int _{0}^{\infty }e^{-x^{2}}dx}$

通過替代變量它可以變成一個歐拉積分

${\displaystyle \int _{0}^{\infty }e^{-t}\ t^{-{\frac {1}{2}}}dt\,=\,\Gamma \left({\frac {1}{2}}\right)}$

這裡${\displaystyle ~\Gamma }$是Γ函數。這說明了為什麼一個半整數的階乘是${\displaystyle {\sqrt {\pi }}}$的倍數。更廣義地，

${\displaystyle b\int _{0}^{\infty }e^{-ax^{b}}dx=a^{-{\frac {1}{b}}}\,\Gamma \left({\frac {1}{b}}\right).}$

推廣

高斯函數的積分

任一高斯函數的積分都可以用以下的公式計算：

${\displaystyle \int _{-\infty }^{\infty }e^{-a(x+b)^{2}}\,dx={\sqrt {\frac {\pi }{a}}}}$

更為廣泛的形式為：

${\displaystyle \int _{-\infty }^{\infty }e^{-ax^{2}+bx+c}\,dx={\sqrt {\frac {\pi }{a}}}\,e^{{\frac {b^{2}}{4a}}+c}}$

這一公式在計算有關正態分布的一些連續概率分布的數學期望值的時候特別有用，例如對數正態分布。

n維和泛函推廣

主條目：多元正態分布

令${\displaystyle A}$為一個對稱的、正定的（因而可逆）${\displaystyle n\times n}$ 精密矩陣（英語：precision matrix）（即協方差矩陣的逆矩陣），則

${\displaystyle \int _{-\infty }^{\infty }e^{\left(-{\frac {1}{2}}\sum \limits _{i,j=1}^{n}A_{ij}x_{i}x_{j}\right)}\,d^{n}x=\int _{-\infty }^{\infty }e^{\left(-{\frac {1}{2}}x^{T}Ax\right)}\,d^{n}x={\sqrt {\frac {(2\pi )^{n}}{\det A}}}={\sqrt {\frac {1}{\det(A/2\pi )}}}={\sqrt {\det(2\pi A^{-1})}}}$

這裡的積分是對Rⁿ的。上式被用於研究多元正態分布。

同樣，

${\displaystyle \int x^{k_{1}}\cdots x^{k_{2N}}\,e^{\left(-{\frac {1}{2}}\sum \limits _{i,j=1}^{n}A_{ij}x_{i}x_{j}\right)}\,d^{n}x={\sqrt {\frac {(2\pi )^{n}}{\det A}}}\,{\frac {1}{2^{N}N!}}\,\sum _{\sigma \in S_{2N}}(A^{-1})_{k_{\sigma (1)}k_{\sigma (2)}}\cdots (A^{-1})_{k_{\sigma (2N-1)}k_{\sigma (2N)}}}$

這裡的 σ 表示的是有序集 {1, ..., 2N} 的不同排列。等式右邊的係數是對 ${\displaystyle N}$ 個重複的 A^-1 的 {1, ..., 2N} 中所有的組合的求和（the sum over all combinatorial pairings of {1, ..., 2N} of N copies of A⁻¹）。^{[來源請求]}

或者，

${\displaystyle \int f({\vec {x}})e^{\left(-{\frac {1}{2}}\sum \limits _{i,j=1}^{n}A_{ij}x_{i}x_{j}\right)}d^{n}x={\sqrt {(2\pi )^{n} \over \det A}}\,\left.e^{\left({1 \over 2}\sum \limits _{i,j=1}^{n}(A^{-1})_{ij}{\partial \over \partial x_{i}}{\partial \over \partial x_{j}}\right)}f({\vec {x}})\right|_{{\vec {x}}=0}}$

以上積分中的 ${\displaystyle f}$ 是解析函數，且函數值的增長必須滿足某些邊界條件以及另一些特定要求。微分算子的冪可以理解為冪級數。

雖然泛函積分沒有嚴格的定義，但是我們仍然可以依照有限維的情況「定義」高斯泛函積分。^{[來源請求]} 然而，${\displaystyle (2\pi )^{\infty }}$ 無窮大的問題依然存在，且大部分的泛函行列式（英語：Functional determinant）也是無窮大的。如果只考慮比例：

${\displaystyle {\frac {\int f(x_{1})\cdots f(x_{2N})e^{-\iint {\frac {1}{2}}A(x_{2N+1},x_{2N+2})f(x_{2N+1})f(x_{2N+2})d^{d}x_{2N+1}d^{d}x_{2N+2}}{\mathcal {D}}f}{\int e^{-\iint {\frac {1}{2}}A(x_{2N+1},x_{2N+2})f(x_{2N+1})f(x_{2N+2})d^{d}x_{2N+1}d^{d}x_{2N+2}}{\mathcal {D}}f}}={\frac {1}{2^{N}N!}}\sum _{\sigma \in S_{2N}}A^{-1}(x_{\sigma (1)},x_{\sigma (2)})\cdots A^{-1}(x_{\sigma (2N-1)},x_{\sigma (2N)}).}$

則可以解決這個問題。在德維特標記法（英語：DeWitt notation）下，此公式與有限維的情況一致。

帶線性項的n維

如果A是一個對稱的正定矩陣，則有（假設均為列向量）

${\displaystyle \int e^{-{\frac {1}{2}}\sum \limits _{i,j=1}^{n}A_{ij}x_{i}x_{j}+\sum \limits _{i=1}^{n}B_{i}x_{i}}d^{n}x=\int e^{-{\frac {1}{2}}{\vec {x}}^{T}\mathbf {A} {\vec {x}}+{\vec {B}}^{T}{\vec {x}}}d^{n}x={\sqrt {\frac {(2\pi )^{n}}{\det {A}}}}e^{{\frac {1}{2}}{\vec {B}}^{T}\mathbf {A} ^{-1}{\vec {B}}}.}$

形式相似的積分

${\displaystyle \int _{0}^{\infty }x^{2n}e^{-{\frac {x^{2}}{a^{2}}}}\,dx={\sqrt {\pi }}{\frac {a^{2n+1}(2n-1)!!}{2^{n+1}}}}$

${\displaystyle \int _{0}^{\infty }x^{2n+1}e^{-{\frac {x^{2}}{a^{2}}}}\,dx={\frac {n!}{2}}a^{2n+2}}$

${\displaystyle \int _{0}^{\infty }x^{2n}e^{-ax^{2}}\,dx={\frac {(2n-1)!!}{a^{n}2^{n+1}}}{\sqrt {\frac {\pi }{a}}}}$

${\displaystyle \int _{0}^{\infty }x^{2n+1}e^{-ax^{2}}\,dx={\frac {n!}{2a^{n+1}}}}$

${\displaystyle \int _{0}^{\infty }x^{n}e^{-ax^{2}}\,dx={\frac {\Gamma ({\frac {n+1}{2}})}{2a^{\frac {n+1}{2}}}}}$

其中，n 為正整數，「!!」表示雙階乘。 這類積分的一種簡單的計算方式是應用萊布尼茲積分規則（英語：Leibniz integral rule）對參數進行微分：

${\displaystyle {\begin{aligned}\int _{-\infty }^{\infty }x^{2n}e^{-\alpha x^{2}}\,dx&=\left(-1\right)^{n}\int _{-\infty }^{\infty }{\frac {\partial ^{n}}{\partial \alpha ^{n}}}e^{-\alpha x^{2}}\,dx~=\left(-1\right)^{n}{\frac {\partial ^{n}}{\partial \alpha ^{n}}}\int _{-\infty }^{\infty }e^{-\alpha x^{2}}\,dx\\&={\sqrt {\pi }}\left(-1\right)^{n}{\frac {\partial ^{n}}{\partial \alpha ^{n}}}\alpha ^{-{\frac {1}{2}}}~={\sqrt {\frac {\pi }{\alpha }}}{\frac {(2n-1)!!}{\left(2\alpha \right)^{n}}}\end{aligned}}}$

也可以先分部積分，然後找出遞推關係之後求解。

另見

• 高斯函數積分表
• 量子場論中常見的積分（英語：Common integrals in quantum field theory）
• 正態分布
• 指數函數積分表
• 誤差函數
• 格拉斯曼積分（英語：Grassmann integral）

參考資料

• 埃里克·韋斯坦因. Gaussian Integral. MathWorld.
• Griffiths, David. Introduction to Quantum Mechanics 2nd.
• Abramowitz, M.; Stegun, I. A. Handbook of Mathematical Functions. New York: Dover Publications.