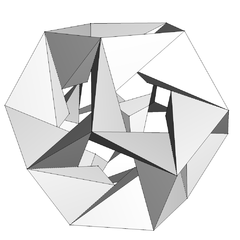
第四星形二十面体是正二十面体的一种星形化体,为正二十面体的面向外延伸并相交所形成的第四种立体,外观看起来像是仅有框架的正十二面体[1]:49,由30个双锥体组成[2]。这个立体最早由哈里·惠勒发现,[3]并认为这个立体是一个离散的结构。[2]
历史
第四星形二十面体最早出现在哈里·惠勒发表于1924年的论文《某些形式的二十面体与特定更高多面体的推导方式》中,惠勒将其描述为形式上离散的多面体[2],并将其编号为22。[3]在1920年至1930年间,米勒定义了一套规则来规范星形二十面体,这个规则能从无限多种星形化多面体中明确定义哪些多面体是“重要且特别”的[4],当中并未排除离散或不连续的结构[5],因此在1938年哈罗德·斯科特·麦克唐纳·考克斯特、帕特里克·杜·瓦尔等人的著作《五十九种二十面体》也收录了这种立体,并编号为11。[6]
构成
第四星形二十面体由30个双三角锥以顶点接顶点的方式,沿著正十二面体的骨架组成。[2]
-
第四星形二十面体
-
正十二面体的骨架图
-
正十二面体
组成这个立体的星形二十面体胞为第10和第12个胞。[7]
 星形二十面体中的胞 |
 第四星形二十面体的胞 |
相关多面体
第十四星形二十面体外观是一个边向某方向扭曲、且有孔洞的空心十二面体,其对称性与凹五角锥十二面体类似。[1]:61这样的结构在polyhedr.com出版的多面体组装模型产品中被评价为“魔术边”(Magic edge)。[8]
第十四星形二十面体在杜瓦记号中记为e1f1g1,不少最外层为g1的星形二十面体皆形如空心二十面体:[6]
| 名称 | 杜瓦记号 | 星状图 | 立体图 |
|---|---|---|---|
| 第四星形二十面体 11 (《五十九种二十面体》) 21(惠勒) |
g1 | 
|

|
| 13 (《五十九种二十面体》) 20(惠勒) |
e1f1g1 | 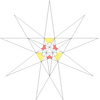
|

|
| 14 (《五十九种二十面体》) | f1g1 | 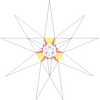 |

|
| 25 (《五十九种二十面体》) | De1f1g1 | 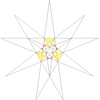 |

|
| 凹五角锥十二面体 26 (《五十九种二十面体》) 9(惠勒) |
Ef1g1 | 
|

|
| 36 (《五十九种二十面体》) | f1g1 | 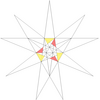 |

|
| 第十四星形二十面体 37 (《五十九种二十面体》) |
e1f1g1 | 
|

|
| 38 (《五十九种二十面体》) | De1f1g1 |  |

|
| 48 (《五十九种二十面体》) | e2f1g1 | 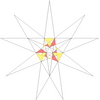 |

|
| 49 (《五十九种二十面体》) | De2f1g1 |  |

|
| 50 (《五十九种二十面体》) | Ef1g1 | 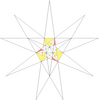 |

|
参见
- 《五十九种二十面体》
参考文献
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.