schlegel diagram

无向图。在图论中，多面体图均为3-连通（英语：k-vertex-connected graph）平面图。 凸多面体的施莱格尔图（英语：Schlegel diagram）将该多面体的边、顶点用线段、端点在二维空间中表示出来，其外观是一个凸多边形里镶套着多个更小的凸多边形。该图的边互相不会交叉，因此多面

構。八面體半形也可看成是一個沒有底面的正四角錐，即正八面體的一半。 八面體半形可以對稱地表示一個六邊形或一個正方形的施萊格爾圖（英语：Schlegel diagram）： 它有著一些特殊的特性：每對頂點之間連接著兩條不同的邊，即每兩個頂點圍成了一個二角形。 立方體半形是正多面體的半形體之一，其他也是正多面體的半形之結構有：

plane） 在透视投影中，如果如果投影中心正在正十二面体外接球正对其一面的一点，则你能得到其施莱格尔图像（英语：schlegel diagram），我们亦可以将其视为球面多面体（英语：Spherical polyhedron）而使用球极投影。这些方法也被用于可视化其四维类比正一

於8個等腰三角形的公共頂點上投影和於3個等腰三角形的公共頂點上投影。 三角化八面體也可以表示為球面鑲嵌，也可以透過施莱格尔投影（英语：Schlegel diagram），於平面上呈現。而其施莱格尔投影的結果在圖論中是一種阿基米德對偶圖，稱為小三角化八面體圖。 三角化八面體出現在部分的藝術創作中，例如

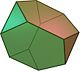
此外，由於截角四面體可以由立方體透過斜截變換構成，即先交錯、再截角，因此，截角四面體又稱為斜截立方體或截角交錯立方體，在考克斯特符號（英语：Coxeter diagram）中計為，頂點數為小斜方截半立方體的一半，因此兩個截角四面體可以構成一個凸包為小斜方截半立方體的截角星形八面體，此種立體也稱為二複合截角四面體。