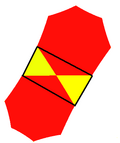
在几何学中，截半正七边形镶嵌（英语：Triheptagonal tiling）是一种由正七边形与正三角形拼合，并且将正七边形重复排列组合，并让图形完全拼合，而且没有空隙或重叠的几何构造。其为正七边形镶嵌经截半变换后的像，是一种双曲半正镶嵌，每个顶点皆由两个正七边形与两个正三角形构成。在施莱夫利符号中用r{7,3}表示；此外其边缘形成一个无限排列的双曲面直线，此性质与截半正六边形镶嵌相似[1][2]。
截半正七边形镶嵌无法在一个平面上构造，因为每个顶点的角度超过了360度，但若硬将正七边形与正三角形边对边接合，将会变成一个马鞍形，且每个顶点皆会落在一个双曲抛物面上，虽然它不能在欧几里得平面上构造，但可以在一个双曲抛物面上构造[3]，因此截半正七边形镶嵌也是罗氏几何或双曲几何中讨论的几何构造。
Remove ads
图片
 克莱因圆盘模型保留了直线，但是扭曲了角度 |
 截半正七边形镶嵌的对偶镶嵌称为七阶三菱形镶嵌（英语：Order-7-3 rhombille tiling），由七个和三个菱形交错的顶点组成。 |
相关半正镶嵌
截半正七边形镶嵌在拓扑上与一系列一直延伸到双曲镶嵌的顶点图为3.n.3.n的（广义）拟正多面体相关：
| 对称性 *n32 [n,3] |
球面 | 欧氏镶嵌 | 紧凑型双曲镶嵌 | 仿紧型镶嵌 | 非紧型镶嵌 | |||
|---|---|---|---|---|---|---|---|---|
| *332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] p6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[iπ/λ,3] | |
| 拟正顶点 布局 |
 3.3.3.3 |
 3.4.3.4 |
 3.5.3.5 |
 3.6.3.6 |
 3.7.3.7 |
 3.8.3.8 |
 3.∞.3.∞ |
 3.∞.3.∞ |
| 考克斯特纪号 |   
|
|
|
|
|
|
|
|
| 对偶 (菱形) 顶点 布局 |
 V3.3.3.3 |
 V3.4.3.4 |
 V3.5.3.5 |
 V3.6.3.6 |
V3.7.3.7 |
 V3.8.3.8 |
 V3.∞.3.∞ |
|
| 考克斯特纪号 | 
|
|
|
|
|
|
|
|
从威佐夫结构中可得到8种不同的半正镶嵌
| 对称群：[7,3], (*732) | [7,3]+, (732) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
| |||
| {7,3} | t{7,3} | r{7,3} | 2t{7,3}=t{3,7} | 2r{7,3}={3,7} | rr{7,3} | tr{7,3} | sr{7,3} | |||
| 半正对偶 | ||||||||||
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| |||
| V73 | V3.14.14 | V3.7.3.7 | V6.6.7 | V37 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | |||
Remove ads
参见
参考文献
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
Remove ads