六角反棱柱

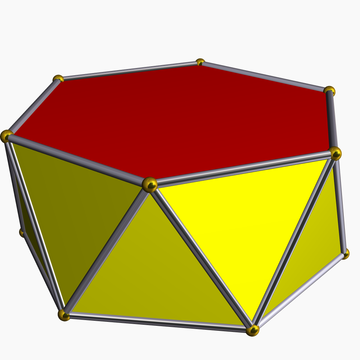
在几何学中，六角反棱柱又称为反六角柱或六角反柱是指底为六边形的反棱柱，侧面由三角形组成，若每一个面皆为正多边形则称为正六角反棱柱。每个六角反棱柱皆含有14个面，是一种十四面体。

正六角反棱柱

类别	反棱柱 柱状均匀多面体
对偶多面体	六方偏方面体
识别
名称	正六角反棱柱
参考索引	U77(d)
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	hap
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）
施莱夫利符号	s{2,6}
威佐夫符号 （英语：Wythoff symbol）	| 2 2 6
康威表示法	A6
性质
面	14
边	24
顶点	12
欧拉特征数	F=14, E=24, V=12 （χ=2）
组成与布局
面的种类	三角形×12 正六边形×2
顶点图	3.3.3.6
对称性
对称群	D6d, [2+,12], (2*6), order 24
旋转对称群 （英语：Rotation_groups）	D6, [6,2]+, (622), order 12
特性
凸
图像
3.3.3.6 （顶点图） 六方偏方面体 （对偶多面体） （展开图）

正六角反棱柱是基底为正六边形的六角反棱柱，其可视为一种半正多面体。

• 
  正六角反棱柱

正六角反棱柱

当一个六角反棱柱的底面为正六边形且侧面为正三角形时，会具备一些特别的性质：

当基底边长为a的时候：

• 顶点数目：12
• 边数目：24
• 面数目：14
• 对偶多面体：六方偏方面体
• 高：${\displaystyle a{\sqrt {{\sqrt {3}}-1}}}$
• 表面积：${\displaystyle 6a^{2}{\sqrt {3}}}$
• 体积：${\displaystyle a^{3}{\sqrt {2(1+{\sqrt {3}}}})}$

相关多面体及镶嵌

半正六边形二面体球面多面体

对称群（英语：List of spherical symmetry groups）：[6,2], (*622)							[6,2]+, (622)	[1+,6,2], (322)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	2t{6,2}=t{2,6}	2r{6,2}={2,6}	rr{6,2}	tr{6,2}	sr{6,2}	h{6,2}	s{2,6}
半正对偶
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V32	V3.3.3.3

半正反棱柱系列

2	3	4	5	6	7	8	9	10	11	12	n
s{2,4} sr{2,2}	s{2,6} sr{2,3}	s{2,8} sr{2,4}	s{2,10} sr{2,5}	s{2,12} sr{2,6}	s{2,14} sr{2,7}	s{2,16} sr{2,8}	s{2,18} sr{2,9}	s{2,20} sr{2,10}	s{2,22} sr{2,11}	s{2,24} sr{2,12}	s{2,2n} sr{2,n}
作为球面镶嵌

参见

• 反棱柱
• 偏方面体

外部链接

• http://mathworld.wolfram.com/Antiprism.html（页面存档备份，存于互联网档案馆）