斯特林公式
数学公式 来自维基百科,自由的百科全书
斯特林公式(英语:Stirling's formula)是一条用来取n阶乘近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特林公式十分好用,而且,即使在n很小的时候,斯特林公式的取值已经十分准确。这个公式以詹姆斯·斯特林的名字命名,虽然亚伯拉罕·棣莫弗早于斯特林提出了一个类似的公式,但结果较不精确。[1][2][3]

阶乘与斯特林公式
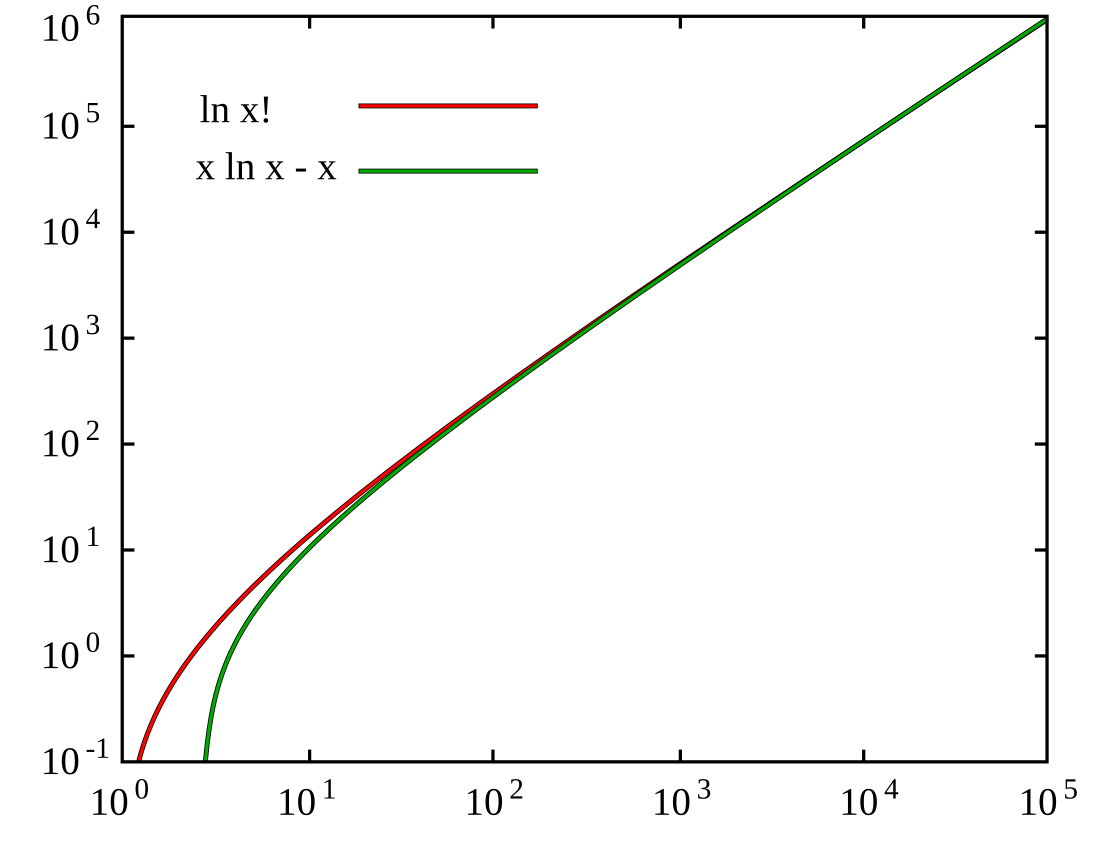
由于已知的技术原因,图表暂时不可用。带来不便,我们深表歉意。 |
(蓝色)、(橘色),数字越大会越趋近。但在负值则会因为出现虚数而无法使用
斯特林公式为:
这就是说,对于足够大的整数n,这两个数互为近似值。更加精确地:
或
历史
这个公式是亚伯拉罕·棣莫弗首先发现的,形式为:
- ,其中c为常量。
斯特林证明了公式中,约为2.506628274631。更加精确的形式是雅克·比内发现的。
推导
这个公式,以及误差的估计,可以推导如下。首先不直接估计n!,而是考虑它的自然对数:
即:
这个方程的右面是积分的近似值(利用梯形法则),而它的误差由欧拉-麦克劳林公式给出:
其中Bk是伯努利数,Rm,n是欧拉-麦克劳林公式中的余项。取极限,可得:
把这个极限记为y。由于欧拉-麦克劳林公式中的余项Rm,n满足:
其中用到了大O符号,与以上的方程结合,便得出对数形式的近似公式:
两边取指数,并选择任何正整数m,便得到了一个含有未知数ey的公式。当m=1时,公式为:
将上述表达式代入沃利斯乘积公式,并令n趋于无穷,便可以得出ey()。因此,我们便得出斯特林公式:
这个公式也可以反复使用分部积分法来得出,首项可以通过最速下降法得到。把以下的和
用积分近似代替,可以得出不含的因子的斯特林公式(这个因子通常在实际应用中无关):
考虑如下近似关系:
以及阶乘的积分形式(Γ函数):
其中被积函数取对数后求导结果可写成:
因此被积函数只有在附近才趋于平稳,现令且,并改写成如下形式:
于是有:
因此可以得到:
两边同时作指数函数运算,变成:
代入到阶乘的积分表示形式,得到:
约等号后侧得到的是高斯积分的形式,计算该积分得出斯特林公式:
收敛速率和误差估计

更加精确的近似公式为:
其中:
斯特林公式实际上是以下级数(现在称为斯特林级数)的第一个近似值:
当时,截断级数的误差等于第一个省略掉的项。这是渐近展开式的一个例子。它不是一个收敛级数;对于任何特殊值n,级数的准确性只在取有限个项时达到最大,如果再取更多的项,则准确性将变得越来越差。
阶乘的对数的渐近展开式也称为斯特林级数:
在这种情况下,级数的误差总是与第一个省略掉的项异号,且最多同大小。
伽玛函数的斯特林公式
对于所有正整数,有:
然而,伽玛函数与阶乘不一样,它对于所有复数都有定义。尽管如此,斯特林公式仍然适用。如果,那么:
反复使用分部积分法,可得以下渐近展开式:
其中Bn是第n个伯努利数。当,其中ε是正数时,这个公式对于绝对值足够大的z是适用的,当使用了最初m个项时,误差项为。对应的近似值可以写为:
斯特林公式的收敛形式
欲得出斯特林公式的一个收敛形式,我们必须计算:
一种方法是利用含有上升阶乘幂的级数。如果,那么:
其中:
从中可以得出斯特林级数的一个收敛形式:
它在时收敛。
适用于计算器的形式
以下的近似值
或
可以通过把斯特林公式整理,并注意到它的幂级数与双曲正弦函数的泰勒级数展开式的相似性来得出。当z的实数部分大于8时,这个近似值精确到小数点后8位。2002年,Robert H. Windschitl建议计算器用这个公式来计算伽玛函数。
Gergő Nemes在2007年提出了一个近似公式,它的精确度与Windschitl的公式相等,但更加简单:
或
参考文献
Wikiwand - on
Seamless Wikipedia browsing. On steroids.















![{\displaystyle n!=e^{y}{\sqrt {n}}~{\left({\frac {n}{e}}\right)}^{n}\left[1+O\left({\frac {1}{n}}\right)\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9531b94acc115896354d5367ecd0fadcb39a0c94)

![{\displaystyle n!={\sqrt {2\pi n}}~{\left({\frac {n}{e}}\right)}^{n}\left[1+O\left({\frac {1}{n}}\right)\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e8d16f782dd8b2a20201c8e71098bfeae9d1a772)










![{\displaystyle {\begin{aligned}\ln(n+\xi )&=\ln \left[n\left(1+{\frac {\xi }{n}}\right)\right]=\ln n+\ln \left(1+{\frac {\xi }{n}}\right)\\&=\ln n+{\frac {\xi }{n}}-{\frac {\xi ^{2}}{2n^{2}}}+\cdots \end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d269e0109207ce1dbe9d0d601364da2f67577012)















![{\displaystyle \Gamma (z)={\sqrt {\frac {2\pi }{z}}}~{\left({\frac {z}{e}}\right)}^{z}\left[1+O\left({\frac {1}{z}}\right)\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c05838078d1fbcbbf91838d8e3b425b8d8d96a8f)







![{\displaystyle 2\ln \Gamma (z)\approx \ln(2\pi )-\ln z+z\left[2\ln z+\ln \left(z\sinh {\frac {1}{z}}+{\frac {1}{810z^{6}}}\right)-2\right],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/30633c9797d1e36b93264d97268306b091387883)
![{\displaystyle \Gamma (z)\approx {\sqrt {\frac {2\pi }{z}}}\left[{\frac {1}{e}}\left(z+{\frac {1}{12z-{\frac {1}{10z}}}}\right)\right]^{z},}](http://wikimedia.org/api/rest_v1/media/math/render/svg/937f1cfd364e52061af08ff888dbb2a53b37eeca)
![{\displaystyle \ln \Gamma (z)\approx {\frac {1}{2}}\left[\ln(2\pi )-\ln z\right]+z\left[\ln \left(z+{\frac {1}{12z-{\frac {1}{10z}}}}\right)-1\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/eaca7a677fd1cac3d22c260b9adc4f09f6db3258)