Функція розподілу простих чисел

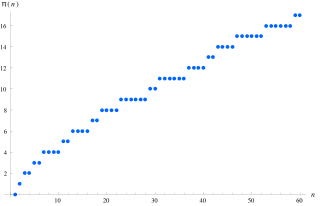
У математиці функція розподілу простих чисел, або пі-функція ${\displaystyle \pi (x)}$, — це функція, що дорівнює числу простих чисел, менших або рівних дійсному числу x^[1][2]. Позначається ${\displaystyle \pi (x)}$ (це ніяк не пов'язано з числом пі).

Значення пі-функції для перших 60 натуральних чисел

Історія

Великий інтерес у теорії чисел викликає швидкість зростання пі-функції^[3][4]. Наприкінці XVIII століття Гаусс і Лежандр висунули припущення, що пі-функція оцінюється як

${\displaystyle {\frac {x}{\ln x}}}$

тобто, що

${\displaystyle \lim \limits _{x\to +\infty }{\frac {\pi (x)}{x/\ln x}}=1.}$

Це твердження — теорема про розподіл простих чисел. Воно еквівалентне твердженню

${\displaystyle \lim \limits _{x\to +\infty }{\frac {\pi (x)}{\operatorname {li} (x)}}=1}$

де ${\displaystyle \operatorname {li} }$ — інтегральний логарифм. Теорему про прості числа вперше довів 1896 року Жак Адамар і незалежно Валле-Пуссен, використовуючи дзета-функцію Рімана, яку 1859 року ввів Ріман.

Точніше зростання ${\displaystyle \pi (x)}$ зараз описують як

${\displaystyle \pi (x)=\operatorname {li} (x)+O{\bigl (}xe^{-{\sqrt {\ln x}}/15}{\bigr )}}$

де ${\displaystyle O}$ позначає O велике. Коли x не дуже велике, ${\displaystyle \operatorname {li} (x)}$ перевищує ${\displaystyle \pi (x)}$, проте різниця ${\displaystyle \pi (x)-\operatorname {li} (x)}$ змінює свій знак нескінченне число разів, найменше натуральне число, для якого відбувається зміна знака, називається числом Ск'юза.

Доведення теореми про прості числа, що не використовують дзета-функції або комплексного аналізу, знайшли 1948 року Атле Сельберг і Пал Ердеш (здебільшого незалежно)^[5].

Таблиці для пі-функції, x/ln x і li(x)

У таблиці показано зростання функцій ${\displaystyle \pi (x),{\frac {x}{\ln x}},\operatorname {li} (x)}$ за степенями 10^[3][6][7][8].

x	π(x)	π(x) − x / ln x	li(x) − π(x)	x / π(x)	π(x)/x (частка простих чисел)
10	4	−0,3	2,2	2,500	40 %
102	25	3,3	5,1	4,000	25 %
103	168	23	10	5,952	16,8 %
104	1 229	143	17	8,137	12,3 %
105	9 592	906	38	10,425	9,59 %
106	78 498	6 116	130	12,740	7,85 %
107	664 579	44 158	339	15,047	6,65 %
108	5 761 455	332 774	754	17,357	5,76 %
109	50 847 534	2 592 592	1 701	19,667	5,08 %
1010	455 052 511	20 758 029	3 104	21,975	4,55 %
1011	4 118 054 813	169 923 159	11 588	24,283	4,12 %
1012	37 607 912 018	1 416 705 193	38 263	26,590	3,76 %
1013	346 065 536 839	11 992 858 452	108 971	28,896	3,46 %
1014	3 204 941 750 802	102 838 308 636	314 890	31,202	3,20 %
1015	29 844 570 422 669	891 604 962 452	1 052 619	33,507	2,98 %
1016	279 238 341 033 925	7 804 289 844 393	3 214 632	35,812	2,79 %
1017	2 623 557 157 654 233	68 883 734 693 281	7 956 589	38,116	2,62 %
1018	24 739 954 287 740 860	612 483 070 893 536	21 949 555	40,420	2,47 %
1019	234 057 667 276 344 607	5 481 624 169 369 960	99 877 775	42,725	2,34 %
1020	2 220 819 602 560 918 840	49 347 193 044 659 701	222 744 644	45,028	2,22 %
1021	21 127 269 486 018 731 928	446 579 871 578 168 707	597 394 254	47,332	2,11 %
1022	201 467 286 689 315 906 290	4 060 704 006 019 620 994	1 932 355 208	49,636	2,01 %
1023	1 925 320 391 606 803 968 923	37 083 513 766 578 631 309	7 250 186 216	51,939	1,92 %
1024	18 435 599 767 349 200 867 866	339 996 354 713 708 049 069	17 146 907 278	54,243	1,84 %
1025	176 846 309 399 143 769 411 680	3 128 516 637 843 038 351 228	55 160 980 939	56,546	1,77 %
1026	1 699 246 750 872 437 141 327 603	28 883 358 936 853 188 823 261	155 891 678 121	58,850	1,70 %
1027	16 352 460 426 841 680 446 427 399	267 479 615 610 131 274 163 365	508 666 658 006	61,153	1,64 %

В OEIS перша колонка значень ${\displaystyle \pi (x)}$ — це послідовність A006880, ${\displaystyle \pi (x)-\left\lfloor {\frac {x}{\ln x}}+0{,}5\right\rfloor }$ — послідовність A057835, а ${\displaystyle \lfloor \operatorname {li} (x)+0{,}5\rfloor -\pi (x)}$ — послідовність A057752.

Алгоритми обчислення пі-функції

Простий спосіб знайти ${\displaystyle \pi (x)}$, якщо ${\displaystyle x}$ не дуже велике, — скористатися решетом Ератосфена, яке видає прості, що не перевищують ${\displaystyle x}$, і підрахувати їх.

Більш продуманий спосіб обчислення ${\displaystyle \pi (x)}$ запропонував Лежандр: дано ${\displaystyle x}$, якщо ${\displaystyle p_{1},p_{2},\ldots ,p_{k}}$ — різні прості числа, число цілих чисел, що не перевищують ${\displaystyle x}$ і не діляться на всі ${\displaystyle p_{i}}$ дорівнює

${\displaystyle \lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots }$

(де ${\displaystyle \lfloor \cdots \rfloor }$ позначає цілу частину). Отже, отримане число дорівнює

${\displaystyle \pi (x)-\pi \left({\sqrt {x}}\right)+1}$

якщо ${\displaystyle p_{1},p_{2},\ldots ,p_{k}}$ — це всі прості числа, що не перевищують ${\displaystyle {\sqrt {x}}}$.

У 1870—1885 роках у серії статей Ернст Майссель^[ru] описав (і використав) практичний комбінаторний спосіб обчислення ${\displaystyle \pi (x)}$. Нехай ${\displaystyle p_{1},p_{2},\ldots ,p_{n}}$ — перші ${\displaystyle n}$ простих, позначимо ${\displaystyle \Phi (m,n)}$ кількість натуральних чисел, що не перевищують ${\displaystyle m}$, які не діляться на жодне ${\displaystyle p_{i}}$. Тоді

${\displaystyle \Phi (m,n)=\Phi (m,n-1)-\Phi \left(\left[{\frac {m}{p_{n}}}\right],n-1\right)}$

Візьмемо натуральне ${\displaystyle m}$, якщо ${\displaystyle n=\pi \left({\sqrt[{3}]{m}}\right)}$ і якщо ${\displaystyle \mu =\pi \left({\sqrt {m}}\right)-n}$, то

${\displaystyle \pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right)}$

Використовуючи цей підхід, Майссель вирахував ${\displaystyle \pi (x)}$ для ${\displaystyle x=5\cdot 10^{5};10^{6};10^{7};10^{8}}$.

1959 року Деррік Генрі Лемер^[en] розширив і спростив метод Майсселя. Визначимо, для дійсного ${\displaystyle m}$ та для натуральних ${\displaystyle n,k}$ величину ${\displaystyle P_{k}(m,n)}$ як кількість чисел, що не перевищують m і мають рівно k простих множників, причому всі вони перевищують ${\displaystyle p_{n}}$. Крім того, нехай ${\displaystyle P_{0}(m,n)=1}$. Тоді

${\displaystyle \Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n)}$

де сума явно завжди має скінченне число ненульових доданків. Нехай ${\displaystyle y}$ — ціле, таке, що ${\displaystyle {\sqrt[{3}]{m}}\leqslant y\leqslant {\sqrt {m}}}$, і нехай ${\displaystyle n=\pi (y)}$. Тоді ${\displaystyle P_{1}(m,n)=\pi (m)-n}$ і ${\displaystyle P_{k}(m,n)=0}$ при ${\displaystyle k\geqslant 3}$. Отже

${\displaystyle \pi (m)=\Phi (m,n)+n-1-P_{2}(m,n)}$

Обчислення ${\displaystyle P_{2}(m,n)}$ можна отримати так:

${\displaystyle P_{2}(m,n)=\sum _{y<p\leqslant {\sqrt {m}}}\left(\pi \left({\frac {m}{p}}\right)-\pi (p)+1\right)}$

З іншого боку, обчислити ${\displaystyle \Phi (m,n)}$ можна за допомогою таких правил:

1. ${\displaystyle \Phi (m,0)=\lfloor m\rfloor }$
2. ${\displaystyle \Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right)}$

Використовуючи цей метод і IBM 701, Лемер зумів обчислити ${\displaystyle \pi \left(10^{10}\right)}$.

Надалі цей метод вдосконалили Lagarias, Miller, Odlyzko, Deleglise та Rivat^[9].

Китайський математик Hwang Cheng використав такі тотожності:^[10]

${\displaystyle e^{(a-1)\Theta }f(x)=f(ax),}$

${\displaystyle J(x)=\sum _{n=1}^{\infty }{\frac {\pi (x^{1/n})}{n}}}$

і, вважаючи ${\displaystyle x=e^{t}}$, виконуючи перетворення Лапласа обох частин і застосовуючи суму геометричної прогресії з ${\displaystyle e^{n\Theta }}$, отримав вираз:

${\displaystyle {\frac {1}{2{\pi }i}}\int _{c-i\infty }^{c+i\infty }g(s)t^{s}\,ds=\pi (t)}$

${\displaystyle {\frac {\ln \zeta (s)}{s}}=(1-e^{\Theta (s)})^{-1}g(s)}$

${\displaystyle \Theta (s)=s{\frac {d}{ds}}}$

Інші функції, що підраховують прості числа

Інші функції, що підраховують прості числа, також використовують, оскільки з ними зручніше працювати. Одна з них — функція Рімана, яку часто позначають як ${\displaystyle \Pi _{0}(x)}$ або ${\displaystyle J_{0}(x)}$. Вона має стрибок на 1/n для степенів простих ${\displaystyle p^{n}}$, причому в точці стрибка ${\displaystyle x}$ її значення дорівнює півсумі значень по обидва боки від ${\displaystyle x}$. Ці додаткові деталі потрібні для того, щоб її можна було визначити зворотним перетворенням Мелліна. Формально визначимо ${\displaystyle \Pi _{0}(x)}$ як

${\displaystyle \Pi _{0}(x)={\frac {1}{2}}{\bigg (}\sum _{p^{n}<x}{\frac {1}{n}}\ +\sum _{p^{n}\leq x}{\frac {1}{n}}{\bigg )}}$

де p просте.

Також можна записати

${\displaystyle \Pi _{0}(x)=\sum \limits _{n=2}^{x}{\frac {\Lambda (n)}{\ln n}}-{\frac {1}{2}}{\frac {\Lambda (x)}{\ln x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}({\sqrt[{n}]{x}})}$

де ${\displaystyle \Lambda (n)}$ — функція Мангольдта та

${\displaystyle \pi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )}{2}}.}$

Формула обернення Мебіуса дає

${\displaystyle \pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi _{0}({\sqrt[{n}]{x}})}$

Використовуючи відоме співвідношення між логарифмом дзета-функції Рімана та функцією Мангольдта ${\displaystyle \Lambda }$, і використовуючи формулу Перрона отримаємо

${\displaystyle \ln \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s-1}\,dx}$

Функція Рімана має твірну функцію

${\displaystyle \sum _{n=1}^{\infty }\Pi _{0}(n)x^{n}=\sum _{a=2}^{\infty }{\frac {x^{a}}{1-x}}-{\frac {1}{2}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }{\frac {x^{ab}}{1-x}}+{\frac {1}{3}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }{\frac {x^{abc}}{1-x}}-{\frac {1}{4}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }\sum _{d=2}^{\infty }{\frac {x^{abcd}}{1-x}}+\cdots }$

Функції Чебишова^[en] — це функції, що підраховують степені простих чисел ${\displaystyle p^{n}}$ з вагою ${\displaystyle \ln p}$:

${\displaystyle \theta (x)=\sum _{p\leqslant x}\ln p}$

${\displaystyle \psi (x)=\sum _{p^{n}\leqslant x}\ln p=\sum _{n=1}^{\infty }\theta ({\sqrt[{n}]{x}})=\sum _{n\leqslant x}\Lambda (n).}$

Формули для функцій, що підраховують прості числа

Формули для функцій, які підраховують прості числа, бувають двох видів: арифметичні формули та аналітичні формули. Аналітичні формули для таких функцій вперше використано для доведення теореми про прості числа. Вони походять від робіт Рімана і Мангольдта^[de] і загалом відомі як явні формули^[11].

Існує такий вираз для ${\displaystyle \psi }$ -функції Чебишова:

${\displaystyle \psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-\ln 2\pi -{\frac {1}{2}}\ln(1-x^{-2})}$

де

${\displaystyle \psi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\psi (x-\varepsilon )+\psi (x+\varepsilon )}{2}}.}$

Тут ${\displaystyle \rho }$ пробігає нулі дзета-функції в критичній смузі, де дійсна частина ${\displaystyle \rho }$ лежить між нулем та одиницею. Формула істинна для всіх ${\displaystyle x>1}$. Ряд за коренями збігається умовно, і його можна взяти в порядку абсолютного значення зростання уявної частини коренів. Зауважимо, що аналогічна сума за тривіальними коренями дає останній доданок у формулі.

Для ${\displaystyle \Pi _{0}(x)}$ маємо таку складну формулу

${\displaystyle \Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} (x^{\rho })-\ln 2+\int _{x}^{\infty }{\frac {dt}{t(t^{2}-1)\ln t}}.}$

Знову ж, формула істинна для всіх ${\displaystyle x>1}$, де ${\displaystyle \rho }$ — нетривіальні нулі дзета-функції, впорядковані за їхнім абсолютним значенням, і, знову, останній інтеграл береться зі знаком «мінус» і є такою самою сумою, але за тривіальними нулями. Вираз ${\displaystyle \operatorname {li} (x^{\rho })}$ у другому члені можна розглянути як ${\displaystyle \operatorname {Ei} (\rho \ln x)}$, де ${\displaystyle \operatorname {Ei} }$ — аналітичне продовження інтегральної показникової функції на комплексну площину з гілкою, вирізаною вздовж прямої ${\displaystyle x<0}$.

Отже, формула обернення Мебіуса дає нам^[12]

${\displaystyle \pi _{0}(x)=\operatorname {R} (x)-\sum _{\rho }\operatorname {R} (x^{\rho })-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\mathop {\mathrm {arctg} } {\frac {\pi }{\ln x}}}$

істинне для ${\displaystyle x>1}$, де

${\displaystyle \operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} (x^{1/n})=1+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k!k\zeta (k+1)}}}$

називається R-функцією також на честь Рімана.^[13] Останній ряд у ній відомий як ряд Грама^[en][14] і збігається для всіх ${\displaystyle x>0}$.

Сума за нетривіальними нулями дзета-функції у формулі для ${\displaystyle \pi _{0}(x)}$ описує флуктуації ${\displaystyle \pi _{0}(x)}$, тоді як інші доданки дають гладку частину пі-функції,^[15] тому можна використати

${\displaystyle \operatorname {R} (x)-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\mathop {\mathrm {arctg} } {\frac {\pi }{\ln x}}}$

як найкраще наближення для ${\displaystyle \pi (x)}$ для ${\displaystyle x>1}$.

Амплітуда «шумної» частини евристично оцінюється як ${\displaystyle {\sqrt {x}}/\ln x}$ тому флуктуації в розподілі простих можна явно представити ${\displaystyle \Delta }$-функцією:

${\displaystyle \Delta (x)=\left(\pi _{0}(x)-\operatorname {R} (x)+{\frac {1}{\ln x}}-{\frac {1}{\pi }}\mathop {\mathrm {arctg} } {\frac {\pi }{\ln x}}\right){\frac {\ln x}{\sqrt {x}}}.}$

Великі таблиці значень ${\displaystyle \Delta (x)}$ доступні тут^[7].

Нерівності

Тут виписано деякі нерівності для ${\displaystyle \pi (x)}$.

${\displaystyle {\frac {x}{\ln x}}<\pi (x)<1{,}25506\cdot {\frac {x}{\ln x}}\qquad x\geqslant 17.}$

Ліва нерівність виконується при ${\displaystyle x\geqslant 17}$, а права — при ${\displaystyle x>1.}$^[16]

Нерівності для ${\displaystyle n}$-го простого числа ${\displaystyle p_{n}}$:

${\displaystyle n\ln n+n\ln \ln n-3/2\cdot n<p_{n}<n\ln n+n\ln \ln n,\ n\geqslant 6.}$

Ліва нерівність істинна при ${\displaystyle n\geqslant 2}$, а права — при ${\displaystyle n\geqslant 6}$.

Має місце така асимптотика для ${\displaystyle n}$-го простого числа ${\displaystyle p_{n}}$:

${\displaystyle p_{n}=n\ln n\left(1+{\frac {\ln \ln n-1}{\ln n}}+{\frac {\ln \ln n-2}{\ln ^{2}n}}+{\frac {-1/2\ln ^{2}\ln n+3\ln \ln n-11/2}{\ln ^{3}n}}+O\left({\frac {\ln ^{3}\ln n}{\ln ^{4}n}}\right)\right)}$

Гіпотеза Рімана

Гіпотеза Рімана еквівалентна точнішій межі помилки наближення ${\displaystyle \pi (x)}$ інтегральним логарифмом, а отже й регулярнішому розподілу простих чисел

${\displaystyle \pi (x)=\operatorname {li} (x)+O({\sqrt {x}}\ln x).}$

Зокрема,^[17]

${\displaystyle |\pi (x)-\operatorname {li} (x)|<{\frac {1}{8\pi }}{\sqrt {x}}\,\ln x,\qquad x\geqslant 2657.}$

Див. також

• Теорема про розподіл простих чисел
• Постулат Бертрана
• Число Ск'юза

Примітки

1. Bach, Eric; Shallit, Jeffrey. Section 8.8 // Algorithmic Number Theory. — MIT Press, 1996. — Т. 1. — С. 234. — ISBN 0-262-02405-5.
2. Weisstein, Eric W. Prime Counting Function(англ.) на сайті Wolfram MathWorld.
3. How many primes are there?. Chris K. Caldwell. Архів оригіналу за 20 вересня 2012. Процитовано 2 грудня 2008. [Архівовано 2012-10-15 у Wayback Machine.]
4. Dickson, Leonard Eugene^[en]. History of the Theory of Numbers I: Divisibility and Primality. — Dover Publications, 2005. — ISBN 0-486-44232-2.
5. K. Ireland, M. Rosen. A Classical Introduction to Modern Number Theory. — Second. — Springer, 1998. — ISBN 0-387-97329-X.
6. Tables of values of pi(x) and of pi2(x). Tomas Oliveira e Silva. Архів оригіналу за 20 вересня 2012. Процитовано 14 вересня 2008.
7. Values of π(x) and Δ(x) for various x's. Andrey V. Kulsha. Архів оригіналу за 20 вересня 2012. Процитовано 14 вересня 2008.
8. A table of values of pi(x). Xavier Gourdon, Pascal Sebah, Patrick Demichel. Архів оригіналу за 20 вересня 2012. Процитовано 14 вересня 2008.
9. Computing ?(x): The Meissel, Lehmer, Lagarias, Miller, Odlyzko method (PDF). Marc Deleglise and Joel Rivat, Mathematics of Computation, vol. 65, number 33, January 1996, pages 235–245. Архів (PDF) оригіналу за 20 вересня 2012. Процитовано 14 вересня 2008.
10. Hwang H., Cheng (2001). Demarches de la Geometrie et des Nombres de l'Universite du Bordeaux. Prime Magic conference.
11. Titchmarsh, E.C. The Theory of Functions, 2nd ed. — Oxford University Press, 1960.
12. Riesel, Hans^[en]; Gohl, Gunnar. Some calculations related to Riemann's prime number formula // Mathematics of Computation^[en] : journal. — American Mathematical Society, 1970. — Vol. 24, no. 112 (23 December). — P. 969—983. — ISSN 0025-5718. — DOI:10.2307/2004630.
13. Weisstein, Eric W. Riemann Prime Counting Function(англ.) на сайті Wolfram MathWorld.
14. Weisstein, Eric W. Gram Series(англ.) на сайті Wolfram MathWorld.
15. The encoding of the prime distribution by the zeta zeros. Matthew Watkins. Архів оригіналу за 20 вересня 2012. Процитовано 14 вересня 2008. [Архівовано 2013-02-04 у Wayback Machine.]
16. Rosser, J. Barkley^[en]; Schoenfeld, Lowell. Approximate formulas for some functions of prime numbers // Illinois J. Math. : journal. — 1962. — Vol. 6 (23 December). — P. 64—94. — ISSN 0019-2082. Архівовано з джерела 28 лютого 2019.
17. Lowell Schoenfeld. Sharper bounds for the Chebyshev functions θ(x) and ψ(x). II // Mathematics of Computation^[en] : journal. — American Mathematical Society, 1976. — Vol. 30, no. 134 (23 December). — P. 337—360. — ISSN 0025-5718. — DOI:10.2307/2005976.

Література

• К. Прахар. Распределение простых чисел. — Мир, 1967.
• В. И. Зенкин. Распределение простых чисел. Элементарные методы. Калининград, 2008.

Посилання

• Chris Caldwell, The Nth Prime Page на сайті Prime Pages^[en].