Метрика Шварцшильда

Метрика Шварцшильда (англ. Schwarzschild metric)— розв'язок рівнянь Ейнштейна для сферично-симетричного розподілу мас у порожнечі за межами мас, що описує викривлений простір-час навколо масивного тіла. Цей розв'язок рівнянь Ейнштейна отримав у 1916 році Карл Шварцшильд. Його важливість у тому, що він теоретично визначив можливість утворення чорних дір.

У Вікіпедії є статті про інші значення цього терміна: Метрика.

Простір Шварцшильда. Математичний образ кротовини за Шварцшильдом.

У метриці Шварцшильда просторово-часовий інтервал задається формулою:

${\displaystyle ds^{2}=\left(1-{\frac {R_{g}}{r}}\right)c^{2}dt^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2})-{\frac {dr^{2}}{1-R_{g}/r}}}$.

У цій формулі ${\displaystyle R_{g}={\frac {2MG}{c^{2}}}}$ — гравітаційний радіус. Метрика залежить тільки від повної маси тіл M. Інші величини у формулі: G — гравітаційна стала, c — швидкість світла.

Метрика Шварцшильда справедлива не лише для нерухомого тіла, а й для тіла, що може розширятися чи стискатися — необхідно тільки, щоб воно залишалося сферично симетричним.

Для отримання метрики всередині гравітаційних мас необхідно знати розподіл їхньої густини в просторі або рівняння стану.

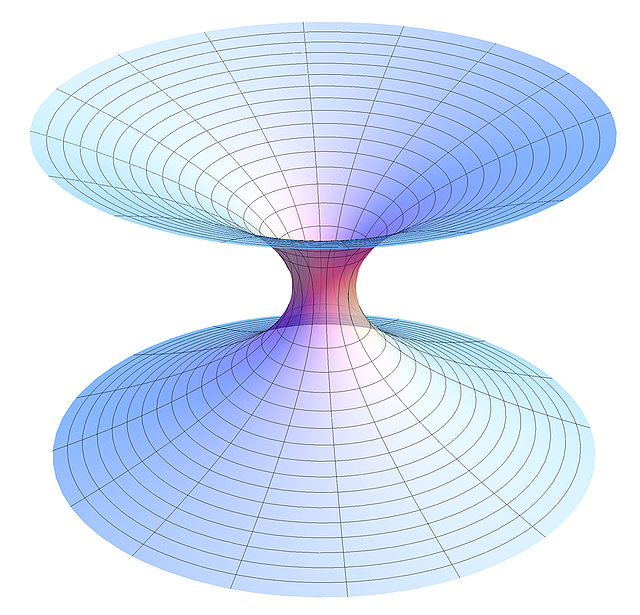
Викривлення простору

Викривлення простору можна проілюструвати тим фактом, що віддаль між двома точками ${\displaystyle r_{1}}$ і ${\displaystyle r_{2}}$ на одному промені дорівнює

${\displaystyle \int _{r_{1}}^{r_{2}}{\frac {dr}{\sqrt {1-R_{g}/r}}}}$

і більша за ${\displaystyle r_{2}-r_{1}}$. Це аналогічно тому, як довжина відрізка кола між двома точками на колі більша за довжину хорди, що сполучає їх.

Значення

Метрика Шварцшильда дозволила визначити викривлення шляху світлового променя поблизу масивного тіла, що стало одним із експериментальних підтверджень загальної теорії відносності.

Крім того, аналіз стану масивного тіла показує, що за достатньо великої маси, для такого тіла може не існувати стаціонарного радіуса, воно стискатиметься. Процес стиснення отримав назву гравітаційного колапсу.

Див. також

• Простір Мінковського
• Метрика Шварцшильда — де Сіттера^[en]
• Чорна діра
• Координати Леметра
• Діаграма Крускала — Секереша
• Задача Кеплера в загальній теорії відносності

Джерела

• Ландау Л.Д., Лившиц Е.М. (1974). Теоретическая физика. т. ІІ. Теория поля. Москва: Наука.