பெருக்கல் (கணிதம்)

கணிதத்தில் பெருக்கல் (Multiplication) என்பது ஒரு அடிப்படையான கணிதச் செயல் ஆகும். கழித்தல், கூட்டல், வகுத்தல் ஆகியவை ஏனைய மூன்று கணித அடிப்படைச் செயல்களாகும். பெருக்கப்படும் இரண்டு எண்களில் ஒன்று முழு எண்ணாக இருப்பின், அவ்வெண்களின் பெருக்கல், அம் முழு எண்ணின் எண்ணிக்கையளவு தடவை மற்ற எண்ணின் தொடர்ச்சியான கூட்டலாகும்.

${\displaystyle {{a\times n=} \atop {\ }}{{\underbrace {a+\cdots +a} } \atop n}}$

ஒரு பைக்கு 3 கோலிகள் வீதம் நான்கு பைகளில் உள்ள மொத்த கோலிகள் 12 (4 × 3 = 12).

பெருக்கலை அளவிடுதலாகவும் கருதலாம். படத்தில் 2 ஐ 3 ஆல் பெருக்குதலின் விடை, அளவிடுதல் மூலம் 6 எனக் கிடைக்கிறது.

2 × 3 = 6 என்ற பெருக்கலின் அசைபடம்.

4 × 5 = 20. பெரிய செவ்வகத்துக்குள் 1 x 1 அளவு கொண்ட 20 சதுரங்கள் உள்ளன.

துணியின் பரப்பளவு 4.5m × 2.5m = 11.25m²; 4½ × 2½ = 11¼

எடுத்துக்காட்டாக, 7 × 4 என்பது, 7 + 7 + 7 + 7, அல்லது 4 + 4 + 4 + 4 + 4 + 4 + 4 (நான்கு ஏழுகள் அல்லது ஏழு நான்குகள் = 28) என்பதற்குச் சமனாகும். ${\displaystyle 7\times 4=4+4+4+4+4+4+4=28}$

இதில் 7 மற்றும் 4 இரண்டும் காரணிகள் எனவும் 28 பெருக்குத்தொகை எனவும் அழைக்கப்படும். இரண்டு பின்னங்களை ஒன்றுடன் ஒன்று பெருக்கும்போது கிடைக்கும் விடையின் பகுதியும், விகுதியும், பெருக்கப்பட்ட பின்னங்களின் பகுதிகளின் பெருக்கமாகவும், விகுதிகளின் பெருக்கமாகவும் அமையும்.

எடுத்துக் காட்டாக,
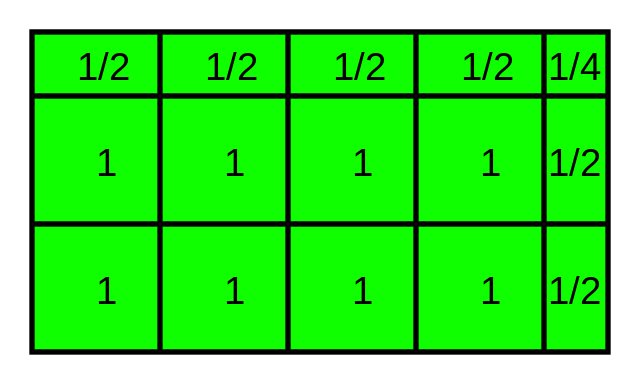
a/b × c/d = (ac)/(bd). அதுபோலவே, 2/3 × 3/4 = (2×3)/(3×4) = 6/12 = 1/2.

பெருக்கலின் முக்கியப் பண்பு பரிமாற்றுத் தன்மையாகும். பெருக்கப்படும் இரு எண்களின் வரிசை மாறினாலும் பெருக்குத்தொகையில் மாற்றமிருக்காது.

${\displaystyle 4\times 3=3+3+3+3=12}$

${\displaystyle 3\times 4=4+4+4=12}$

நேர்ம முழுஎண்களின் பெருக்கலை செவ்வகமாக அடுக்கப்பட்ட பொருட்களின் எண்ணிக்கையாக அல்லது அச்செவ்வகத்தின் பரப்பளவாகக் கொள்ளலாம். பெருக்கலின் பரிமாற்றுத் தன்மையின் காரணமாக பரப்பளவு காண்பதற்காக, செவ்வகத்தின் எப்பக்கம் முதலில் அளக்கப்படுகிறது என்பது முக்கியமில்லை.

பெருக்கலின் நேர்மாறு செயல் வகுத்தலாகும். எடுத்துக்காட்டாக 3 x 4 =12; 12 ஐ 3 ஆல் வகுக்க 4 உம், 4 ஆல் வகுக்க 3 உம் விடையாகக் கிடைக்கும். ஒரு எண்ணை 3 ஆல் பெருக்கிக் கிடைக்கும் விடையை மீண்டும் 3 ஆல் வகுத்தால் பழைய எண்ணே விடையாகக் கிடைக்கும்.

சிக்கலெண்கள் போன்ற பிறவகை எண்களுக்கும் அணிகள் போன்றவற்றுக்கும் பெருக்கல் வரையறுக்கப்பட்டுள்ளது.

குறியீடும் தொடர்பான சொற்களும்

பெருக்கல் குறி

பெருக்கல், பெருக்கல் குறி எனப்படும் "x" மூலம் குறிக்கப்படுகின்றது.^[1] இது பெருக்கப்பட வேண்டிய எண்களுக்கு இடையே எழுதப்படுகின்றது (எகா: 3 x 4). பெருக்கலின் மூலம் கிடைக்கும் விளைவு, அதாவது பெருக்குத்தொகை, சமன் குறியுடன் எழுதப்படும். எடுத்துக் காட்டாக:

${\displaystyle 3\times 2=6}$

${\displaystyle 2\times 2=4}$

${\displaystyle 5\times 2=10}$

• பெருக்கப்படும் இரு எண்களுக்கிடையே முற்றுப்புள்ளி (.) குறியிட்டும் பெருக்கல் குறிக்கப்படுகிறது.^[2]

${\displaystyle 5\cdot 2\quad {\text{or}}\quad 5\,.\,2}$

• இயற்கணிதத்தில், இரு மாறிகளின் பெருக்கல் இரண்டுக்குமிடையே எந்தவொரு குறியும் இல்லாமல் அவையிரண்டையும் அடுத்தடுத்து எழுதும்முறையில் குறிக்கப்படுகிறது.

x மடங்கு y என்பதற்கு xy ; x இன் 5 மடங்கு என்பதற்கு 5x என்றும் எழுதப்படுகிறது.^[3] அடைப்புக்குறிக்குள் எழுதப்படும் கணியங்களின் பெருக்கலையும் இம்முறையில் எழுதலாம். எழுத்துக்காட்டாக, 5 x 2 = 5(2) அல்லது (5)(2).

• திசையன்களின் பெருக்கலில் 'x' மற்றும் '${\displaystyle \cdot }$' குறியீடுகளில் வேறுபாடு உள்ளது. இரு திசையன்களின் குறுக்குப் பெருக்கலில் 'x' குறியீடும், புள்ளிப் பெருக்கலுக்கு '${\displaystyle \cdot }$' குறியீடும் பயன்படுத்தப்படுகிறது.

கணினி நிரலாக்கத்தில், "உடுக்குக்குறி" பெருக்கலின் குறியீடாகப் பயன்படுத்தப்படுகிறது. (5*2)

பொதுவாக,பெருக்கப்படவேண்டிய எண்கள் "காரணிகள்" என அழைக்கப்படுகின்றன. பெருக்கப்பட வேண்டிய எண் "பெருக்கபடுமெண்" ("multiplicand") என்றும் பெருக்கும் எண் "பெருக்கி" அல்லது "பெருக்கு எண்" ("multiplier") என்றும் அழைக்கப்படுகிறது. வழக்கமாக ஒரு பெருக்கலில்,பெருக்கி முதலிலும், பெருக்குபடுவெண் இரண்டாவதாகவும் எழுதப்படும்.^[4] (though this can vary by language^[5]). சில சமயங்களில் மாற்றி எழுதப்படுவதும் உண்டு.^[6] மேலும் சில இடங்களில் "காரணி" என்ற சொல்லுக்கு ஒத்ததாக "பெருக்குபடுமெண்" கருதப்படுகிறது..^[7] இயற்கணிதத்தில் ஒரு மாறி அல்லது கோவையின் பெருக்கு எண்ணானது குணகம் அல்லது கெழு என அழைக்கப்படுகிறது. (3xy² இல் 3 என்பது கெழு).

பெருக்கலில் கிடைக்கும் விடை, பெருக்குத்தொகை என அழைக்கப்படுகிறது. முழுவெண்களின் பெருக்குத்தொகை அப்பெருக்கலின் காரணிகள் ஒவ்வொன்றின் மடங்காக இருக்கும். எடுத்துக்காட்டாக 3, 5 இன் பெருக்குத்தொகை 15; 15, 3 மற்றும் 5 இன் மடங்காக உள்ளதைக் காணலாம்.

கணக்கிடுதல்

வழக்கமாக எண் பெருக்கல், பெருக்கல் வாய்ப்பாடு கொண்டு செய்யப்படுகிறது. பெருக்கும் எண்களின் தசமபின்ன இலக்கங்கள் இரண்டிற்கும் அதிகமாக உள்ளபோது பெருக்கல் சற்று கடினமானதாகவும் பிழை நேரக்கூடியதாகவும் ஆகிறது. இந்தகையப் பெருக்கல்களை எளிதாக்குவதற்கு பொது மடக்கைகள் கண்டுபிடிக்கப்பட்டன. நழுவு சட்டத்தைப் பயன்படுத்தி மூன்று தானங்கள் வரை துல்லியமாகப் பெருக்க இயலும். 20 ஆம் நூற்றாண்டின் துவக்கத்திலிருந்து, கண்டுபிடிக்கப்பட்ட கணிப்பான்களின் உதவியால் 10 இடங்கள்வரைத் துல்லியமாகப் பெருக்குவது எளிதாயிற்று. தற்காலக் கணினிகள் மற்றும் கணிப்பான்களின் உதவியால், பெருக்கல் வாய்ப்பாடின்றி பெரியளவிலான பெருக்கலையும் எளிதாகச் செய்ய முடிகிறது.

வரலாற்று முறைகள்

பண்டைய எகிப்து, பண்டைக் கிரேக்கம், பண்டைய இந்திய மற்றும் பண்டைய சீன வரலாறுப்பதிவுகளில் பெருக்கல் முறைகள் ஆவணப்படுத்தப்பட்டுள்ளன. பழைய கற்காலத்தின் இறுதிப்பகுதியில் நடு ஆப்பிரிக்காவில் பெருக்கல் என்பது அறியப்பட்டிருந்தது என்பதை கிமு 18,000 - 20,000 காலத்திய இஷான்கோ எலும்பு காட்டுகிறது.

எகிப்தியர்கள்

ரைன்ட் கணிதப் பப்பிரசில் ஆவணப்படுத்தப்பட்டுள்ள எகிப்திய பெருக்கல் முறையில், முழுவெண்கள் மற்றும் பின்னங்களின் பெருக்கலில், தொடர் கூட்டல்கள் மற்றும் இரட்டித்தல் பயன்படுத்தப்பட்டுள்ளது.

எடுத்துக்காட்டாக, 13 , 21 இன் பெருக்குத்தொகை காண:

• 21 ஐ மும்முறை இரட்டிக்க வேண்டும்.

2 × 21 = 42;

4 × 21 = 2 × 42 = 84;

8 × 21 = 2 × 84 = 168.

• இரட்டித்த தொடரின் பொருத்தமான இலக்கங்களைக் கூட்டி இறுதிப் பெருக்குத்தொகை பெறப்படுகிறது:

13 × 21 = (1 + 4 + 8) × 21 = (1 × 21) + (4 × 21) + (8 × 21) = 21 + 84 + 168 = 273.

பபிலோனியர்கள்

தற்கால தசம முறையையொத்த, அறுபதின்ம இடஞ்சார் குறியீடு முறையை (sexagesimal)பபிலோனியர்கள் பயன்படுத்தினர். எனவே பாபிலோனியப் பெருக்கல் முறையானது, இன்றையத் தசமப் பெருக்கலை மிகவும் ஒத்திருந்தது. பபிலோனியர்கள் பெருக்கல் வாய்ப்பாடுகளைப் பயன்படுத்தினர். இந்த வாய்ப்பாடுகளில் குறிப்பிட்ட ஒரு முதன்மை எண்ணின் முதல் 20 மடங்குகள் இருந்தன (principal number n: n, 2n, ..., 20n) அதனைத் தொடர்ந்து 10n: 30n 40n, 50n ஆகியவையும் இருந்தன.

அறுபதின்மப் பெருக்கலில்: 53n இன் மதிப்பு காண்பதற்கு:

50n மற்றும் 3n இன் மதிப்புகளை வாய்ப்பாட்டில் இருந்து கண்டுபிடித்து அவற்றைக் கூட்டினால் விடை கிடைத்து விடும்.

சீனர்

38 × 76 = 2888

கோல்களைக் கொண்டு இருவகைகளில் குறிக்கப்படும் சீன எண்ணுருக்கள்

துவக்ககாலத்தில் சீனர்கள் கூட்டல், கழித்தல், பெருக்கல், வகுத்தல் ஆகிய செயல்களுக்கு சிறுகோல்களை இடமதிப்புமுறையில் பயன்படுத்தினர். எனினும் கிமு 300க்கும் முற்பட்ட காலத்தைச் சேர்ந்த கணித நூலான சௌபி சுவான்ஜிங் (Zhoubi Suanjing) மற்றும் கணிதக்கலையில் ஒன்பது அத்தியாயங்கள் (Nine Chapters on the Mathematical Art) என்ற நூலிலும் பெருக்கல் கணக்கீடுகள் வார்த்தைகளில் எழுத்துவடிவில் காணப்படுகின்றன. இடமதிப்பு தசம எண்கணிதத் தீர்வுமுறைகள் முகம்மது இப்னு மூசா அல்-குவாரிஸ்மி எனும் கணிதவியலாளரால் அரபுநாடுகளில் 9 ஆம் நூற்றாண்டின் துவக்கத்தில் அறிமுகப்படுத்தப்பட்டது.

தற்கால முறைகள்

சட்டகப்பின்னல் முறையில் 45, 256 இன் பெருக்கல். 45 × 256 = 11520.

இந்து-அரபு எண்ணுருக்கள் அடிப்படையிலான தற்காலப் பெருக்கல் முறையானது இந்தியக் கணிதவியலாளர் பிரம்மகுப்தரால் விவரிக்கப்பட்டது. பிரம்மகுப்தர் கூட்டல், கழித்தல், பெருக்கல் மற்றும் வகுத்தலின் விதிகளை வகுத்திருந்தார். பிரின்ஸ்டன் பல்கலைக்கழக பேராசிரியரான ஹென்றி புர்ச்சர்டு பைன் (Henry Burchard Fine) என்பவரின் கூற்று:

இந்தியர்கள் இடஞ்சார் தசமமுறையைக் கண்டுபித்தவர்கள் மட்டுமல்லாது, அம்முறையிலுள்ள அடிப்படைக் கணக்கிடும் முறைகளையும் அறிந்திருந்தனர். கூட்டலும் கழித்தலும் தற்காலத்தில் செய்யப்படுவது போலவே அவர்கள் அக்காலத்தில் செய்தனர். பெருக்கலுக்கு அவர்கள் பலமுறைகளைப் பயன்படுத்தினர். அவற்றுள் ஒன்று, தற்போது நாம் பின்பற்றும் பெருக்கல் முறையாகும். ஆனால் வகுத்தலை அவர்கள் கடினப்பட்டுச் செய்தனர்.

^[8]

கட்ட முறை

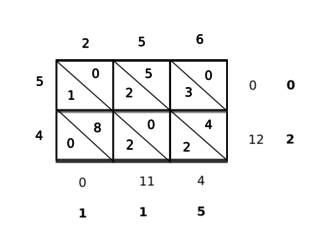
கட்டமுறை அல்லது பெட்டிமுறைப் பெருக்கல் இங்கிலாந்து, அமெரிக்கா போன்ற நாடுகளில் துவக்கப்பள்ளிகளில் பயன்படுத்தப்படுகிறது. இம்முறையில் இலக்கப் பெருக்கல் எவ்வாறு செய்யப்படுகிறது என்பதை எளிதாகப் புரிந்துகொள்ள முடியும்.

34, 13 இன் பெருக்கல் கட்டமுறையில்:

	30	4
10	300	40
3	90	12

பின்னர் கட்டத்துக்கள் அமையும் நான்கு விடைகளையும் கூட்டி இறுதி விடைப் பெறப்படுகிறது.

பண்புகள்

0–10 எண்களின் பெருக்கல். கோடுகள் = பெருக்குபடு எண்கள். X அச்சு = பெருக்கு எண்கள். Y அச்சு = பெருக்குத்தொகை.
இதனை மற்ற காற்பகுதிகளும் நீட்டித்தால் ஒரு எதிர்ம எண்ணை மற்றொரு எதிர்ம எண்ணால் பெருக்கும்போது விடை நேர்ம எண் என்பதை அறியலாம்.

இயல் எண்கள், முழு எண்கள் பின்னங்கள் ஆகியவற்றை உள்ளடக்கிய மெய்யெண்கள் மற்றும் சிக்கலெண்கள் பெருக்கலுக்குக் குறிப்பிட்ட சில பண்புகள் உள்ளன.

• பரிமாற்றுத்தன்மை

பெருக்கப்படும் எண்களின் வரிசை முக்கியமில்லை. அவை மாற்றப்படலாம்:

${\displaystyle x\cdot y=y\cdot x.}$

• சேர்ப்புப் பண்பு

கூட்டல் மற்றும் பெருக்கலை மட்டும் கொண்டிருந்தால் செயலியை அமல்படுத்தும் வரிசை முறை மாறலாம்:

${\displaystyle (x\cdot y)\cdot z=x\cdot (y\cdot z)}$

• பங்கீட்டுப் பண்பு

கூட்டல், பெருக்கல் இரண்டுக்கும் பொருந்தும். இயற்கணிதக் கோவைகளை எளிமையாக்க இப்பண்பு பெரிதும் உதவும்.

${\displaystyle x\cdot (y+z)=x\cdot y+x\cdot z}$

முற்றொருமை உறுப்பு

பெருக்கல் சமனி 1; எந்தவொரு எண்ணும் 1 ஆல் பெருக்கப்படுவதால் மாற்றமே அடைவதில்லை. இது சமனிப்பண்பு எனப்படுகிறது.

${\displaystyle x\cdot 1=x}$

• 0 இன் பண்பு

எந்தவொரு எண்ணையும் பூச்சியத்தால் பெருக்கக் கிடைக்கும் விடை பூச்சியமே ஆகும். இப்பண்பு பெருக்கலின் சுழியப் பண்பு அல்லது பூச்சியப் பண்பு எனப்படும்.

${\displaystyle x\cdot 0=0}$

• எதிரெண்

எந்தவொரு எண்ணையும் −1 ஆல் பெருக்கினால் அந்த எண்ணின் கூட்டல் நேர்மாறு, அதாவது அதன் எதிரெண் கிடைக்கும்.

${\displaystyle (-1)\cdot x=(-x)}$ where ${\displaystyle (-x)+x=0}$

–1 ஐ –1 ஆல் பெருக்கினால் விடை 1.

${\displaystyle (-1)\cdot (-1)=1}$

நேர்மாறு உறுப்பு

பூச்சியம் தவிர்த்த எந்தவொரு எண் x ≠ 0, க்கும் பெருக்கல் நேர்மாறு உண்டு.

x இன் பெருக்கல் நேர்மாறு: ${\displaystyle {\frac {1}{x}}}$, ${\displaystyle x\cdot \left({\frac {1}{x}}\right)=1}$.

• வரிசைக் காப்பு

நேர்ம எண்ணால் பெருக்கல், பெருக்குபடுமெண்களின் வரிசையைக் காக்கும்; மாற்றாது.

a > 0, b > c எனில் ab > ac.

எதிர்ம எண்ணால் பெருக்கல், பெருக்குபடுமெண்களின் வரிசையை எதிராக்கும்

a < 0, b > c எனில் ab < ac.

சிக்கலெண்களுக்கு வரிசைப்பண்பு கிடையாது.

எண்கள் தவிர்த்த பிற முறமைகளில் பெருக்கலுக்கு இப்பண்புகள் பொருந்தாது. எடுத்துக்காட்டாக, அணிகளின் பெருக்கலுக்குப் பரிமாற்றுத்தன்மை கிடையாது..

வெவ்வேறு வகையான எண்களின் பெருக்கல்

• முழு எண்கள்

${\displaystyle N,M\in \mathbb {Z} }$ எனில்:

${\displaystyle N\times (M)=(N)\times M=(NM)=(MN)\in \mathbb {Z} }$

${\displaystyle N\times (-M)=(-N)\times M=-(N\times M)=-(MN)=-(NM)\in \mathbb {Z} }$

${\displaystyle (-N)\times (-M)=N\times M=(NM)=(MN)\in \mathbb {Z} }$

• விகிதமுறு எண்கள்

${\displaystyle {\frac {A}{B}}\times {\frac {C}{D}}}$

${\displaystyle {\frac {A}{B}}\times {\frac {C}{D}}={\frac {(A\times C)}{(B\times D)}}}$.

• மெய்யெண்கள்

மெய்யெண்களும் அவற்றின் பெருக்கலும் விகிதமுஎண்களின் தொடர்களின் மூலம் வரையறுக்கப்படலாம்.

• சிக்கலெண்கள்

${\displaystyle z_{1}}$, ${\displaystyle z_{2}}$ இரு சிக்கலெண்கள் எனில், அவற்றின் வரிசைப்படுத்த சோடிகளின் வடிவில் பெருக்கல்:

${\displaystyle (a_{1},b_{1})}$, ${\displaystyle (a_{2},b_{2})}$

${\displaystyle z_{1}\times z_{2}}$ = ${\displaystyle (a_{1}\times a_{2}-b_{1}\times b_{2},a_{1}\times b_{2}+a_{2}\times b_{1})}$.

மேலும்,

${\displaystyle {\sqrt {-1}}=i}$

${\displaystyle z_{1}\times z_{2}=(a_{1}+b_{1}i)(a_{2}+b_{2}i)=(a_{1}\times a_{2})+(a_{1}\times b_{2}i)+(b_{1}\times a_{2}i)+(b_{1}\times b_{2}i^{2})=(a_{1}a_{2}-b_{1}b_{2})+(a_{1}b_{2}+b_{1}a_{2})i.}$

• வகுத்தல்

வகுத்தலானது வகு எண்ணின் பெருக்கல் நேர்மாறால் பெருக்குவதற்குச் சமமாகும்.

${\displaystyle {\frac {x}{y}}=x\left({\frac {1}{y}}\right)}$.

அடுக்கேற்றம்

முதன்மைக் கட்டுரை: அடுக்கேற்றம்

ஒரே எண்ணைப் பலமுறை பெருக்குவது அடுக்கேற்றம் ஆகும்.

2×2×2 = 2³

${\displaystyle a^{n}=\underbrace {a\times a\times \cdots \times a} _{n}}$

மேற்கோள்கள்

1. Khan Academy (2015-08-14), Intro to multiplication | Multiplication and division | Arithmetic | Khan Academy, பார்க்கப்பட்ட நாள் 2017-03-07
2. Khan Academy (2012-09-06), Why aren't we using the multiplication sign? | Introduction to algebra | Algebra I | Khan Academy, பார்க்கப்பட்ட நாள் 2017-03-07
3. Announcing the TI Programmable 88! (PDF). Texas Instruments. 1982. Archived from the original (PDF) on 2017-08-03. பார்க்கப்பட்ட நாள் 2017-08-03. {{cite book}}: Unknown parameter |dead-url= ignored (help)
4. Devlin, Keith (January 2011). "What Exactly is Multiplication?". Mathematical Association of America. பார்க்கப்பட்ட நாள் May 14, 2017. With multiplication you have a multiplicand (written second) multiplied by a multiplier (written first)
5. "小学校の掛け算の授業では、順序に意味があるらしい。" [In elementary school multiplication lessons, the order would appear to be meaningful] (in Japanese). September 30, 2009. பார்க்கப்பட்ட நாள் May 14, 2017.{{cite web}}: CS1 maint: unrecognized language (link)
6. Crewton Ramone. "Multiplicand and Multiplier". Crewton Ramone's House of Math. பார்க்கப்பட்ட நாள் 10 November 2015..
7. "Google book search". கூகுள் புத்தகங்கள்.
8. Fine, Henry B. (1907). The Number System of Algebra – Treated Theoretically and Historically (PDF) (2nd ed.). p. 90.

இவற்றையும் பார்க்கவும்

• கூட்டல்
• கழித்தல்
• வகுத்தல்