Пресек (теорија скупова)

За другу употребу, погледајте страницу Пресек.

У математици, пресек (ијек. пресјек; означен са ∩) два скупа и је скуп који садржи све елементе скупа који такође припадају скупу (или, еквивалентно, сви елементи скупа који такође припадају скупу ), и ниједан други елемент^[1].

Пресек два скупа

Пресек три скупа

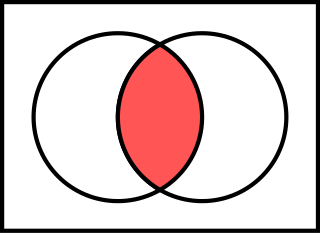
Формална дефиниција

Формална дефиниција пресека два скупа и је скуп:

${\displaystyle A\cap B=\{x:x\in A\,\land \,x\in B\}}$

тј. x ∈∩ ако и само ако

1. x ∈ и
2. x ∈ .

На пример:

• Пресек скупа {1, 2, 3} са скупом {2, 3, 4} је скуп {2, 3}.
• Број 9 није пресек скупа простих бројева {2, 3, 5, 7, 11, ...} и скупа непарних бројева {1, 3, 5, 7, 9, 11, ...}.^[2]

Уопште, може се рачунати пресек неколико скупова одједном. На пример, пресек скупова , , , и , је . Пресек скупова је асоцијативна операција па важи идентитет .

Унутар универзума може се дефинисати комплемент скупа као скуп свих елемената који нису у . Сада се пресек скупова и може записати као комплемент уније њихових комплемената, што следи из Де Морганових закона:

.

Види још

• Унија (теорија скупова)
• Подскуп

Референце

1. А. Перовић, А. Јовановић, Б. Величковић: Теорија скупова Архивирано на сајту (17. новембар 2015), Математички факултет, Београд.
2. „Пресек скупова”. Приступљено 17. 11. 2015.

Спољашње везе

• Weisstein, Eric W. "Intersection." From MathWorld-