Триангулированная категория

Триангулированная категория — это категория с «функтором сдвига» и с классом «выделенных треугольников», удовлетворяющими определённым аксиомам. Важными примерами триангулированных категорий являются производные категории абелевых категорий, а также стабильные гомотопические категории^[англ.]. Выделенные треугольники обобщают короткие точные последовательности в абелевых категориях, а также гомотопические последовательности расслоения или корасслоения в топологии.

Значительная часть гомологической алгебры была прояснена и обобщена с появлением языка триангулированных категорий, важным примером чего является теория когомологий пучков. В 1960-х годах типичным примером использования триангулированных категорий было обобщение свойств пучков на некотором пространстве X на комплексы пучков, рассматриваемые как объекты производной категории пучков на X. Со временем триангулированные категории стали рассматриваться как объекты, представляющие самостоятельный интерес. Было доказано или предположено много примеров эквивалентности между триангулированными категориями различного происхождения. Например, гипотеза гомологической зеркальной симметрии утверждает, что производная категория многообразия Калаби — Яу эквивалентна категории Фукаи^[англ.] «зеркального» симплектического многообразия.

История

Триангулированные категории были введены независимо Дитером Пуппе (1962) и Жаном-Луи Вердье^[англ.] (1963), но аксиомы Пуппе были менее полными (отсутствовала аксиома октаэдра (TR 4)).^[1][2][3][4] Пуппе мотивировался примером стабильной гомотопической категории. Для Вердье же ключевым примером были производные категории абелевых категорий, которые он определил, развивая идеи Александра Гротендика. Первыми приложениями производных категорий стали когерентная двойственность^[англ.] и двойственность Вердье^[англ.], обобщающие двойственность Пуанкаре на случай пространств с особенностями.

Определение

Функтор сдвига на аддитивной категории D — это аддитивный автоморфизм (или, как полагают некоторые авторы, автоэквивалентность) ${\displaystyle \Sigma }$ из D в D. Как правило, пишут ${\displaystyle X[n]=\Sigma ^{n}X}$ для целого n.

Треугольник (X, Y, Z, u, v, w) состоит из трёх объектов X, Y, и Z, и морфизмов ${\displaystyle u\colon X\to Y}$, ${\displaystyle v\colon Y\to Z}$ и ${\displaystyle w\colon Z\to X[1]}$. Треугольники обычно пишут в развёрнутом виде:

${\displaystyle X{\xrightarrow {{} \atop u}}Y{\xrightarrow {{} \atop v}}Z{\xrightarrow {{} \atop w}}X[1],}$

или

${\displaystyle X{\xrightarrow {{} \atop u}}Y{\xrightarrow {{} \atop v}}Z{\xrightarrow {{} \atop w}}}$

для краткости.

Триангулированная категория — это аддитивная категория D с функтором сдвига и классом треугольников, называемых выделенными треугольниками, удовлетворяющими приведённым ниже свойствам (TR 1), (TR 2), (TR 3) и (TR 4). (Эти аксиомы не являются независимыми, аксиома (TR 3) может быть выведена из остальных.^[5])

TR 1

• Для любого объекта X следующий треугольник выделен:

${\displaystyle X{\overset {\text{id}}{\to }}X\to 0\to X[1]}$

• Для любого морфизма ${\displaystyle u\colon X\to Y}$ существует объект Z (называемый конусом или кослоем морфизма u), включающийся в выделенный треугольник

${\displaystyle X{\xrightarrow {{} \atop u}}Y\to Z\to X[1]}$

Название «конус» происходит от понятия конуса^[англ.] морфизма комплексов, которое, в свою очередь, происходит от понятия конуса отображения^[англ.] в топологии. Из других аксиом следует, что выделенный треугольник (и, в частности, объект Z) определён морфизмом ${\displaystyle X\to Y}$ однозначно с точностью до изоморфизма, но не обязательно с точностью до единственного изоморфизма.^[6]

• Любой треугольник, изоморфный выделенному, выделен. Более точно, если треугольник

${\displaystyle X{\xrightarrow {{} \atop u}}Y{\xrightarrow {{} \atop v}}Z{\xrightarrow {{} \atop w}}X[1]}$

выделен, и ${\displaystyle f\colon X\to X'}$, ${\displaystyle g\colon Y\to Y',h\colon Z\to Z'}$ — изоморфизмы, то треугольник

${\displaystyle X'{\xrightarrow {guf^{-1}}}Y'{\xrightarrow {hvg^{-1}}}Z'{\xrightarrow {f[1]wh^{-1}}}X'[1]}$

также выделен.

TR 2

Если треугольник

${\displaystyle X{\xrightarrow {{} \atop u}}Y{\xrightarrow {{} \atop v}}Z{\xrightarrow {{} \atop w}}X[1]}$

выделен, то таковы и два «повёрнутых» треугольника

${\displaystyle Y{\xrightarrow {{} \atop v}}Z{\xrightarrow {{} \atop w}}X[1]{\xrightarrow {-u[1]}}Y[1]}$

и

${\displaystyle Z[-1]{\xrightarrow {-w[-1]}}X{\xrightarrow {{} \atop u}}Y{\xrightarrow {{} \atop v}}Z.\ }$

Ввиду выделенности последнего треугольника, Z[−1] называется слоем морфизма ${\displaystyle X\to Y}$.

Второй «повёрнутый» треугольник устроен более сложно, если ${\displaystyle [1]}$ и ${\displaystyle [-1]}$ — не изоморфизмы, а только взаимно обратные эквивалентности категорий, так как ${\displaystyle -w[-1]}$ в таком случае является морфизмом из ${\displaystyle Z[-1]}$ в ${\displaystyle (X[1])[-1]}$, и, чтобы получить морфизм в ${\displaystyle [X]}$, нужно взять его композицию с естественным изоморфизмом ${\displaystyle (X[1])[-1]{\xrightarrow {}}X}$. Это вызывает сложные вопросы о том, какие условия нужно наложить на естественные изоморфизмы, делающие ${\displaystyle [1]}$ и ${\displaystyle [-1]}$ парой взаимно обратных эквивалентностей. Ввиду этой проблемы, чаще всего в определении триангулированной категории предполагают, что ${\displaystyle [1]}$ и ${\displaystyle [-1]}$ являются взаимно обратными изоморфизмами.

TR 3

Пусть заданы два выделенных треугольника и отображение между первыми морфизмами в этих треугольниках. Тогда существует морфизм между третьими объектами в треугольниках, дополняющий это отображение до морфизма треугольников. Более точно, в следующей диаграмме (в которой строки являются выделенными треугольниками, а f и g — морфизмы, такие, что gu = u′f) существует морфизм h (не обязательно единственный), делающий всю диаграмму коммутативной:

TR 4: аксиома октаэдра

Пусть ${\displaystyle u\colon X\to Y}$ и ${\displaystyle v\colon Y\to Z}$ — морфизмы, рассмотрим также композицию ${\displaystyle vu\colon X\to Z}$. Каждый из этих морфизмов можно дополнить до выделенного треугольника, пользуясь аксиомой TR 1. Аксиома октаэдра утверждает, грубо говоря, что из конусов этих трёх морфизмов можно образовать выделенный треугольник, так, что «всё коммутативно».

А именно, пусть даны выделенные треугольники

${\displaystyle X{\xrightarrow {u\,}}Y{\xrightarrow {j}}Z'{\xrightarrow {k}}X[1]}$

${\displaystyle Y{\xrightarrow {v\,}}Z{\xrightarrow {l}}X'{\xrightarrow {i}}Y[1]}$

${\displaystyle X{\xrightarrow {{} \atop vu}}Z{\xrightarrow {m}}Y'{\xrightarrow {n}}X[1]}$,

тогда существует выделенный треугольник

${\displaystyle Z'\xrightarrow {f} Y'\xrightarrow {g} X'\xrightarrow {h} Z'[1],}$

такой, что

${\displaystyle l=gm,\quad k=nf,\quad h=j[1]i,\quad ig=u[1]n,\quad fj=mv.}$

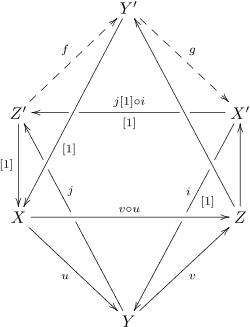
Эта аксиома называется «аксиомой октаэдра», потому что, изобразив все участвующие в ней объекты и морфизмы, можно получить скелет октаэдра, четыре из граней которого являются выделенными треугольниками. Предлагаемое ниже изложение принадлежит Вердье, и опубликовано, вместе с «диаграммой октаэдра», в книге Хартсхорна Residues and Duality^[7]. В диаграмме ниже u и v — это исходные морфизмы, а буквы со штрихами — конусы соответствующих морфизмов (таким образом, что в каждом выделенном треугольнике встречаются все три буквы X, Y, и Z). Некоторые стрелки имеют обозначение [1], чтобы показать, что они «степени 1»; например, стрелка из Z′ в X, на самом деле, представляет морфизм из Z′ в X[1]. Аксиома октаэдра утверждает существование морфизмов f и g, образующих точный треугольник, причём f и g образуют коммутативные треугольники в тех гранях, которые их содержат:

Существует также следующая полезная интуитивная интерпретация аксиомы октаэдра. В триангулированных категориях треугольники играют роль коротких точных последовательностей, поэтому целесообразно думать о штрихованных объектах как о «факторах», то есть ${\displaystyle Z'=Y/X,Y'=Z/X,X'=Z/Y}$. В этой интерпретации аксиома октаэдра эквивалентна «третьей теореме об изоморфизме»:

${\displaystyle (Z/X)/(Y/X)\cong Z/Y.}$

Если триангулированная категория — это производная категория D(A) абелевой категории A, и X, Y, Z — объекты A, рассматриваемые как комплексы, сосредоточенные в степени 0, и отображения ${\displaystyle X\to Y,Y\to Z}$ — мономорфизмы в A, то конусы этих морфизмов в D(A) на самом деле изоморфны приведённым выше факторам в A.

Свойства

Приведём некоторые простые следствия аксиом триангулированной категории D.

• Для любого выделенного треугольника

${\displaystyle X{\xrightarrow {{} \atop u}}Y{\xrightarrow {{} \atop v}}Z{\xrightarrow {{} \atop w}}X[1]}$

категории D композиция любых двух последовательных морфизмов в нём равна 0. А именно, vu = 0, wv = 0, u[1]w = 0, и т. д.^[8]

• Любой мономорфизм в D является вложением прямого слагаемого ${\displaystyle X\to X\oplus Y}$^[9], и любой эпиморфизм является проекцией вида ${\displaystyle X\oplus Y\to X}$. Соответственно, не следует говорить об «инъективности» или «сюръективности» морфизмов в триангулированной категории. Любой морфизм ${\displaystyle X\to Y}$, не являющийся изоморфизмом, имеет ненулевое «коядро» Z (в том смысле, что существует выделенный треугольник ${\displaystyle X\to Y\to Z\to X[1]}$), а также ненулевое «ядро», а именно, Z[−1].

Нефункториальность конструкции конуса

Одной из технических сложностей при работе с триангулированными категориями является «нефункториальность» конструкции конуса. Например, для любого ненулевого объекта X абелевой категории A и частичного отображения выделенных треугольников

${\displaystyle {\begin{matrix}X&\to &0&\to &X[+1]&\to \\\downarrow &&\downarrow &&&\\0&\to &X[+1]&\to &X[+1]&\to \end{matrix}}}$

в производной категории D(A), существует по крайней мере два морфизма, дополняющих эту диаграмму до коммутативной. Это тождественный морфизм и нулевой морфизм:

${\displaystyle {\begin{aligned}{\text{id}}:&X[+1]\to X[+1]\\0:&X[+1]\to X[+1].\end{aligned}}}$

Одно из возможных решений этой проблемы было предложено Гротендиком, который предлагал рассматривать не только саму производную категорию, но и производную категорию диаграмм в этой категории. Такой объект называется дериватором^[англ.]. Другими альтернативами являются стабильные ∞-категории^[англ.] и dg-категории^[англ.].

Примеры

• Векторные пространства на полем k образуют элементарную триангулированную категорию, в которой X[1] = X для всех X. Выделенные треугольники — это последовательности k-линейных отображений ${\displaystyle X\to Y\to Z\to X\to Y}$ (где одно и то же отображение ${\displaystyle X\to Y}$ встречается дважды), которые точны в X, Y и Z.
• Если A — аддитивная (например, абелева) категория, определим гомотопическую категорию^[англ.] K(A), объекты которой — цепные комплексы с членами из A, а морфизмы — классы морфизмов комплексов с точностью до гомотопии. Категория K(A) является триангулированной.^[10] Сдвинутый объект X[1] — это комплекс X, сдвинутый на один шаг влево (с дифференциалами, умноженными на −1). Выделенный треугольник в K(A) — это треугольник, изоморфный в K(A) треугольнику вида ${\displaystyle X\to Y\to {\text{cone}}(f)\to X[1]}$, ассоциированному с некоторым морфизмом комплексов ${\displaystyle f\colon X\to Y}$. (Здесь ${\displaystyle {\text{cone}}(f)}$ обозначает конус^[англ.] морфизма комплексов, см. определения в статье Производная категория.)
• Производная категория D(A) абелевой категории A является триангулированной.^[11] Она строится по категории комплексов C(A) локализацией^[англ.] по отношению к классу всех квазиизоморфизмов (то есть морфизмов комплексов ${\displaystyle f:X^{\bullet }\to Y^{\bullet }}$, индуцирующих изоморфизмы ${\displaystyle H^{n}(X^{\bullet })\to H^{n}(Y^{\bullet })}$ для всех n). Объекты D(A) при локализации не меняются, ими являются цепные комплексы. Выделенный треугольник в D(A) — это треугольник, изоморфный в D(A) треугольнику вида ${\displaystyle X\to Y\to {\text{cone}}(f)\to X[1]}$, ассоциированному с некоторым морфизмом комплексов ${\displaystyle f\colon X\to Y}$.

Основной мотивировкой для понятия производной категории является тот факт, что производные функторы на A могут быть рассматриваемы как функторы на производной категории.^[12] Некоторые естественные подкатегории D(A) также являются триангулированными категориями, например, подкатегории комплексов X, когомологические объекты ${\displaystyle H^{i}(X)}$ которых в категории A зануляются для всех достаточно малых (соответственно, достаточно больших, или достаточно больших по модулю) индексов i. Эти категории обозначаются ${\displaystyle D^{+}(A),D^{-}(A),D^{\text{b}}(A)}$, соответственно.

Когомологии в триангулированных категориях

В триангулированной категории можно определить понятие когомологий, и любая триангулированная категория имеет большой запас когомологических функторов. Когомологический функтор F из триангулированной категории D в абелеву категорию A — это такой функтор, что для любого выделенного треугольника

${\displaystyle X\to Y\to Z\to X[1]\ }$

последовательность ${\displaystyle F(X)\to F(Y)\to F(Z)}$ точна в A. Поскольку выделенный треугольник может быть продолжен до бесконечной в обоих направлениях последовательности выделенных треугольников

${\displaystyle \cdots \to Z[-1]\to X\to Y\to Z\to X[1]\to \cdots ,\ }$

когомологический функтор F определяет следующую длинную точную последовательность в A:

${\displaystyle \cdots \to F(Z[-1])\to F(X)\to F(Y)\to F(Z)\to F(X[1])\to \cdots .\ }$

Ключевым является следующий пример: для любого объекта B в триангулированной категории D функторы ${\displaystyle \operatorname {Hom} (B,{\text{-}})}$ и ${\displaystyle \operatorname {Hom} ({\text{-}},B)}$ со значениями в категории абелевых групп являются когомологическими.^[13]} (Более точно, второй из этих функторов является контравариантным, и может быть рассматриваем на категории, двойственной к D.) Таким образом, выделенный треугольник ${\displaystyle X\to Y\to Z\to X[1]}$ определяет две длинные точные последовательности абелевых групп:

${\displaystyle \cdots \to \operatorname {Hom} (B,X[i])\to \operatorname {Hom} (B,Y[i])\to \operatorname {Hom} (B,Z[i])\to \operatorname {Hom} (B,X[i+1])\to \cdots }$

и

${\displaystyle \cdots \to \operatorname {Hom} (X[i+1],B)\to \operatorname {Hom} (Z[i],B)\to \operatorname {Hom} (Y[i],B)\to \operatorname {Hom} (X[i],B)\to \cdots .}$

Для конкретных примеров триангулированных категорий эти точные последовательности дают многие важные точные последовательности в теориях когомологий пучков, когомологий групп^[англ.] и в других областях математики.

Используют также обозначение

${\displaystyle \operatorname {Ext} ^{i}(B,X)=\operatorname {Hom} (B,X[i])}$

для целого i, обобщая понятие функтора Ext в абелевой категории. В этих обозначениях первая точная последовательность может быть записана в виде

${\displaystyle \cdots \to \operatorname {Ext} ^{i}(B,X)\to \operatorname {Ext} ^{i}(B,Y)\to \operatorname {Ext} ^{i}(B,Z)\to \operatorname {Ext} ^{i+1}(B,X)\to \cdots .\ }$

Для абелевой категории A другим базовым примером когомологического функтора на производной категории D(A) является функтор, отображающий объект X в объект ${\displaystyle H^{0}(X)}$ категории A. Другими словами, точный треугольник ${\displaystyle X\to Y\to Z\to X[1]}$ в D(A) индуцирует следующую длинную точную последовательность в A:

${\displaystyle \cdots \to H^{i}(X)\to H^{i}(Y)\to H^{i}(Z)\to H^{i+1}(X)\to \cdots ,}$

так как ${\displaystyle H^{0}(X[i])\cong H^{i}(X)}$.

Точные функторы и эквивалентности

Точный функтор (или триангулированный функтор) из триангулированной категории D в триангулированную категорию E — это аддитивный функтор ${\displaystyle F\colon D\to E}$, который, грубо говоря, коммутирует со сдвигами и переводит выделенные треугольники в выделенные.^[14]

Более строго, точный функтор снабжён естественным изоморфизмом ${\displaystyle \eta \colon F\Sigma \to \Sigma F}$ (где первое ${\displaystyle \Sigma }$ обозначает функтор сдвига в D, а второе — функтор сдвига в E), такой, что для любого выделенного треугольника

${\displaystyle X{\xrightarrow {{} \atop u}}Y{\xrightarrow {{} \atop v}}Z{\xrightarrow {{} \atop w}}X[1]}$

в категории D, треугольник

${\displaystyle F(X){\xrightarrow {F(u)}}F(Y){\xrightarrow {F(v)}}F(Z){\xrightarrow {\eta _{X}F(w)}}F(X)[1]}$

является выделенным в E.

Эквивалентность триангулированных категорий — это точный функтор ${\displaystyle F\colon D\to E}$, который является эквивалентностью категорий. В такой ситуации существует точный функтор ${\displaystyle G\colon E\to D}$, такой, что FG и GF естественно изоморфны тождественным функторам в соответствующих категориях.

Примечания

1. Puppe, 1962.
2. Puppe, 1967.
3. Verdier, 1977.
4. Verdier, 1996.
5. J. Peter May, The axioms for triangulated categories Архивная копия от 14 июня 2024 на Wayback Machine.
6. Weibel, 1994, Remark 10.2.2.
7. Hartshorne, 1966.
8. Weibel, 1994, Exercise 10.2.1.
9. Гельфанд, Манин, 1988, Exercise IV.1.1.
10. Kashiwara, Schapira, 2006, Theorem 11.2.6.
11. Гельфанд, Манин, 1988, Глава IV, §2.
12. Гельфанд, Манин, 1988, Глава III, §6.
13. Гельфанд, Манин, 1988, Глава IV, §1, Предложение 3 и п. 6.
14. Weibel, 1994, Definition 10.2.6..

Литература

• Гельфанд С. И., Манин Ю. И. Методы гомологической алгебры. — М.: Наука, 1988. — Т. 1. Введение в теорию когомологий и производные категории. — 416 с. — ISBN 5-02-014414-2.
• Kashiwara, Masaki; Schapira, Pierre. Categories and Sheaves. — Berlin, New York: Springer-Verlag, 2006. — (Grundlehren der mathematischen Wissenschaften). — ISBN 978-3-540-27949-5.
• Hartshorne, Robin. Chapter I. The Derived Category // Residues and duality. — Springer-Verlag, 1966. — P. 20–48. — (Lecture Notes in Mathematics 20). — ISBN 978-3-540-03603-6. — doi:10.1007/BFb0080482.
• Puppe, Dieter. On the formal structure of stable homotopy theory // Colloquium on algebraic topology. — Aarhus Universitet Matematisk Institute, 1962. — P. 65–71.
• Puppe, Dieter. Stabile Homotopietheorie. I. // Mathematische Annalen. — 1967. — Т. 169, вып. 2. — P. 243–274. — doi:10.1007/BF01362348.
• Verdier, Jean-Louis. Catégories dérivées: quelques résultats (état 0) // Cohomologie étale (SGA 4 1/2). — Springer, 1977. — P. 262–311. — (Lecture Notes in Mathematics). — ISBN 978-3-540-08066-4. — doi:10.1007/BFb0091525.
• Verdier, Jean-Louis. Des Catégories Dérivées des Catégories Abéliennes (фр.) // Astérisque. — Paris: Société Mathématique de France, 1996. — Vol. 239. — ISSN 0303-1179.
• Weibel, Charles A. An introduction to homological algebra. — Cambridge University Press, 1994. — Vol. 38. — (Cambridge Studies in Advanced Mathematics). — ISBN 978-0-521-55987-4.