Многогранник, многоугольник или мозаика является изотоксальным или рёберно транзитивным, если его симметрии действуют транзитивно на его рёбрах. Неформально это означает, что имеется только один вид рёбер у объекта — если даны два ребра, существует параллельный перенос, вращение и/или зеркальное отражение, переводящее одно ребро в другое, не меняя область, занимаемую объектом.
Термин изотоксальный происходит от греческого τοξον, означающего дуга.
Изотоксальные многоугольники
Изотоксальный многоугольник всегда является равносторонним, но не все равносторонние многоугольники изотоксальны. Двойственные изотоксальным многоугольникам являются изогональными многоугольниками.
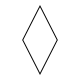
В общем случае изотоксальный 2n-угольник будет иметь Dn (*nn) диэдральную симметрию. Ромб является рёберно транзитивным многоугольником с симметрией D2 (*22).
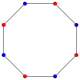
Все правильные многоугольники (правильный треугольник, квадрат, и т. д.) изотоксальны, имея удвоенный минимальный порядок симметрии — правильный n-угольник имеет Dn (*nn) диэдральную симметрию. Правильный 2n-угольник является вершинно транзитивным многоугольником и его вершины могут быть помечены поочерёдно двумя цветами, что удаляет осевую симметрию через середину рёбер.
| D2 (*22) | D3 (*33) | D4 (*44) | D5 (*55) | |||||
|---|---|---|---|---|---|---|---|---|
| Ромб | Равносторонний треугольник | Вогнутый шестиугольник | Самопересекающийся шестиугольник | Выпуклый восьмиугольник | Правильный пятиугольник | Самопересекающаяся (правильная) пентаграмма | Самопересекающаяся декаграмма | |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Рёберно-транзитивные многогранники и мозаики
Правильные многогранники являются изоэдральными (гране транзитивными), изогональными (вершинно транзитивными) и изотоксальными (рёберно транзитивными). Квазиправильные многогранники являются изогональными и изотоксальными, но не изоэдральными. Их двойственные многогранники изоэдральны и изотоксальны, но не изогональны.
| Квазиправильный многогранник |
Квазиправильный двойственный многогранник |
Квазиправильный звёздчатый многогранник |
Квазиправильный двойственный звёздчатый многогранник |
Квазиправильная мозаика |
Квазиправильная двойственная мозаика |
|---|---|---|---|---|---|
 Кубооктаэдр является изогональным и изотоксальным многогранником |
 Ромбододекаэдр является изоэдральным и изотоксальным многогранником |
 Большой икосододекаэдр является изогональным и изотоксальным звёздчатым многогранником |
 Большой ромбический тридцатигранник |
 Тришестиугольная мозаика является изогональной и изотоксальной мозаикой |
 Ромбическая мозаика является изоэдральной и изотоксальной мозаикой с симметрией p6m (*632). |
Не любой многогранник или 2-мерная мозаика, состоящие из правильных многоугольников, изотоксален. Например, усечённый икосаэдр (знакомый нам по футбольному мячу) имеет два типа рёбер — шестиугольник-шестиугольник и шестиугольник-пятиугольник и нет возможности симметрией перевести ребро шестиугольник-шестиугольник в шестиугольник-пятиугольник.
Изотоксальный многоугольник имеет те же самые диэдральные углы для всех рёбер.
Существует девять выпуклых рёберно транзитивных многогранников, образованных из правильных многогранников, 8, образованных из многогранников Кеплера — Пуансо, и ещё шесть являются квазиправильными звёздчатыми многогранниками (3 | p q) и их двойственными.
Существует 5 многоугольных рёберно транзитивных мозаик на евклидовой плоскости и бесконечно много на гиперболической плоскости, включая построения Уитхофф из правильных гиперболических мозаик {p, q} и неправильных (p q r) групп.
См. также
Примечания
Литература
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.