Тришестиугольная мозаика

Тришестиугольная мозаика — одна из 11 однородных мозаик на евклидовой плоскости из правильных многоугольников^[1]. Мозаика состоит из правильных треугольников и правильных шестиугольников, расположенных так, что каждый шестиугольник окружён треугольниками, и наоборот. Название мозаики вызвано тем фактом, что она комбинирует правильную шестиугольную мозаику и правильную треугольную мозаику. Два шестиугольника и два треугольника чередуются вокруг каждой вершины, а рёбра образуют бесконечную конфигурацию прямых. Двойственная мозаика — ромбическая^[2].

Тришестиугольная мозаика
Тип	полуправильная мозаика
Конфигурация вершины	(3.6)2
Символ Шлефли	r{6,3} или ${\displaystyle {\begin{Bmatrix}6\\3\end{Bmatrix}}}$ h2{6,3}
Символ Витхоффа[англ.]	2 | 6 3 3 3 | 3
Диаграмма Коксетера — Дынкина	=
Симметрии	p6m[англ.], [6,3], (*632)
Симметрии вращения	p6[англ.], [6,3]+, (632) p3, [3[3]]+, (333)
Обозначение Бауэрса	That
Двойственные соты	ромбическая мозаика
Свойства	вершинно транзитивная рёберно транзитивная

Мозаика и её место в классификации однородных мозаик были приведены Иоганном Кеплером ещё в 1619 в его книге Harmonices Mundi^[3]. Узор давно использовался в японском лозоплетении, где он назывался кагомэ. Японский термин для этого узора был позаимствован физиками, где он получил название решётка кагомэ. Узор встречается в кристаллических структурах некоторых минералов. Конвей использовал название hexadeltille (шести-дельта-мозаика), скомбинировав части слов hex-/deltа/tille^[4].

Кагомэ

Японская корзина с узором кагомэ

Кагомэ (яп. 籠目) — это традиционный японский узор плетения бамбука. Название состоит из слов каго (корзина) и мэ (глаз), последнее относится к отверстиям в бамбуковой корзине.

Детальный вид плетения кагомэ

Кагомэ представляет собой переплетённую конфигурацию прутьев, образующая узор тришестиугольной мозаики. Плетение даёт кагоме симметрию хиральной группы обоев^[англ.], группы p6.

Решётка кагомэ

Термин решётка кагомэ ввёл японский физик, иностранный член РАН^[5] Кодзи Фусими^[англ.]. Термин впервые появился в статье 1951, написанной Исиро Сёдзи под руководством Фусими^[6]. Решётка кагомэ в этом смысле состоит из вершин и рёбер тришестиугольной мозаики. Вопреки названию, эти пересечения не образуют математическую решётку.

Связанная трёхмерная структура, образованная вершинами и рёбрами четвертькубических сот^[англ.], заполняющих пространство правильными тетраэдрами и усечёнными тетраэдрами, называется гиперрешёткой кагомэ ^[7]. Она представляется вершинами и рёбрами четвертькубических сот, заполняющих пространство тетраэдрами и усечёнными тетраэдрами. Структура содержит четыре множества параллельных плоскостей, и каждая плоскость является двумерной решёткой кагомэ. Другое представление в трёхмерном пространстве имеет параллельные уровни двумерных решёток и называется орторомбическая решётка кагомэ^[7]. Тришестиугольные призматические соты представляют рёбра и вершины этой решётки.

Некоторые минералы, а именно ярозит и гербертсмитит, содержат двумерные решётки или трёхмерные решётки кагомэ, образованные из атомов в кристаллической структуре. Эти минералы показывают физические свойства, связанные с магнитами с геометрической фрустрацией. Например, распределение спинов магнитных ионов в Co₃V₂O₈ располагается в виде решётки кагомэ и показывает удивительное магнитное поведение при низких температурах^[8]. Термин имеет сейчас широкое распространение в научной литературе, особенно в теоретическом изучении магнитных свойств теоретической решётки кагомэ.

Симметрия

Треугольные 30-60-90 фундаментальные области симметрии p6m (*632)

Тришестиугольная мозаика имеет символ Шлефли r{6,3} и диаграмму Коксетера — Дынкина , символизирующие факт, что мозаика является полноусечённой шестиугольной мозаикой, {6,3}. Её симметрии можно описать группой обоев p6mm, (*632)^[9]. Мозаика может быть получена построением Витхоффа из фундаментальных областей отражений этой группы. Тришестиугольная мозаика является квазиправильной мозаикой, чередующей два типа многоугольников и имеющей конфигурацию вершины (3.6)². Мозаика является также однородной мозаикой, одной из восьми, полученных из правильной шестиугольной мозаики.

Однородные раскраски

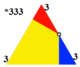
Существует две различные однородные раскраски тришестиугольной мозаики. Эти две раскраски, если указать индексы цветов для 4 граней вокруг вершины (3.6.3.6), имеют наборы индексов 1212 и 1232^[10]. Вторая раскраска называется скошенной шестиугольной мозаикой, h₂{6,3}, с двумя цветами треугольников из симметрии (*333) группы обоев p3m1.

Симметрия	p6m, (*632)	p3m, (*333)
Раскраска
фундаментальная область
символ Витхоффа[англ.]	2 | 6 3	3 3 | 3
диаграмма Коксетера — Дынкина		=
символ Шлефли	r{6,3}	r{3[3]} = h2{6,3}

Топологически эквивалентные мозаики

Тришестиугольная мозаика может быть геометрически искривлена в топологически эквивалентные мозаики с меньшей степенью симметрии^[10]. В этих вариантах мозаики рёбра не обязательно являются отрезками (могут быть кривыми).

p3m1, (*333)	p3, (333)	p31m, (3*3)

Связанные квазирегулярные мозаики

Тришестиугольная мозаика присутствует в последовательности симметрий квазирегулярных мозаик с конфигурациями вершин (3.n)², которая начинается с мозаик на сфере, идёт к евклидовой плоскости и переходит в гипеболическую плоскость. С орбифолдной нотацией^[англ.] симметрии *n32 все эти мозаики создаются построением Витхоффа с фундаментальной областью симметрии и генераторной точкой в вершине области с прямым углом^[11][12].

*n32 орбифолдные симметрии квазирегулярных мозаик: (3.n)²

Построение	Сферическая			Евклидова	Гиперболическая
	*332	*432	*532	*632	*732	*832...	*∞32
Квазирегулярные фигуры
Вершина	(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2

Связанные правильные комплексные бесконечноугольники

Существует 2 правильных комплексных бесконечноугольника, имеющие те же вершины, что и тришестиугольная мозаика. Правильные комплексные бесконечноугольники имеют вершины и рёбра, при этом рёбра могут иметь 2 и более вершин. Правильные бесконечноугольники (апейрогоны) p{q}r имеют ограничивающее равенство: 1/p + 2/q + 1/r = 1. Рёбра имеют p вершин, расположенных как у правильного многоугольника, а вершинные фигуры r-угольны^[13].

Первый бесконечноугольник состоит из треугольных рёбер, по два треугольника вокруг каждой вершины, второй имеет шестиугольные рёбра, по два шестиугольника вокруг каждой вершины.

3{12}2 or	6{6}2 or

См. также

• Порог перколяции^[англ.]
• Звезда Давида
• Тришестиугольные призматические соты