Пересечение множеств

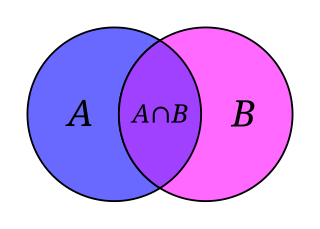
Пересече́ние мно́жеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам. Пересечение двух множеств ${\displaystyle A}$ и ${\displaystyle B}$ обычно обозначается ${\displaystyle A\cap B}$, но в редких случаях может обозначаться ${\displaystyle AB}$^[1].

Пересечение ${\displaystyle A}$ и ${\displaystyle B}$

Определение

Пересечение двух множеств

Пусть даны множества ${\displaystyle A}$ и ${\displaystyle B}$. Тогда их пересечением называется множество

${\displaystyle A\cap B=\{x\mid x\in A\wedge x\in B\}.}$

Пересечение семейства множеств

Пусть дано семейство множеств ${\displaystyle \{M_{\alpha }\}_{\alpha \in A}.}$ Тогда его пересечением называется множество, состоящее из элементов, которые входят во все множества семейства:

${\displaystyle \bigcap \limits _{\alpha \in A}M_{\alpha }=\{x\mid \forall \alpha \in A,\;x\in M_{\alpha }\}.}$

Свойства

• Пересечение множеств является бинарной операцией на произвольном булеане ${\displaystyle 2^{X}}$;
• Операция пересечения множеств коммутативна

  ${\displaystyle A\cap B=B\cap A;}$

• Операция пересечения множеств ассоциативна:

  ${\displaystyle (A\cap B)\cap C=A\cap (B\cap C);}$

• Операция пересечения множеств дистрибутивна относительно операции объединения:^[2]

  ${\displaystyle \left(\bigcup _{k}A_{k}\right)\cap B=\bigcup _{k}\left(A_{k}\cap B\right)}$

• Универсальное множество ${\displaystyle U}$ является нейтральным элементом операции пересечения множеств:

  ${\displaystyle A\cap U=A;}$

• Операция пересечения множеств идемпотентна:

  ${\displaystyle A\cap A=A;}$

• Если ${\displaystyle \varnothing }$ — пустое множество, то

  ${\displaystyle A\cap \varnothing =\varnothing .}$

Пример

Пусть ${\displaystyle A=\{1,\;2,\;3,\;4\}}$, ${\displaystyle B=\{3,\;4,\;5,\;6,\;7\}}$. Тогда

${\displaystyle A\cap B=\{3,\;4\}.}$