Retas paralelas

Segundo a geometria euclidiana, duas retas distintas de um plano são paralelas (símbolo ∥), quando não têm um ponto comum.^[1][2]

Proposição 27

Retas paralelas

Feixe de retas paralelas

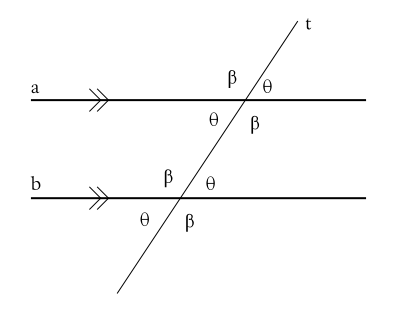
A proposição 27, de Euclides, dá uma condição suficiente para duas linhas serem paralelas: se uma reta corta outras duas retas de forma que os ângulos alternados sejam iguais, então estas outras duas retas são paralelas^[3] A demonstração é por redução ao absurdo: supondo-se que elas não sejam paralelas, forma-se um triângulo em que um ângulo exterior é igual a um ângulo interior oposto.^[3]

A partir de três retas paralelas tem-se um feixe de retas paralelas.

Geometria Analitica

Em geometria analítica se duas retas r e s têm as seguintes equações reduzidas

• ${\displaystyle r:y=ax+b}$
• ${\displaystyle s:y=a'x+b'}$

elas serão paralelas se e somente se os coeficientes angulares (a e a') forem iguais. Caso contrário elas serão concorrentes.^{[4][notas 1]}

Notas

1. Duas retas ambas horizontais ou verticais serão sempre paralelas sendo uma exceção à regra dos coeficientes angulares.

Referências

1. Putnoki, José Carlos - Elementos de Geometria e desenho geométrico. Vol. 1. Ed. Scipione, São Paulo, 1989. p. 79.
2. Euclides, Os Elementos, Livro I, Definição 23 [em linha]
3. Euclides, Os Elementos, Livro I, Proposição 27 [em linha]
4. RIGONATTO, Marcelo. «Retas Paralelas». Brasil Escola. Consultado em 1 de junho de 2018