Ogiva

 Nota: Para outros significados, veja Ogiva (desambiguação).

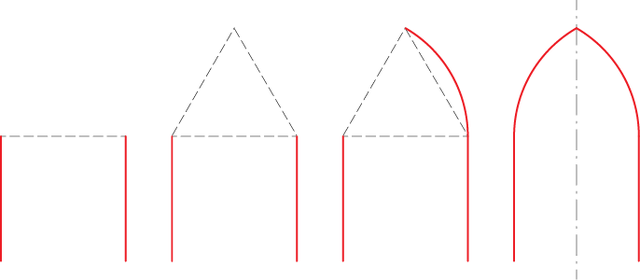
A ogiva é uma forma determinada por dois arcos, comumente simétricos, que se cortam em ângulo. A palavra ogiva começou a ser usada no século XVIII para designar um arco que define um ângulo curvilíneo.^[2] A ogiva geométrica admite variações chamadas de arco ogival, arco de ogiva e, até mesmo, arco quebrado^{[nota 1]}, nas quais os centros dos arcos (O1 e O2) podem estar dentro ou fora dos limites da forma. A ogiva também pode ser um elemento tridimensional, oriundo da revolução da curva geométrica sobre o eixo de simetria.

Ogiva simétrica, baseada num triângulo equilátero^[1]

Diferentes ogivas: A (centros dentro da base da ogiva)^{[nota 3]}, B (centros nos pés da ogiva - simétrica equilátera) e C (nesta construção específica, a altura e a largura são iguais e os centros encontram-se fora da base da ogiva).^{[nota 2][1]}

Ogiva lanceolada

Esta ogiva é formada por dois arcos de circunferência, cujos centros se encontram afastados e fora da área da ogiva, na seguinte relação: a altura do arco ogival é igual a 0,979 vezes a sua largura.^[1]

Ogiva lanceolada, cuja altura é ligeiramente menor do que a largura^[1]

Aplicações

• Na arquitetura esse tipo de figura caracteriza o estilo gótico, podendo formar um ângulo mais ou menos agudo na parte superior.^[3]
• Na engenharia trata-se da parte afilada de um corpo cilíndrico, geralmente destinado a ser lançado, como, por exemplo, um projétil, um foguete entre outros.^[3]
• Em balística a ogiva é uma superfície de revolução tridimensional, que é parte de um projétil que contém os elementos potencialmente causadores de dano, sejam eles sistemas nucleares, termonucleares, explosivos, químicos ou biológicos.

Arco ogival aplicado na arquitetura.

Notas

^{[nota 1] ^} A altura do arco (flecha) é maior do que a sua largura (luz).

^{[nota 2] ^} Se a distância entre 01 e 02 for maior do que a do exemplo C, então o arco ogival será do tipo arco quebrado, pois a altura (flecha) será maior do que a sua largura (luz).

^{[nota 3] ^} Se 01 coincidir com 02 (excentricidade zero), têm-se o arco romano, e a figura deixa de ser uma ogiva.

Referências

1. Braga, Theodoro - Desenho linear geométrico. Ed. Cone, São Paulo: 1997; p. 175.
2. Braga, Theodoro - Desenho linear geométrico. Ed. Cone, São Paulo: 1997; p. 223.
3. Dicionário Eletrônico Houaiss, 3.0, junho de 2009.