Top Qs
Linha do tempo
Chat
Contexto
Constante de Euler-Mascheroni
uma constante matemática; o limite da diferença entre a série harmônica e o logaritmo natural Da Wikipédia, a enciclopédia livre
Remove ads
Remove ads
A constante de Euler-Mascheroni (também chamada de constante de Euler) é uma constante matemática, geralmente denotada pela letra grega gama (γ) , com múltiplas utilizações em Teoria dos números. Ela é definida como o limite da diferença entre a série harmônica e o logaritmo natural, denotado aqui por log:
| Este artigo utiliza notação matemática técnica para logaritmos. Todas as instâncias de log(x) sem uma base subscrita devem ser interpretadas como um logaritmo natural, usualmente denotado como ln(x) ou loge(x). |

Aqui, ⌊·⌋ representa a função piso.
O valor numérico da constante de Euler-Mascheroni, com 50 casas após a vírgula, é:[1]
Problema de matemática em aberto:
A constante de Euler-Mascheroni é irracional? Se for, é transcendente?
Remove ads
História
A constante foi definida pela primeira vez pelo matemático suíço Leonhard Euler no artigo De Progressionibus harmonicus observationes, publicado em 1735. Euler usou a notação C para a constante, e inicialmente calculou seu valor até 6 casas decimais. Em 1761 Euler estendeu seus cálculos, publicando um valor com 16 casas decimais. Em 1790 o matemático italiano Lorenzo Mascheroni introduziu a notação γ para a constante, e tentou estender o cálculo de Euler ainda mais, a 32 casas decimais, apesar de cálculos subseqüentes terem mostrado que ele cometera erros na 20°, 22° e 32 casas decimais. (Do 20° dígito, Mascheroni calculou 1811209008239.)
Não se sabe se a constante de Euler-Mascheroni é ou não um número racional. No entanto, análises mostram que se γ for racional, seu denominador tem mais do que 10242080 dígitos (Havil, page 97).
Remove ads
Convergência
Resumir
Perspectiva
Como podemos escrever:
Como
Mostremos que a série converge uniformemente, para tal usamos a estimativa:
Essa última expressão corresponde à
Que é a série telescópica Dessa forma,
Remove ads
Propriedades
Resumir
Perspectiva
O número não foi provado que seja algébrico ou transcendente, e , nem sequer se conhece se é irracional ou não.[2] A análise de frações contínuas revela que se é racional, seu denominador deve ser da ordem de .[3] Devido ao fato de estar presente em um grande número de equações e relações, a racionalidade ou irracionalidade de está os problemas abertos mais importantes da Matemática.
A seguir estão apresentadas as relações mais importantes de com funções, séries e integrais.
Representação Original (Euler)
Foi descoberta em 1734, por Euler, representando como uma série infinita da seguinte forma:
Relação com a Função Gama
Se tomarmos a função gama, derivando-a e analisando-a em 1, obtemos -. O mesmo comportamento é observado se analisarmos a função digama em 1, ou seja:
também como o limite:
O limite relacionado com a função beta ( expressa em termos da função gama) é:
e como função beta:
Relação com a Função Zeta de Riemann
pode ser expresso por uma soma infinita, cujos termos envolvem a Função Zeta de Riemann para números positivos da seguinte forma:
Outras séries relacionadas com a função zeta são:
O termo erro na última equação está decrescendo rapidamente em função de n . Como resultado, a fórmula se mostra bastante eficiente para cálculo de grande quantidade de dígitos da constante com extrema precisão.
Outro limite interessante relacionado com a Constante de Euler-Mascheroni e a função zeta é o limite assimétrico:
Representação com Integrais
é igual ao valor de um número determinado de integrais definidas:
Dentre as integrais definidas nas quais aparece a constante estão:
Uma expressão em que se expressa como uma integral dupla,[4] com sua série equivalente é:
Representação com Séries
Além da série original de Euler, são conhecidas outras séries,em que se inclui:
encontrada por Nielsen em 1897.
Em 1912, Vacca encontrou a seguinte série relacionada a :
onde [ ] é a função piso e é o logaritmo de base 2 ;
Em 1926, Vacca encontrou outra série similar a anterior:
que também pode ser escrita como:
As últimas 2 séries podem ser obtidas através da manipulação da Integral de Catalão( ver Sondow e Zudilin)
Representação em forma de fração contínua
A representação de em termos de fração contínua é:
mais precisamente:
Remove ads
Referências
- Courant, R. Introducción al Cálculo y al Análisis Matemático. México: Editorial Limusa
- Havil (2003). Título ainda não informado (favor adicionar). [S.l.: s.n.] p. 97
- Krämer, Stefan. «Euler's Constant γ=0.577... Its Mathematics and History»
- Euler, Leonhard, De progressionibus harmonicis observationes. Commentarii academiae scientiarum Petropolitanae 7, 1740, pp. 150–161. Reprinted in Opera Omnia: Series 1, Volume 14, pp. 87 – 100
- Borwein, Jonathan M., David M. Bradley, Richard E. Crandall (2000). Computational. «Strategies for the Riemann Zeta Function» (PDF). Journal of Computational and Applied Mathematics. 121. p.11 Derives γ as sums over Riemann zeta functions. (en inglés)
- Havil, Julian (2003). Gamma: Exploring Euler's Constant. [S.l.]: Princeton University Press. ISBN 0-691-09983-9 (en inglés)
- Donald Knuth (1997) The Art of Computer Programming, Vol. 1, 3rd ed. Addison-Wesley. ISBN 0-201-89683-4 (en inglés)
- Krämer, Stefan (2005) Die Eulersche Konstante γ und verwandte Zahlen. Diplomarbeit, Universität Göttingen. (alemán)
- Sondow, Jonathan (1998) "An antisymmetric formula for Euler's constant," Mathematics Magazine 71: 219-220. (en inglés)
- ------ (2002) Gourdon, Xavier, and Sebah, P."Collection of formulas for Euler's constant, γ." (en inglés)
- ------ (2002) "A hypergeometric approach, via linear forms involving logarithms, to irrationality criteria for Euler's constant." With an Appendix by Sergey Zlobin. (en inglés)
- ------ (2003) "An infinite product for eγ via hypergeometric formulas for Euler's constant, γ." (en inglés)
- ------ (2003a) ""Criteria for irrationality of Euler's constant," Proceedings of the American Mathematical Society 131: 3335-3344. (en inglés)
- ------ (2005) "Double integrals for Euler's constant and ln 4/π and an analog of Hadjicostas's formula," American Mathematical Monthly 112: 61-65. (en inglés)
- ------ (2005) "New Vacca-type rational series for Euler's constant and its 'alternating' analog ln 4/π." (en inglés)
- ------ and Wadim Zudilin (2006), "Euler's constant, q-logarithms, and formulas of Ramanujan and Gosper," Ramanujan Journal 12: 225-244.
Remove ads
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
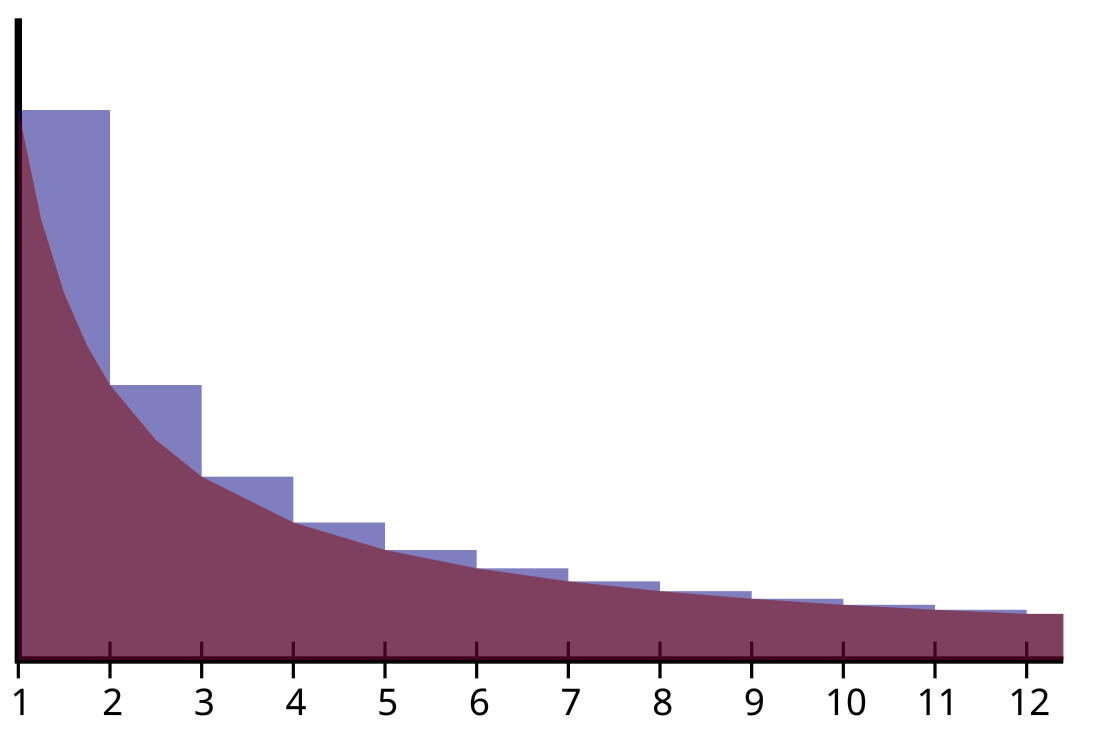
![{\displaystyle {\begin{aligned}\gamma &=\lim _{n\to \infty }\left(-\log n+\sum _{k=1}^{n}{\frac {1}{k}}\right)\\[5px]&=\int _{1}^{\infty }\left(-{\frac {1}{x}}+{\frac {1}{\lfloor x\rfloor }}\right)\,dx.\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c56b1749b8d9029307ae1a6a0657183622fc78a8)
![{\displaystyle {\begin{aligned}\ln n&=[\ln n-\ln(n-1)]+[\ln(n-1)-\ln(n-2)]+\ldots +[\ln 2-\ln 1]+\ln(1)\\&=\sum _{k=2}^{n}\,[\ln k-\ln(k-1)]\end{aligned}}\,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/57678f174b1dab86d339c62d0edac623d16fec63)








![{\displaystyle \gamma =\sum _{k=1}^{\infty }\left[{\frac {1}{k}}-\ln \left(1+{\frac {1}{k}}\right)\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7176d3dc104a5ef96f1039306f330096dde13ccd)

![{\displaystyle \gamma =\lim _{n\to \infty }\left[n-\Gamma \left({\frac {1}{n}}\right)\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8133a08de9e662e2e471e80336cdbdc1b6fda91f)
![{\displaystyle -\gamma =\lim _{n\to \infty }\left[{\frac {\Gamma ({\frac {1}{n}})\Gamma (n+1)\,n^{1+{1 \over n}}}{\Gamma (2+n+{\frac {1}{n}})}}-{\frac {n^{2}}{n+1}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3ee70d47fdc22f162f27e3c27f416b1d200b0257)
![{\displaystyle -\gamma =\lim _{n\to \infty }\left[n^{2+{1 \over n}}\,\mathrm {B} \left(1+{\frac {1}{n}},\,n+1\right)-{\frac {n^{2}}{n+1}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/205e15b1339f10927ae48dd652b32a01d4553db4)

![{\displaystyle \gamma ={\frac {3}{2}}-\log 2-\sum _{k=2}^{\infty }(-1)^{k}\,{\frac {k-1}{k}}[\zeta (k)-1]=\lim _{n\to \infty }\left[{\frac {2\,n-1}{2\,n}}-\log \,n+\sum _{k=2}^{n}\left({\frac {1}{k}}-{\frac {\zeta (1-k)}{n^{k}}}\right)\right]=\lim _{n\to \infty }\left[{\frac {2^{n}}{e^{2^{n}}}}\sum _{k=0}^{\infty }{\frac {2^{k\,n}}{(k+1)!}}\sum _{t=0}^{k}{\frac {1}{t+1}}-n\,\log 2+{\mathcal {O}}\left({\frac {1}{2^{n}\,e^{2^{n}}}}\right)\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/433f66c25c8312fa2ffb4ab909e6d1929c6ce057)












![{\displaystyle \gamma =[0;1,1,2,1,2,1,4,3,13,5,1,1,8,1,2,4,1,1,40,...]\,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4bd27ebd870468dbb92cf355e1d9525467520096)