Top Qs
Linha do tempo
Chat
Contexto
Begriffsschrift
sistema formal desenvolvido por Gottlob Frege, marcando o nascimento da lógica moderna Da Wikipédia, a enciclopédia livre
Remove ads
Remove ads
Begriffsschrift (Traduzido grosseiramente do alemão para "ideografia") é um livro de lógica feito por Gottlob Frege, publicado em 1879, e o sistema formal estabelecido neste livro. Este é geralmente considerado a obra que marca o nascimento da lógica moderna.
Esta página ou se(c)ção precisa ser formatada para o padrão wiki. (Junho de 2022) |

Begriffsschrift é usualmente traduzido como escrita conceitual ou notação conceitual ou conceitografia; o título completo deste livro o identifica como "uma fórmula de linguagem, modelada a partir da aritmética, para o pensamento puro." A motivação de Frege para desenvolver esta abordagem formal para a lógica era similar à motivação de Gottfried Leibniz para seu cálculo raciocinador (apesar disto, em seu "prefácio", Frege claramente nega que ele atingiu este objetivo, e também que seu principal objetivo poderia ser a construção de uma linguagem ideal como a de Leibniz, o que Frege declara ser uma tarefa bastante difícil e idealista, entretanto, não impossível). Frege passou a empregar seu cálculo lógico em pesquisas sobre os fundamentos da matemática, realizadas durante o quarto de século seguinte.
Remove ads
A notação e o sistema
Resumir
Perspectiva
O cálculo contém o primeiro aparecimento de variáveis quantificadas, e é essencialmente uma lógica de segunda ordem clássica bivalente com identidade, embora apresentado usando uma notação altamente idiossincrática bidimensional: conectivos e quantificadores são escritos usando uma linha conectando fórmulas, em vez dos símbolos: ¬, ∧ e ∀ em uso hoje em dia. Por exemplo, que o julgamento implica materialmente no julgamento , i.e. é escrita como ![]() .
.
No primeiro capítulo, Frege define ideias básicas e a notação, como proposição ("julgamento"), o quantificador universal(“a generalidade”), o condicional, negação e o “sinal de identidade de conteúdo” (o que ele usou para indicar tanto equivalência material quanto identidade própria); no segundo capítulo ele declara nove proposições formalizadas como axiomas.
No capítulo 1, §5, Frege define o condicional da seguinte maneira:
- "Sejam A e B referentes aos conteúdos deriváveis, então as quatro possibilidades são:
- A é afirmado, B é afirmado;
- A é afirmado, B é negado;
- A é negado, B é afirmado;
- A é negado, B é negado.
Seja
significa que a terceira destas possibilidades não é obtida, porém as outras três sim. Então se negarmos  ,isto significa que a terceira possibilidade é válida, ou seja, negamos A e afirmamos B."
,isto significa que a terceira possibilidade é válida, ou seja, negamos A e afirmamos B."
Remove ads
O cálculo na obra de Frege
Resumir
Perspectiva
Frege declarou nove de suas proposições como axiomas, e as justifica argumentando informalmente que, dados seus significados desejados, elas expressam verdades auto evidentes. Re-expressos na notação contemporânea, esses axiomas são:
Estas são as proposições 1, 2, 8, 28, 31, 41, 52, 54, e 58 em o Begriffschrifft. (1)-(3) regem implicação material, (4)-(6) negação, (7) e (8) identidade, e (9) o quantificador universal. (7) expressa a indiscernibilidade de idênticos de Leibniz, e (8) afirma que identidade é uma relação reflexiva.
Todas as outras proposições são deduzidas de (1)-(9) usando-se qualquer uma das regras de inferência abaixo:
- Modus ponens permite-nos inferir a partir de e ;
- A regra da generalização nos permite inferir a partir de se x não ocorre em P;
- A regra da substituição, cuja Frege não declara explicitamente. Esta regra é mais difícil de articular precisamente do que as duas regras anteriores, e Frege usa isto de maneiras que não são obviamente legítimas.
Os principais resultados do terceiro capítulo, intitulado "Partes de uma teoria geral de séries", dizem respeito ao que hoje chamamos de ancestral de uma relação R. "a é um R-antepassado de b" é escrito como "aR*b".
Frege aplicou o resultado de o Begriffsschrifft, , incluindo aqueles no ancestral de uma relação, na sua obra posterior The Foundations of Arithmetic. Assim, se tomarmos xRy como sendo uma relação y=x+1, então 0R*y é o predicado "y é um número natural." (133) diz que se x, y, e z são números naturais, então uma das seguintes relações é mantida: x<y, x=y, ou y<x. Esta é a então chamada "lei da tricotomia".
Remove ads
Influência em outros trabalhos
Resumir
Perspectiva
Para um cuidadoso estudo recente de como o Begriffsschrift foi avaliado na literatura matemática Alemã, veja Vilko (1998). Alguns avaliadores, especialmente Ernst Schröder, estavam favoráveis. Todo trabalho na lógica formal subsequente ao Begriffsschrift deve-se a esta obra, porque esta lógica de segunda ordem foi a primeira lógica formal capaz de representar boa parte da matemática e linguagem natural.
Alguns vestígios da notação de Frege sobrevivem através dos símbolos derivado a partir do seu "Inhaltsstrich"´(i.e. conteúdo enfatizado) ── e "Urteilsstrich" (derivabilidade/inferência enfatizada) │. Frege usou estes símbolos em o Begriffsschrift na forma unificada ├─ para declarar que uma proposição é verdade. Em seu posterior "Grundgesetze" " ele revisa superficialmente sua interpretação sobre o símbolo ├─.
Em "Begriffsschrift" o "Definitionsdoppelstrich" (ou seja, definição de dois pontos) │├─ indica que uma proposição é uma definição. Além disso, o sinal de negação pode ser lido como uma combinação do horizontal Inhaltsstrich com um traço vertical de negação. Este símbolo de negação foi reintroduzido por Arend Heyting [1] em 1930 para distinguir intuicionismo da negação clássica. Isto também aparece na tese de doutorado de Gerhard Gentzen's.
Em o Tractatus Logico Philosophicus, Ludwig Wittgenstein presta homenagem a Frege empregando o termo Begriffsschrift como um sinônimo para o formalismo lógico.
O experimento 1892 de Frege, "Sense and reference" renega algumas das conclusões do Begriffsschrifft sobre identidade (denotados na matemática como o sinal =). Em particular, ele rejeita o "Begriffsschrift" visto que o predicado de identidade expressa uma relação entre nomes, em favor da conclusão de que isto expressa uma relação entre os objetos que são denotados por estes nomes.
Citação
"Se a tarefa da filosofia é quebrar o domínio das palavras sobre a mente humana [...], então minha notação de conceitos, a ser desenvolvida com este propósito, pode ser um instrumento útil para os filósofos [...] Eu acredito que a causa da lógica já foi avançada devido à invenção desta notação de conceitos."— Prefácio do Begriffsschrift
Referências
Outras leituras
Ligações externas
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads






 ,
,  ...
...








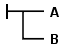

![{\displaystyle \vdash \ \ \left[\ A\rightarrow \left(B\rightarrow C\right)\ \right]\ \rightarrow \ \left[\ \left(A\rightarrow B\right)\rightarrow \left(A\rightarrow C\right)\ \right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/46233b0b84387b488948fe5ad59cef954c68fc83)
![{\displaystyle \vdash \ \ \left[\ D\rightarrow \left(B\rightarrow A\right)\ \right]\ \rightarrow \ \left[\ B\rightarrow \left(D\rightarrow A\right)\ \right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fdf8f5830ad951a8c528ea7eec78a90a79a61594)












