Szesnastkowy system liczbowy, system heksadecymalny[1] – pozycyjny system liczbowy, w którym podstawą jest liczba 16. Do zapisu liczb w tym systemie potrzebne jest szesnaście znaków (cyfr szesnastkowych).
| Liczby 0–F16 w systemie dziesiętnym, ósemkowym i dwójkowym | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0hex | = | 0dec | = | 0oct | 0 | 0 | 0 | 0 |
| 1hex | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 |
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 |
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 |
| 4hex | = | 4dec | = | 4oct | 0 | 1 | 0 | 0 |
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 |
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 |
| 7hex | = | 7dec | = | 7oct | 0 | 1 | 1 | 1 |
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 |
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 |
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 |
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | 1 |
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 |
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 |
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 |
| Fhex | = | 15dec | = | 17oct | 1 | 1 | 1 | 1 |
W najpowszechniejszym standardzie poza cyframi dziesiętnymi od 0 do 9 używa się pierwszych sześciu liter alfabetu łacińskiego: A, B, C, D, E, F (wielkich lub małych). Cyfry 0-9 mają te same wartości co w systemie dziesiętnym, natomiast litery odpowiadają następującym wartościom[2]: A = 10, B = 11, C = 12, D = 13, E = 14 oraz F = 15.
W kalkulatorach naukowych o siedmiosegmentowych wyświetlaczach LCD stosuje się następujące oznaczenia kolejnych cyfr szesnastkowych: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, C, d, E, F (b i d, zamiast B i D dla rozróżnienia wyświetlania, które wyglądają jak 8 i 0).
Istnieją również projekty ujednolicenia zapisu i wprowadzenia zupełnie nowych cyfr, przeznaczonych dla tego systemu np. propozycja nowych cyfr szesnastkowych autorstwa Bruce’a Martina (na rysunku) lub też alternatywna propozycja cyfr szesnastkowych, umożliwiająca bardziej jednolite wykorzystanie istniejących siedmiosegmentowych wyświetlaczy LCD[3].
Jak w każdym pozycyjnym systemie liczbowym, liczby zapisuje się tu jako ciągi znaków, z których każdy jest mnożnikiem kolejnej potęgi liczby stanowiącej podstawę systemu. Np. liczba zapisana w dziesiętnym systemie liczbowym jako 1000, w systemie szesnastkowym przybiera postać 3E8, gdyż:
Matematyka
W matematyce podstawę liczb zapisanych w systemach niedziesiętnych dopisuje się czasem w dolnym indeksie (zapisaną w systemie dziesiętnym). Na przykład:
Ułamki w zapisie pozycyjnym szesnastkowym:
Nauka
Wiele kalkulatorów naukowych ma dostępny dla użytkownika system szesnastkowy. Umożliwiają one zwykłe operacje na liczbach w tej postaci oraz ich konwersję do innych systemów pozycyjnych.
Elektronika
Wiele parametrów układów elektronicznych, np. kategorie urządzeń PCI, podaje się w systemie szesnastkowym.
Przykładowo – Klasa: 08h, Podklasa: 02h, Interfejs: 00h to układ odmierzający czas „8254” podobny do Intel 8253.
Adresy sprzętowe MAC urządzeń sieciowych przyznawane i podawane są w formacie szesnastkowym.
Informatyka
Szesnastkowy system liczbowy stosuje się w informatyce, w przypadku programowania niskopoziomowego, sterowania sprzętem komputerowym, wyboru adresów itp., np:
Internet
Adresy IP w wersji 6 są podawane w pozycyjnym systemie szesnastkowym np.:
- 3ffe:0902:0012:0000:0000:0000:0000:0000/48
Programowanie
Z racji budowy komputerów, w której np. adresy są potęgą liczby 2 oraz dzielą się przez 8 i 16, często stosowany jest system heksadecymalny.
Wartość pojedynczego bajta można opisać, używając tylko dwóch cyfr szesnastkowych i odwrotnie – dowolne dwie cyfry szesnastkowe można zapisać jako bajt. W ten sposób kolejne bajty można łatwo przedstawić w postaci ciągu cyfr szesnastkowych. Jednocześnie zapis 4 bitów można prosto przełożyć na jedną cyfrę szesnastkową, podczas gdy np. pozycyjny system dziesiętny nie ma własności stałej liczby bitów na cyfrę.
System szesnastkowy sprawdza się szczególnie przy zapisie dużych liczb, takich jak adresy pamięci, zakresy parametrów itp.
Konwencja matematyczna nie jest używana w informatyce. W różnych językach programowania zapis liczb szesnastkowych wygląda rozmaicie:
- C, C++, C#, Java, Python – stosuje się prefiks 0x (zero oraz x) np.
0x102f, a w ciągach tekstowych \x (ukośnik oraz x) np.\x102f. Przykładowa zamiana w języku Python wygląda tak:
hex(123) # zwróci '0x7b'
int('4f', base=16) # zwróci 79
- w Javie można też stosować szesnastkowe liczby zmiennoprzecinkowe oraz używać litery p jako wykładnika binarnego, analogicznie jak litera e używana jest w roli wykładnika dziesiętnego, np.
Komputerowy skład tekstu WWW
W języku składu stron internetowych i/lub programach edycji stron WWW:
Grafika cyfrowa, fotografia
Wiele programów do obróbki zdjęć i grafiki pozwala na wybór/wprowadzanie kodu koloru w formie szesnastkowej np. Photoshop[14] oraz GIMP.
DTP
W pełnym systemie LaTeX precyzyjny wybór koloru wygląda następująco:
- $latex niebieskie-slowo&bg=cc0000&fg=0000F0$
Życie codzienne
W 1863 zaproponowano nowe cyfry oraz standard zapisu i pomiaru czasu (zegar) oraz lokalizacji (kompas) w systemie pozycyjnym szesnastkowym.
Współczesny projekt standardu pomiaru czasu w systemie pozycyjnym szesnastkowym
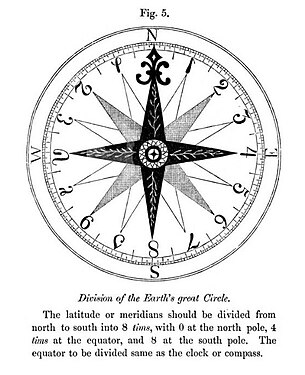
Projekt kompasu zaproponowany w XIX wieku przez Nystroma w systemie pozycyjnym szesnastkowym
Przypisy
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
