Ampères sirkulasjonslov

Ampères sirkulasjonslov er en naturlov som forbinder magnetfeltet rundt en lukket kurve med størrelsen til den elektriske strømmen som går gjennom kurven så lenge denne strømmen er konstant. Loven er oppkalt etter den franske fysiker André-Marie Ampère som var den som først utforsket på en systematisk måte sammenhengen mellom elektriske strømmer og magnetfelt.

En elektrisk strøm I omgir seg med et sirkulært, magnetisk felt B.

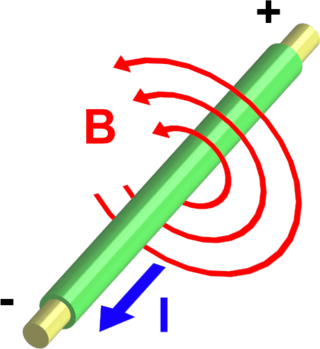
I det generelle tilfellet når strømmen varierer med tiden, viste Maxwell hvordan loven kan utvides. Den omtales da som Maxwells fjerde ligning.

Gitt en vilkårlig kurve C  i et magnetfelt B = B(r), kan Ampères sirkulasjonslov skrives som det lukkete linjeintegralet

${\displaystyle \oint _{\!C}\mathbf {B} \cdot d\mathbf {s} =\mu _{0}I}$

hvor I er den totale, elektriske strømmen som kurven omslutter og μ₀  er den magnetiske konstanten i SI-systemet. På denne formen tilsvarer loven Gauss' lov i elektrostatikken og kan under spesielle forhold benyttes til å beregne magnetfeltet direkte fra den gitte strømmen.

Alternativt kan loven skrives på differensiell form ved bruk av Stokes' teorem som

${\displaystyle {\boldsymbol {\nabla }}\times \mathbf {B} =\mu _{0}\mathbf {J} }$

hvor J = J(r) er den konstante strømtettheten i punktet r. For praktiske beregninger kan ikke denne fundamentale formuleringen vanligvis benyttes. Derimot kan magnetfeltet i det generelle tilfellet da finnes fra Biot-Savarts lov som er en ekvivalent utgave av Ampères sirkulasjonslov.

Historie

På den tiden Ørsted i 1820 oppdaget for første gang at en strømførende ledning kunne påvirke en nærliggende kompassnål, hadde man liten forståelse av hva en elektrisk strøm besto av. Han omtalte derfor den magnetiske virkningen til strømmen som en elektrisk konflikt som artet seg på en sirkulær måte rundt den strømførende ledningen. Resultatet av hans eksperiment er nå oppsummert i Ørsteds lov.

Det var Ampère som noen måneder senere gikk i gang med mer presise målinger av disse nye, magnetiske effektene. Han eliminerte effekten av det jordmagnetiske feltet og fant at kompassnålen utenfor en rett, strømførende ledningen stilte seg inn vinkelrett til denne. I samme forbindelse viste han også at strømmen gjennom batteriet ga tilsvarende, magnetiske effekter som utenfor ledningen og sluttet derav at strømmen gikk i en lukket, elektrisk krets. Det er denne første, systematiske utforskning av den elektriske strømmen som har fått Ampères navn knyttet til dens måleenhet ampere i SI-systemet.^[1]

Hans sirkulasjonsteorem stammer fra disse undersøkelsene som også viste at den magnetiske kraften mellom to ledninger avtok omvendt proporsjonalt med avstanden mellom dem. Teoremet ble matematisk formulert av Maxwell først førti år senere og da utvidet til å omhandle også tidsvariable felt og strømmer.

Anvendelser

Ørsted og Ampère fant at den magnetiske kraften var sirkulært fordelt rundt en uendelig, rett strømførende leder. Ved å anta at denne kraften er proporsjonal med et magnetisk felt, vil dette da være konstant rundt en sirkel med sentrum i lederen og rettet tangensielt til denne. Er strømmen i ledningen I og har sirkelen radius r, gir da sirkulasjonsteoremet på integralform at 2π rB = μ₀I. Styrken til magnetfeltet utenfor ledningen varierer derfor som

${\displaystyle B={\mu _{0}I \over 2\pi r}}$

og summerer opp Ampères eksperimentelle resultat. Feltet varierer med avstanden på samme måte som det elektriske feltet fra en linjeladning.^[2]

Har ledningen et sirkulært tverrsnitt med radius a, kan man også benytte sirkulasjonsteoremet til å beregne magnetfelt inni den. Da strømtettheten gjennom den da er J = I /πa², er den totale strømmen som går gjennom en sirkel med radius r < a lik med I_r = I (r/a)². Velger man en slik sirkel som integrasjonsvei, sier teoremet igjen at 2π rB = μ₀I_r. Inni lederen går derfor magnetfeltet også i sirkler, men med styrken

${\displaystyle B={\mu _{0}Ir \over 2\pi a^{2}},\;\;\;r\leq a}$

I sentrum av lederen er det null og går ved overflaten r = a kontinuerlig over i verdien det har utenfor ledningen.

At disse anvendelsene er såpass enkle, skyldes den spesielle geometrien i problemet som tilsier at feltet er konstant langs sirkelen som brukes ved linjeintegrasjonen. I mer generelle situasjoner kan man ikke benytte slike forenklinger og sirkulasjonsteoremet lar seg derfor vanskelig benytte. Et unntak er en konstant strømtetthet K (A/m) i et plan. Velges dette å være z-planet med strømmen i y-retning, vil det resulterende magnetfeltet være normalt både til denne og planet. Derfor vil det være parallelt med x-aksen over og under z-planet, men motsatt rettet. For denne situasjonen kan man da velge en integrasjonsvei i sirkulasjonsteoremet som er et rektangel med sider over og under planet langs x-aksen med lengde L. De to andre sidene i rektanglet vil ikke bidra til integralet da de står vinkelrett på feltet. Teoremet gir da at 2LB = μ₀KL. Det resulterende feltet blir dermed

${\displaystyle B={\mu _{0}K \over 2}}$

og er uavhengig av avstanden fra planet. Dette er analogt med det elektriske feltet utenfor et uniformt ladet plan.

Generaliseringer

På midten av 1800-tallet tok Thomson opp studiet av magnetiske felt i materialer. De kan ha en magnetisering M som var blitt innført av Poisson noen tiår tidligere. Hvis denne varierte i rommet, ville det gi opphav til en stasjonær, men bundet strømtetthet J_m = ∇ × M  i materialet.^[1] I sirkulasjonsteoremet vil da den totale strømtettheten J_tot = J + J_m  hvor J er den fri strømmen, bestemme magnetfeltet der. Thomson fant det da hensiktsmessig å innføre et nytt magnetfelt H som kun skyldes denne. Ved å sette

${\displaystyle \mathbf {B} =\mu _{0}(\mathbf {H} +\mathbf {M} ),}$

vil da dette nye feltet kunne bestemmes fra den modifiserte versjonen

${\displaystyle {\boldsymbol {\nabla }}\times \mathbf {H} =\mathbf {J} }$

av Ampères sirkulasjonsteorem. Disse ligningene er de grunnleggende for magnetostatikken som beskriver magnetiske felt i materialer under stasjonære forhold.^[3]

Vel ti år senere begynte Maxwell å formulere sine elektromagnetiske ligninger for felt som også forandrer seg med tiden. Dette lykkes han først med ved å innføre en forskyvningsstrøm J_D = ∂D/∂t  hvor D er det elektriske forskyvningsfeltet. Det opprinnelige teoremet til Ampère fikk dermed sin endelige form

${\displaystyle {\boldsymbol {\nabla }}\times \mathbf {H} =\mathbf {J} +{\partial \mathbf {D} \over \partial t}}$

og kalles ofte for Maxwell-Ampères sirkulasjonslov. Da divergensen til curl på venstre side av ligningen er null, er denne formuleringen nå også i overensstemmelse med kontinuitetsligningen for elektrisk strøm da ∇⋅D = ρ.

Topologisk sammenheng

Ampères sirkulasjonsteorem inneholder et dypt, topologisk resultat. I deler av rommet hvor det ikke er noen elektriske strømmer, er ∇ × H = 0. Magnetfeltet B = μ₀H kan derfor skrives som gradienten av et skalært potensial, H = - ∇ Ψ. Ved en integrasjon langs en kurve som forbinder to punkt P₁ og P₂ i rommet, har man da at

${\displaystyle \int _{P_{1}}^{P_{2}}\mathbf {H} \cdot d\mathbf {s} =\Psi (P_{1})-\Psi (P_{2})}$

Selv om Ampère ikke tenkte på magnetiske krefter formidlet av et felt, viste han at en lukket strømsløyfe kunne tilordnes en matematisk størrelse som han kalte for en direktrise.^[4] Den tilsvarer magnetfeltet H og kunne uttrykkes som gradienten av skalarpotensialet

${\displaystyle \Psi =-I{\Omega \over 4\pi }}$

hvor Ω er den romvinkelen som strømsløyfen sees under fra et gitt punkt P. Beveger dette punktet seg bort et stykke, avtar romvinkelen. Hvis det så flytter seg tilbake til utgangspunket, gjerne langs en annen vei, vil vinkelen vokse og komme tilbake til den opprinnelige verdien i P.

Men det er tilfelle kun når punktet i sin lukkete bevegelse ikke omslutter noen del av den strømførende ledning. Dette blir tydelig hvis man betrakter en plan strømsløyfe og et punkt P₁ som ligger like under dette planet. Da er Ω₁ = - 2π  hvor fortegnet er bestemt ved strømretningen. Hvis nå dette punktet beveger seg bort fra sløyfen, vokser romvinkelen Ω og blir null hvis punktet flytter seg til et punkt i planet utenfor sløyfen. Fortsetter så denne bevegelsen tilbake mot oversiden til sløyfen, vil Ω bli positiv og fortsette å vokse. Og i et punkt P₂ på oversiden av sløyfen, men akkurat i samme posisjon som P₁, vil romvinkelen ha blitt til Ω₂ = 2π. Punktet har da beskrevet en lukket kurve C og linjeintegralet fra P₁ til P₂ blir

${\displaystyle \oint _{C}\!\mathbf {H} \cdot d\mathbf {s} ={I \over 4\pi }{\Big (}2\pi -(-2\pi ){\Big )}=I}$

Hadde punktet fortsatt sin bevegelse en slik runde til, ville integralet ha gitt to ganger strømmen som kurven C omslutter. Integralet teller derfor hvor mange ganger den lukkete integrasjonskurven C omslutter strømsløyfen. I topologien kalles dette for kurvenes lenketall som sier hvor mange ganger den ene tvinner seg om den andre.

Denne sammenhengen ble først undersøkt av Gauss i 1833 i hans matematiske beskrivelse av magnetfeltet.^[5] Er den lukkete integrasjonskurven C₁ og strømsløyfen C₂ og man uttrykker magnetfeltet skapt av denne ved Biot-Savarts lov, så er derfor lenketallet m gitt ved det doble linjeintegralet

${\displaystyle m=\oint _{\!C_{1}}\!\oint _{\!C_{2}}\!\ {(d\mathbf {s} _{1}\times d\mathbf {s} _{2})\cdot (\mathbf {r} _{1}-\mathbf {r} _{2}) \over 4\pi |\mathbf {r} _{1}-\mathbf {r} _{2}|^{3}}}$

etter å ha benyttet egenskapen a⋅(b × c) = (a × b)⋅c til det skalære trippelproduktet i telleren. Denne størrelsen ble gjenoppdaget av Maxwell i 1867 og er nå en sentral del av moderne knuteteori.^[6]

Referanser

1. O. Darrigol, Electrodynamics from Ampère to Einstein, Oxford University Press, Oxford (2000). ISBN 0-19-850593-0.
2. H.D. Young og R.A. Freedman, University Physics, Addison-Wesley, New York (2008). ISBN 978-0-321-50130-1.
3. A. Zangwill, Modern Electrodynamics, Cambridge University Press, Cambridge (2013). ISBN 978-0-521-89697-9.
4. R.A.R. Tricker, Early Electrodynamics, Pergamon Press, London (1965).
5. E.T. Whittaker, A History of the Theories of Aether and Electricity, Longman, Green and Co, London (1910).
6. R.L. Ricca and B. Nipoti, Gauss' linking number revisited, Journal of Knot Theory and Its Ramifications 20(10), 1325–1343 (2011).